NCERT Solutions for Class 7 Maths Chapter 8 Working With Fractions
We frequently use fractions in our everyday lives. For example, if you cut an apple into 4 pieces and give one piece to your friend, then your friend has $\frac14$ of the apple. In another example, if you take 30 minutes to do the job, then you have taken $\frac12$ hours to do it. In Class 7 Maths NCERT Chapter 8, 'Working With Fractions', students will learn how to add, subtract, multiply, divide, and compare fractions easily. There are many occasions where using factions becomes essential for us. Therefore, it is important to understand this chapter with a proper understanding and clarity, and this is where the NCERT Solutions for Class 7 Maths come into play.
This Story also Contains
- NCERT Solutions for Class 7 Maths Chapter 8 Working With Fractions: Download Free PDF
- NCERT Solutions for Class 7 Maths Chapter 8 Working With Fractions (Exercise)
- NCERT Working With Fractions Class 7 Maths Chapter 8: Topics
- Class 7 Maths Chapter 8 Working With Fractions Solutions: Extra Question
- NCERT Solutions for Class 7 Maths Chapter 8 Working with Fractions: Notes
- Why are Class 7 Maths Chapter 8 Working with Fractions Question Answers Important?
- NCERT Solutions for Class 7 Mathematics Chapter Wise
- NCERT Books and NCERT Syllabus

These NCERT Solutions provide detailed and step-by-step explanations for the students. With the help of these solutions, they can practice problems on their own, verify their answers, and strengthen their weak areas that need improvement. This article will also clear their doubts and provide them with a proper understanding of the chapter's concepts. These NCERT Solutions for Class 7 are trustworthy and reliable, as they are created by subject matter experts at Careers360, making them an essential resource for exam preparation. For detailed solutions, complete syllabus notes, and a free PDF download, refer to this NCERT article.
NCERT Solutions for Class 7 Maths Chapter 8 Working With Fractions: Download Free PDF
Careers360 brings you NCERT Class 7 Maths Chapter 8 Working With Fractions solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 7 Maths Chapter 8 Working With Fractions (Exercise)
NCERT Class 7 Maths Chapter 8 Working With Fractions question answers with detailed explanations are provided below.
| Working With Fractions Class 7 Question Answers Page number: 176 Number of Questions: 5 |
Figure it Out
Question 1: Tenzin drinks $\frac{1}{2}$ glass of milk every day. How many glasses of milk does he drink in a week? How many glasses of milk did he drink in the month of January?
Solution:
Glass of milk drank every day $=\frac{1}{2}$
Glasses of milk drank in a week $=\frac{1}{2} \times 7=\frac{7}{2}$
Days in month of January = 31
Glasses of milk drank in month of January $=31 \times \frac{1}{2}=\frac{31}{2}=15 \frac{1}{2}$.
Question 2: A team of workers can make 1 km of a water canal in 8 days. So, in one day, the team can make ___ km of the water canal. If they work 5 days a week, they can make ___ km of the water canal in a week.
Solution:
The length of the canal made by workers in 8 days $=1 \mathrm{~km}$
The length of canal made by workers in 1 day $=\frac{1}{8} \mathrm{~km}$
By working 5 days a week, the length of the canal made by workers $=5 \times \frac{1}{8}=\frac{5}{8} \mathrm{~km}$.
Question 3: Manju and two of her neighbours buy 5 litres of oil every week and share it equally among the 3 families. How much oil does each family get in a week? How much oil will one family get in 4 weeks?
Solution:
Amount of oil shared by 3 families in a week = 5 litres
Amount of oil one family got in a week $=\frac{5}{3}$ litres
Amount of oil one family got in 4 weeks $=4 \times \frac{5}{3}=\frac{20}{3}=6 \frac{2}{3}$ litres.
Question 4: Safia saw the Moon setting on Monday at 10 pm. Her mother, who is a scientist, told her that every day the Moon sets $\frac{5}{6}$ hours later than the previous day. How many hours after 10 pm will the moon set on Thursday?
Solution:
Number of days from Monday to Thursday $=3$
Delay in moon setting time per day $=\frac{5}{6}$ hour
Delay in moon setting time over 3 days $=3 \times \frac{5}{6}$ hour $=\frac{5}{2}=2.5$ hours
Thus, the Moon will set 2.5 hours or 2 hours and 30 minutes after 10 PM on Thursday.
Question 5: Multiply and then convert it into a mixed fraction:
(a) $7 \times \frac{3}{5}$ (b) $4 \times \frac{1}{3}$ (c) $\frac{9}{7} \times 6$ (d) $\frac{13}{11} \times 6$
Solution:
(a) $7 \times \frac{3}{5}=\frac{21}{5}=4 \frac{1}{5}$
(b) $4 \times \frac{1}{3}=\frac{4}{3}=1\frac{1}{3}$
(c) $\frac{9}{7} \times 6=\frac{54}{7}=7\frac{5}{7}$
(d) $\frac{13}{11} \times 6=\frac{78}{11}=7\frac{1}{11}$
| Working With Fractions Class 7 Question Answers Page number: 180 Number of Questions: 2 |
Figure it Out
Question 1: Find the following products. Use a unit square as a whole for representing the fractions:
(a) $\frac{1}{3} \times \frac{1}{5}$ (b) $\frac{1}{4} \times \frac{1}{3}$ (c) $\frac{1}{5} \times \frac{1}{2}$ (d) $\frac{1}{6} \times \frac{1}{5}$
Solution:
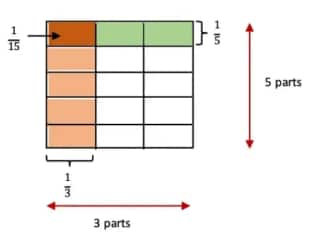
(a) $\frac{1}{3} \times \frac{1}{5}$
Unit square divided into 3 rows and 5 columns = 15 parts.
1 part shaded $=\frac{1}{15}$. Thus, $\frac{1}{3}×\frac{1}{5}=\frac{1}{15}$
(b) $\frac{1}{4} \times \frac{1}{3}$
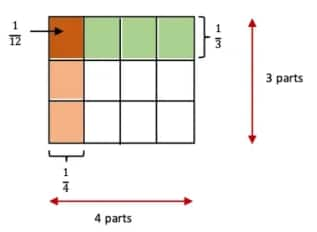
A unit square divided into 4 rows and 3 columns = 12 parts.
1 part shaded $=\frac{1}{12}$. Thus, $\frac{1}{4}×\frac{1}{3}=\frac{1}{12}$
(c) $\frac{1}{5} \times \frac{1}{2}$
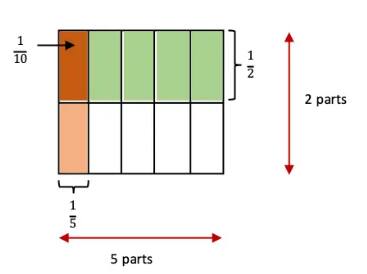
A unit square divided into 5 rows and 2 columns = 10 parts.
1 part shaded $=\frac{1}{10}$. Thus, $\frac{1}{5}×\frac{1}{2}=\frac{1}{10}$
(d) $\frac{1}{6} \times \frac{1}{5}$
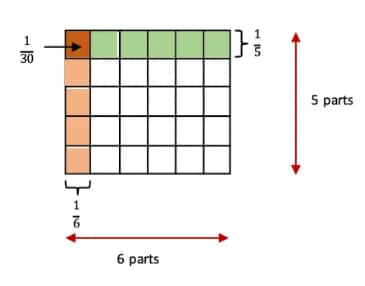
A unit square divided into 6 rows and 5 columns = 30 parts.
1 part shaded $=\frac{1}{30}$. Thus, $\frac{1}{6}×\frac{1}{5}=\frac{1}{30}$
Question 2: Find the following products. Use a unit square as a whole for representing the fractions and carrying out the operations.
(a) $\frac{2}{3} \times \frac{4}{5}$ (b) $\frac{1}{4} \times \frac{2}{3}$ (c) $\frac{3}{5} \times \frac{1}{2}$ (d) $\frac{4}{6} \times \frac{3}{5}$
Solution:
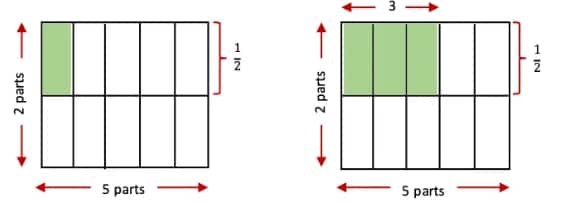
(a) $\frac{2}{3} \times \frac{4}{5}$
First, the whole is divided into 5 rows and 3 columns, creating (5 × 3) = 15 equal parts.
The value we get by dividing $\frac{4}{5}$ into 3 equal parts is $\frac{4}{3 \times 5}$.
Thus, we multiply this result by 2 to get the product. This is $\frac{2 \times 4}{3 \times 5}$.
So, $\frac{2}{3} \times \frac{4}{5}=\frac{2 \times 4}{3 \times 5}=\frac{8}{15}$.
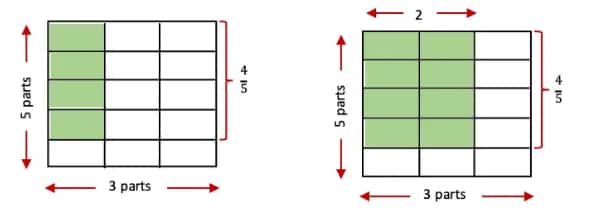
(b) $\frac{1}{4} \times \frac{2}{3}$
First, the whole is divided into 3 rows and 4 columns, creating (3 × 4) = 12 equal parts.
The value we get by dividing $\frac{2}{3}$ into 4 equal parts is $\frac{2}{4 \times 3}$.
So, $\frac{1}{4} \times \frac{2}{3}=\frac{1 \times 2}{4 \times 3}=\frac{2}{12}$.
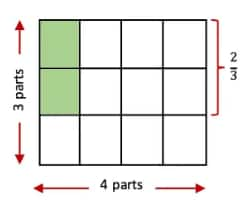
(c) $\frac{3}{5} \times \frac{1}{2}$
First, the whole is divided into 2 rows and 5 columns, creating (2 × 5) = 10 equal parts. The value we get by dividing $\frac{1}{2}$ into 5 equal parts is $\frac{1}{5 \times 2}$.
Thus, we multiply this result by 3 to get the product. This is $\frac{3 \times 1}{5 \times 2}$.
So, $\frac{3}{5} \times \frac{1}{2}=\frac{3 \times 1}{5 \times 2}=\frac{3}{10}$.
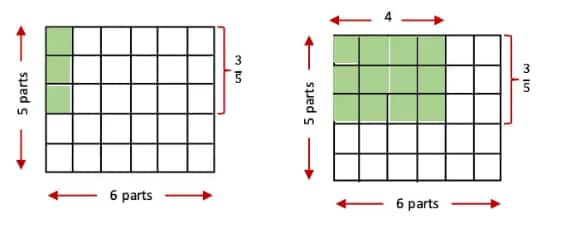
(d) $\frac{4}{6} \times \frac{3}{5}$
First, the whole is divided into 5 rows and 6 columns, creating (5 × 6) = 30 equal parts.
The value we get by dividing $\frac{3}{5}$ into 6 equal parts is $\frac{3}{6 \times 5}$.
Thus, we multiply this result by 4 to get the product. This is $\frac{4 \times 3}{6 \times 5}$.
So, $\frac{4}{6} \times \frac{3}{5}=\frac{4 \times 3}{6 \times 5}=\frac{12}{30}$.
| Working With Fractions Class 7 Question Answers Page number: 183 Number of Questions: 5 |
Figure it Out
Question 1: A water tank is filled from a tap. If the tap is open for 1 hour, $\frac{7}{10}$ of the tank gets filled. How much of the tank is filled if the tap is open for
(a) $\frac{1}{3}$ hour $\qquad$
(b) $\frac{2}{3}$ hour $\qquad$
(c) $\frac{3}{4}$ hour $\qquad$
(d) $\frac{7}{10}$ hour $\qquad$
(e) For the tank to be full, how long should the tap be running?
Solution:
Part of the tank filled in 1 hour $=\frac{7}{10}$
(a) Part of the tank filled in $\frac{1}{3}$ hour $=\frac{1}{3} \times \frac{7}{10}=\frac{7}{30}$
(b) Part of the tank filled in $\frac{2}{3}$ hour $=\frac{2}{3} \times \frac{7}{10}=\frac{14}{30}=\frac{7}{15}$
(c) Part of the tank filled in $\frac{3}{4}$ hour $=\frac{3}{4} \times \frac{7}{10}=\frac{21}{40}$
(d) Part of the tank filled in $\frac{7}{10}$ hour $=\frac{7}{10} \times \frac{7}{10}=\frac{49}{100}$
(e) Part of the tank filled in 1 hour $=\frac{7}{10}$
⇒ Time required to fill $\frac{7}{10}$ of a tank $=1$ hour
Time required to fill 1 tank $=1 \div \frac{7}{10}=1 \times \frac{10}{7}=\frac{10}{7}$ hours $=1 \frac{3}{7}$ hours.
Question 2: The government has taken $\frac{1}{6}$ of Somu’s land to build a road. What part of the land remains with Somu now? She gives half of the remaining part of the land to her daughter, Krishna and $\frac{1}{3}$ of it to her son, Bora. After giving them their shares, she kept the remaining land for herself.
(a) What part of the original land did Krishna get?
(b) What part of the original land did Bora get?
(c) What part of the original land did Somu keep for herself?
Solution:
Part of Somu's land acquired by the government $=\frac{1}{6}$
Somu's original land $=1-\frac{1}{6}=\frac{6-1}{6}=\frac{5}{6}$
(a) Part of the land given to Krishna $=\frac{1}{2}$ of original land $=\frac{1}{2} \times \frac{5}{6}=\frac{5}{12}$
(b) Part of the land given to Bora $=\frac{1}{3}$ of original land $=\frac{1}{3} \times \frac{5}{6}=\frac{5}{18}$
(c) Part of the land Somu kept for herself $=\frac{5}{6}-\left(\frac{5}{12}+\frac{5}{18}\right)$
$=\frac{5}{6}-\left(\frac{3 \times 5+5 \times 2}{36}\right)$
$=\frac{5}{6}-\left(\frac{15+10}{36}\right)$
$=\frac{5}{6}-\left(\frac{25}{36}\right)$
$=\frac{6 \times 5-25}{36}$
$=\frac{30-25}{36}=\frac{5}{36}$
Question 3: Find the area of a rectangle of sides $3 \frac{3}{4} \mathrm{ft}$ and $9 \frac{3}{5} \mathrm{ft}$.
Solution:
Area of rectangle $=(3 \frac{3}{4} \times 9 \frac{3}{5}) \mathrm{ ft}=(\frac{15}{4} \times \frac{48}{5}) \mathrm{ ft}=\frac{720}{20}\mathrm{ ft}=36 \text{ ft}$
Question 4: Tsewang plants four saplings in a row in his garden. The distance between two saplings is $\frac{3}{4} \mathrm{~m}$. Find the distance between the first and last sapling.
Solution:
Number of saplings in a row in the garden $=4$
Distance between two saplings $=\frac{3}{4}$
Distance between first and last sapling $=\frac{3}{4}+\frac{3}{4}+\frac{3}{4}=\frac{3+3+3}{4}=\frac{9}{4} \mathrm{~m}=2 \frac{1}{4} \mathrm{~m}$.
Question 5: Which is heavier: $\frac{12}{15}$ of 500 grams or $\frac{3}{20}$ of 4 kg?
Solution:
$\frac{12}{15} \times 500\mathrm{~g}=\frac{4}{5} \times 500\mathrm{~g}=400$ grams.
$\frac{3}{20} \times 4 \mathrm{~kg}=\frac{3}{20} \times 4000 \mathrm{~g}=600$ grams.
Since 600 g is heavier than 400 g
Therefore, $\frac{3}{20}$ of 4 kg is heavier than $\frac{12}{15}$ of 500 grams.
|
Working With Fractions Class 7 Question Answers |
Question 1: Evaluate the following:
|
|
|
|
|
|
|
|
| |
|
|
|
|
Solution:
| Expression |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Question 2: For each of the questions below, choose the expression that describes the solution. Then simplify it.
(a) Maria bought 8 m of lace to decorate the bags she made for school. She used $\frac{1}{4} \mathrm{~m}$ for each bag and finished the lace. How many bags did she decorate?
(i) $8 \times \frac{1}{4}$
(ii) $\frac{1}{8} \times \frac{1}{4}$
(iii) $8 \div \frac{1}{4}$
(iv) $\frac{1}{4} \div 8$
Solution:
Maria bought 8 m of lace to decorate the bags she made for school.
So, total lace = 8 m
One bag took $\frac14$ m of lace.
So, total bags she decorated $=8\div\frac14=\frac{8}{\frac14}=8\times4=32$
Hence, the correct answer is option (iii).
Question 2: For each of the questions below, choose the expression that describes the solution. Then simplify it.
(b) $\frac{1}{2}$ meter of ribbon is used to make 8 badges. What is the length of the ribbon used for each badge?
(i) $8 \times \frac{1}{2}$
(ii) $\frac{1}{2} \div \frac{1}{8}$
(iii) $8 \div \frac{1}{2}$
(iv) $ \frac{1}{2} \div 8$
Solution:
$\frac{1}{2}$ meter of ribbon is used to make 8 badges.
So, for each bandage, the amount of ribbon used
$=\frac12\div 8 = \frac 12 \times\frac18 =\frac1{16}$
Hence, the correct answer is option (iv).
Question 2: For each of the questions below, choose the expression that describes the solution. Then simplify it.
(c) A baker needs $\frac{1}{6} \mathrm{~kg}$ of flour to make one loaf of bread. He has 5 kg of flour. How many loaves of bread can he make?
(i) $5 \times \frac{1}{6}$
(ii) $\frac{1}{6} \div 5$
(iii) $5 \div \frac{1}{6}$
(iv) $ 5 \times 6$
Solution:
A baker needs $\frac{1}{6} \mathrm{~kg}$ of flour to make one loaf of bread.
Total flour = 5 kg
So, the number of bread made $=5\div \frac16=5\times6=30$
Hence, the correct answer is option(iii).
Question 3: If $\frac{1}{4} \mathrm{~kg}$ of flour is used to make 12 rotis, how much flour is used to make 6 rotis?
Solution:
12 rotis takes $\frac{1}{4} \mathrm{~kg}$ of flour to be made.
So, 6 rotis will take half the amount, as the number of rotis is also halved.
So, required amount of flour $=\frac14\div 2=\frac14\times\frac12=\frac18$
Hence, the correct answer is $\frac18$.
Question 4: Pạtiganita, a book written by Sridharacharya in the 9th century CE, mentions this problem: "Friend, after thinking, what sum will be obtained by adding together $1 \div \frac{1}{6}, 1 \div \frac{1}{10}, 1 \div \frac{1}{13}, 1 \div \frac{1}{9}$, and $1 \div \frac{1^{\prime \prime}}{2}$. What should the friend say?
Solution:
$1 \div \frac{1}{6}=1\times6=6$
$1 \div \frac{1}{10}=1\times10=10$
$1 \div \frac{1}{13}=1\times13=13$
$1 \div \frac{1}{9}=1\times9=9$
$1 \div \frac12=1\times2=2$
So, total = 6 + 10 + 13 + 9 + 2 = 40
Hence, the correct answer is 40.
Question 5: Mira is reading a novel that has 400 pages. She read $\frac{1}{5}$ of the pages yesterday and $\frac{3}{10}$ of the pages today. How many more pages does she need to read to finish the novel?
Solution:
Total pages of the novel = 400
$\frac{1}{5}$ of the pages $= \frac15\times400=80$ pages
$\frac{3}{10}$ of the pages $=\frac3{10}\times400=120$ pages
$\therefore$ Pages left to read $=400-80-120=200$ pages
Hence, the correct answer is 200 pages.
Question 6: A car runs 16 km using 1 litre of petrol. How far will it go using $2 \frac{3}{4}$ litres of petrol?
Solution:
Using 1 litre of petrol, a car runs 16 km.
So, using $2 \frac{3}{4}=\frac{11}4$ litres of petrol, the car will run
$=\frac{11}4\times16=44$ km
Hence, the correct answer is 44 km.
Question 7: Amritpal decides on a destination for his vacation. If he takes a train, it will take him $5 \frac{1}{6}$ hours to get there. If he takes a plane, it will take him $\frac{1}{2}$ hour. How many hours does the plane save?
Solution:
The train takes $5 \frac{1}{6}$ hours to get to the destination.
But the plane will take him $\frac{1}{2}$ hour.
$\therefore$ Hours saved $=5 \frac{1}{6}-\frac12=\frac{31}6-\frac12=\frac{28}6=\frac{14}3$ hours
Hence, the correct answer is $\frac{14}3$ hours.
Question 8: Mariam's grandmother baked a cake. Mariam and her cousins finished $\frac{4}{5}$ of the cake. The remaining cake was shared equally by Mariam's three friends. How much of the cake did each friend get?
Solution:
Let the total cake be 1.
Mariam and her cousins finished $\frac{4}{5}$ of the cake.
So, remaining cake $=1-\frac15=\frac45$
The remaining cake was shared equally by Mariam's three friends.
So, share of every friend $=\frac45 \div 3=\frac45\times \frac13=\frac4{15}$th of the cake
Hence, the correct answer is $\frac4{15}$.
Question 9: Choose the option(s) describing the product of $\left(\frac{565}{465} \times \frac{707}{676}\right)$ :
(a) $>\frac{565}{465}$
(b) $<\frac{565}{465}$
(c) $>\frac{707}{676}$
(d) $<\frac{707}{676}$
(e) $>1$
(f) $<1$
Solution:
Here, 565 > 465
So, $\frac{565}{465}>1$
Similarly, 707 > 676
So, $\frac{707}{676}>1$
When you multiply two fractions that are both slightly greater than 1, the result will be greater than 1.
So, $\left(\frac{565}{465} \times \frac{707}{676}\right)>1$
Since both $\frac{565}{465}$ and $\frac{707}{676}$ are greater than 1, their product will be greater than either fraction individually.
Therefore, the product is:
- Greater than $\frac{565}{465}$ (a),
- Greater than $\frac{707}{676}$ (c),
- Greater than 1 (e).
Hence, the correct answer is options (a), (c), and (e).
Question 10: What fraction of the whole square is shaded?
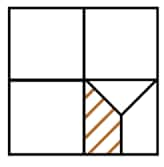
Solution:
Here, four small squares of equal size.
Now, consider the small square.
If you divide it into 8 equal triangles, the shaded part will occupy 3 triangles.
So, the shaded part is $\frac38$th of the small square.
$\therefore$ the shaded part is $\frac38\times\frac14=\frac3{32}$ part of the big square
Hence, the correct answer is $\frac3{32}$ part.
Question 11: A colony of ants set out in search of food. As they search, they keep splitting equally at each point (as shown in Fig. 8.7) and reach two food sources, one near a mango tree and another near a sugarcane field. What fraction of the original group reached each food source?
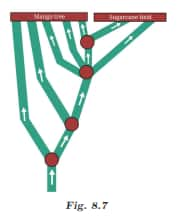
Solution:
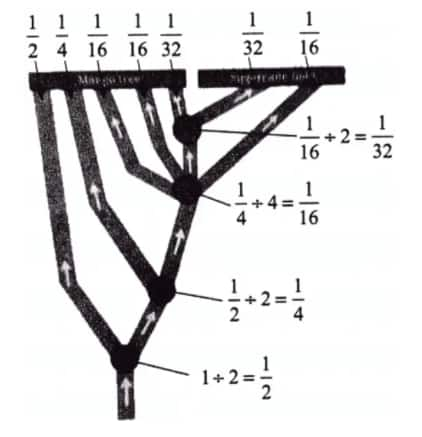
Let the total ants at the start be 1.
At the first point, ants split into two ways.
So, $\frac12$ the ants go either way.
In the next intersection, the fraction of ants on each way $=\frac12 \div 2=\frac14$
At the third point, ants split in half again.
So, fraction of ants at each way $=\frac14 \div 4=\frac1{16}$
At the next point, ants split into 2 ways.
So fraction of ants at each way $=\frac1{16} \div 2=\frac1{32}$
Hence, a fraction of ants at the mango tree is:
$\frac12+\frac14+\frac1{16}+\frac1{16}+\frac1{32}=\frac{29}{32}$
The fraction of ants near the sugarcane field is:
$\frac1{32}+\frac1{16}=\frac3{32}$
Question 12: What is
$1-\frac{1}{2}?$
$\begin{aligned} & \left(1-\frac{1}{2}\right) \times\left(1-\frac{1}{3}\right) ? \\ & \left(1-\frac{1}{2}\right) \times\left(1-\frac{1}{3}\right) \times\left(1-\frac{1}{4}\right) \times\left(1-\frac{1}{5}\right) ? \\ & \left(1-\frac{1}{2}\right) \times\left(1-\frac{1}{3}\right) \times\left(1-\frac{1}{4}\right) \times\left(1-\frac{1}{5}\right) \times\left(1-\frac{1}{6}\right)\\& \times\left(1-\frac{1}{7}\right) \times\left(1-\frac{1}{8}\right) \times\left(1-\frac{1}{9}\right) \times\left(1-\frac{1}{10}\right) ?\end{aligned}$
Make a general statement and explain.
Solution:
Expression 1:
$1-\frac{1}{2}=\frac{2}{2}-\frac{1}{2}=\frac{1}{2}$
Expression 2:
$\left(1-\frac{1}{2}\right) \times\left(1-\frac{1}{3}\right)$
$=\frac12\times\frac23$
$=\frac13$
Expression 3:
$\left(1-\frac{1}{2}\right) \times\left(1-\frac{1}{3}\right) \times\left(1-\frac{1}{4}\right)$
$=\frac12\times\frac23\times\frac34$
$=\frac14$
Expression 4:
$\left(1-\frac{1}{2}\right) \times\left(1-\frac{1}{3}\right) \times\left(1-\frac{1}{4}\right) \times\left(1-\frac{1}{5}\right) \times\left(1-\frac{1}{6}\right)$
$ \times\left(1-\frac{1}{7}\right) \times\left(1-\frac{1}{8}\right) \times\left(1-\frac{1}{9}\right) \times\left(1-\frac{1}{10}\right)$
$=\frac12\times\frac23\times\frac34\times\frac45\times\frac56\times\frac67\times\frac78\times\frac89\times\frac9{10}$
$=\frac1{10}$
The general statement is that multiplying the terms $\left(1-\frac{1}{k}\right)$ for $k=2,3,4, \ldots, n$ results in $\frac{1}{n}$.
NCERT Working With Fractions Class 7 Maths Chapter 8: Topics
The important topics that are covered in NCERT Class 7 Maths Chapter 8, Working With Fractions, are:
- Multiplication of Fractions
- Connection between the Area of a Rectangle and Fraction Multiplication
- Simplifying to Lowest Form
- Order of Multiplication
- Division of Fractions
- Some Problems Involving Fractions
Class 7 Maths Chapter 8 Working With Fractions Solutions: Extra Question
Question:
Kushal has $\frac{3}{4}$ of a cake. He wants to divide it equally among $\frac{1}{2}$ of his friends. How much cake will each friend get?
Solution:
So, the amount of cake Kushal's friends will get is:
$\frac{3}{4} \div \frac{1}{2}$
$=\frac{3}{4} \times \frac{2}{1}$
$=\frac64$
$=\frac32$
$=1\frac12$
Hence, the correct answer is $1\frac12$.
NCERT Solutions for Class 7 Maths Chapter 8 Working with Fractions: Notes
Careers360 has prepared these Class 7 Working with Fractions Notes to make your revision smoother and faster. Additionally, these notes will help students understand the Working with Fractions NCERT solutions and solve them independently from next time.
Fractions
Fractions can be defined as a part of a whole. When one unit is divided into several equal parts, each part is called a fractional unit. The fractional units are $\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \ldots, \frac{1}{10}, \ldots, \frac{1}{50}, \ldots, \frac{1}{100}$, etc. We also sometimes refer to fractional units as unit fractions.
Multiplication of Fractions
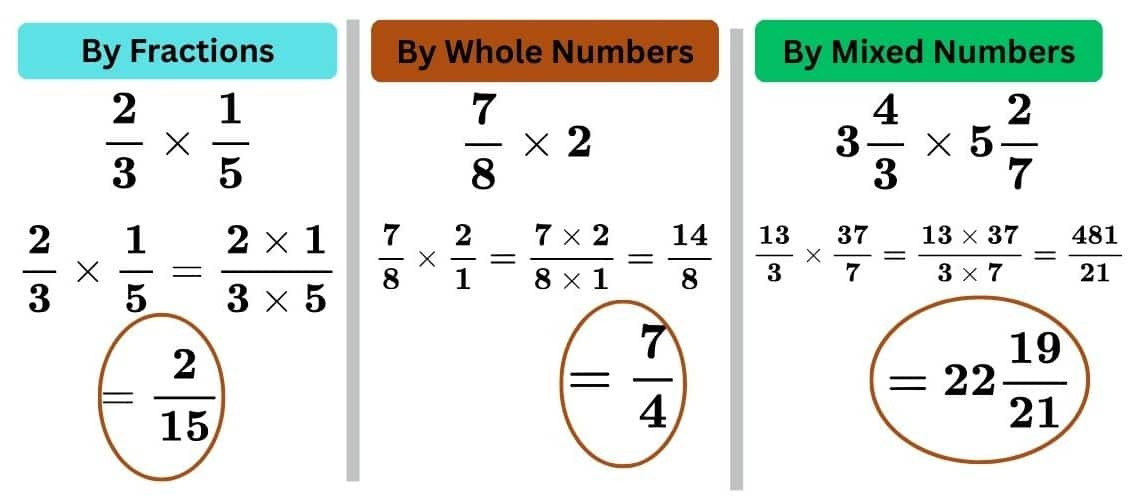
Division of Fractions

Why are Class 7 Maths Chapter 8 Working with Fractions Question Answers Important?
People use fractions in almost every topic, making them a very important part of mathematics. Understanding fractions properly will make other topics like decimals, percentages, and ratios easy. Students also find word problems simpler when they know how to multiply and divide fractions. Class 7 Maths chapter 8 Working With Fractions question answers also become easier when the basics of fractions are clear. Here’s why these question answers are important.
- They help students learn multiplication and division of fractions in a simple way, which is also useful in daily life and other subjects.
- Solving these questions builds confidence in word problems and improves calculation skills.
- In higher classes, such as Class 8 and Class 9, students revisit fractions in algebra and equations, which makes this chapter a precursor to future learning.
- Practising Class 7 Maths Working With Fractions question answers become simpler when students already understand fractions well from this chapter.
NCERT Solutions for Class 7 Mathematics Chapter Wise
For students' preparation, Careers360 has gathered all Class 7 Maths NCERT solutions here for quick and convenient access.
NCERT Books and NCERT Syllabus
Download NCERT books and check the syllabus for Class 7 Maths from the links given below.
Frequently Asked Questions (FAQs)
Fractions are used in daily activities like measuring ingredients, dividing objects equally, calculating discounts, or sharing money or food in equal parts.
No, multiplication of fractions follows the commutative property: a/b × c/d = c/d × a/b
So, the order of multiplication does not affect the result.
The reciprocal of a fraction is obtained by reversing its numerator and denominator.
Example: The Reciprocal of 3/5 is 5/3.
Careers360 provides links for the NCERT Solutions for class 7 Maths for free. Students can find the links in the tail part of this article. These solutions are made by experienced teachers following the latest guidelines.
This chapter covers the following operations of Fractions:
Addition and Subtraction of Fractions
Multiplication of Fractions
Division of Fractions
Here are the steps to convert an improper fraction to a mixed fraction.
Divide the numerator by the denominator.
The quotient is the whole number part.
The remainder divided by the denominator forms the fractional part.
Yes, for Class 7 school exams, Solutions of the NCERT textbook are sufficient. For extra practice purposes, students can use the NCERT Exemplar and various books such as RS Aggarwal, which can also help strengthen the concepts.
No. Division by 0 is undefined for any number, including fractions.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
