RD Sharma Solutions Class 12 Mathematics Chapter 10 VSA

Q: Are the RD Sharma solution books enough for the students to refer to their doubts?

The RD Sharma class 12th exercise VSA books is enough for the students to prepare for the public exams regarding this the 10th chapter in mathematics.

Q: What makes the RD Sharma reference materials special than the other resources?

The questions for the public exams are mostly picked from the practice question section given in the RD Sharma books. Therefore, preparing with these books is ultimately preparing for the public exams which makes it special.

Q: At what minimum cost is the RD Sharma reference books available?

The RD Sharma books are found free of cost at the Career 360 website. Therefore, the students need not pay to buy such authorized reference books

Q: Can the RD Sharma books be used offline?

Even though the RD Sharma class 12th exercise VSA solutions are available online, they can be downloaded to the device for later use.

Q: How many VSA questions for the 10th chapter of mathematics given in the RD Sharma reference book?

There are 30 questions given in the textbook and the RD Sharma reference material contains the answers for all these questions.

RD Sharma Solutions Class 12 Mathematics Chapter 10 VSA

Edited By Satyajeet Kumar | Updated on Jan 20, 2022 06:07 PM IST

RD Sharma Class 12th Exercise VSA is the mostly used solutions material by the class 12 students. This set of books are an asset to any student who is preparing for the public exams. The concepts in mathematics chapter differentiation are well-covered in this book. This chapter consists of 14 exercises, ex 10.1 to 10.14. The VSA or the Very Short Answer part has 30 questions for which the answers can be found at the RD Sharma Class 12th Exercise VSA reference book.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics

This Story also Contains

RD Sharma Class 12 Solutions Chapter 10 VSA Differentiation - Other Exercise
Differentiation Excercise: VSA
RD Sharma Chapter-wise Solutions

Also Read - RD Sharma Solution for Class 9 to 12 Maths

The solutions are provided by various experts in the domain of mathematics, this makes the RD Sharma Class 12th Exercise VSA Solutions book very much reliable. The answers are solved in various methods for the welfare of the students so that, they can rely on the ones that they feel easy.

RD Sharma Class 12 Solutions Chapter 10 VSA Differentiation - Other Exercise

Differentiation Excercise: VSA

Differentiation exercise Very short answers question 1

Answer:
The answer will be $\frac{1}{e}$
Hint:
If $f(x)=\log _{e}\left(\log _{e} x\right)$ then write the value of $f^{\prime}(e)$
Given:
$\frac{d}{d x} \log _{e} x=\frac{1}{x}$
Solution:
$\begin{aligned} &f(x)=\log _{e}\left(\log _{e} x\right) \\\\ &f^{\prime}(x)=\frac{d}{d x}\left[\log _{e}\left(\log _{e} x\right)\right] \end{aligned}$
$=\frac{1}{\log _{e} x} \cdot \frac{d}{d x} \log _{e} x$
$\begin{aligned} &f^{\prime}(x)=\frac{1}{\log _{e} x}\times \frac{1}{x} \\\\ &f^{\prime}(e)=\frac{1}{\log _{e} e}\times \frac{1}{e} \\\\ &f^{\prime}(e)=\frac{1}{e} \end{aligned}$
So, the answer will be $\frac{1}{e}$

Differentiation exercise Very short answers question 2

Answer:
The answer of given question is 1.
Hint:
$(f o f)(x)=f[f(x)]$
Given:
$\text { If } f(x)=x+1 \text { then find } \frac{d}{d x}(\text { fof })(x)$
Solution:
$\begin{aligned} &f(x)=x+1 \\\\ &f[f(x)]=f(x+1) \\\\ &=x+1+1 \end{aligned}$
$\begin{aligned} &\frac{d}{d x}(f o f)(x)=\frac{d}{d x}(x+2) \\\\ &=1 \end{aligned}$
so, the answer will be 1

Differentiation exercise Very short answers question 3

Answer:
The answer of the following will be $\frac{2}{e}$
Given:
$\text { If}f^{\prime}(1)=2 \text { and } y=f\left(\log _{e} x\right), \text { find } \frac{d y}{d x} \text { at } x=e$
Hint:
$\frac{d y}{d x}=\frac{d}{d x}\left[f\left(\log _{e} x\right)\right]$
Solution:
$\begin{aligned} &y=f\left(\log _{e} x\right) \\\\ &\Rightarrow \frac{d y}{d x}=f^{\prime}\left(\log _{e} x\right) \cdot \frac{d}{d x}\left(\log _{e} x\right) \\\\ &\Rightarrow \frac{d y}{d x}=\frac{f^{\prime}\left(\log _{e} x\right)}{x} \end{aligned}$
$\begin{aligned} &\Rightarrow \frac{d y}{d x}(\text { at } x=e)=\frac{f^{\prime}\left(\log _{e} e\right)}{e} \\\\ &=\frac{f^{{}'}1}{e} \text { since } f^{{}'} 1=2 \\\\ &=\frac{2}{e} \end{aligned}$
∴So, the answer will be $\frac{2}{e}$

Differentiation exercise Very short answers question 4

Answer:
The answer of the given question will be $\frac{1}{2}$ .
Given:
If $f(1)=4 \text { and } f^{\prime}(1)=2$ , find the value of derivative $\log \left[f\left(e^{x}\right)\right]$ with respect to $x$ at the point $x=0$
Hint:
$\frac{d}{d x}(\log x)=\frac{1}{x} \& \frac{d}{d x}\left(e^{x}\right)=e^{x} \& \frac{d}{d x}[f(x)]=f^{\prime}(x)$
Solution:
$\begin{aligned} &\frac{d u}{d x}=\frac{d}{d x} \log \left[f\left(e^{x}\right)\right] \\\\ &=\frac{1}{f\left(e^{x}\right)} \cdot \frac{d}{d x}\left[f\left(e^{x}\right)\right] \end{aligned}$
$\begin{aligned} &=\frac{1}{f\left(e^{x}\right)} \cdot f^{\prime}\left(e^{x}\right) \cdot \frac{d}{d x}\left(e^{x}\right) \\\\ &\Rightarrow \frac{d u}{d x}=\frac{f^{\prime}\left(e^{x}\right) \cdot e^{x}}{f\left(e^{x}\right)} \end{aligned}$
$\begin{aligned} &\Rightarrow \frac{d u}{d x}(\text { at } x=0)=\frac{f^{\prime}\left(e^{0}\right) \cdot e^{0}}{f\left(e^{0}\right)} \\\\ &=\frac{f^{\prime}(1) \cdot 1}{f(1)} \end{aligned}$
$\begin{aligned} &=\frac{2}{4} \\\\ &=\frac{1}{2} \end{aligned}$
∴So, the answer will be $\frac{1}{2}$

Differentiation exercise Very short answers question 5

Answer:
The answer of the given question will be 2.
Given:
$\text { If } f^{\prime}(x)=\sqrt{2 x^{2}-1} \text { and } y=f\left(x^{2}\right) \text { then find } \frac{d y}{d x} \text { at } x=1$
Hint:
$\frac{d y}{d x}=\frac{d}{d x}\left[f\left(x^{2}\right)\right]=f^{\prime}\left(x^{2}\right) \cdot \frac{d}{d x}\left(x^{2}\right)$
Solution:
$\begin{aligned} &y=f\left(x^{2}\right) \\\\ &\Rightarrow \frac{d y}{d x}=f^{\prime}\left(x^{2}\right) \cdot \frac{d}{d x}\left(x^{2}\right) \\\\ &=2 x \cdot f^{\prime}\left(x^{2}\right) \end{aligned}$
$\begin{aligned} &\Rightarrow \frac{d y}{d x}=2 x \cdot \sqrt{2\left(x^{2}\right)^{2}-1} \\\\ &\Rightarrow \frac{d y}{d x}=2 x \cdot \sqrt{2 x^{4}-1} \\\\ &\Rightarrow \frac{d y}{d x}(\text { at } x=1)=2.1 \cdot \sqrt{2(1)^{4}-1} \end{aligned}$
$\begin{aligned} &=2 \sqrt{2-1} \\\\ &=2 \times 1 \\\\ &=2 \end{aligned}$
So, the answer will be 2.

Differentiation exercise Very short answers question 7

Answer:
The answer of the given question will be 1.
Given:
If $\sin ^{-1}(\sin x),-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}$ then write the value of $\frac{d y}{d x} \text { for } x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
Hint:
$x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
Solution:
$\begin{aligned} &\sin ^{-1}(\sin x)=x, x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right] \\\\ &\Rightarrow \frac{d y}{d x}=\frac{d}{d x}(x)=1 \\\\ &\therefore \frac{d y}{d x}=1 \end{aligned}$
So the answer will be 1.

Differentiation exercise Very short answers question 8

Answer:
The answer of the given question will be -1.
Given:
$\text { If } \frac{\pi}{2} \leq x \leq \frac{3 \pi}{2} \text { and } y=\sin ^{-1}(\sin x) \text { find } \frac{d y}{d x}$
Hint:
Here, $\frac{\pi}{2} \leq x \leq \frac{3 \pi}{2}$
Solution:
$\begin{aligned} &y=\sin ^{-1}(\sin x)=(\pi-x) \\\\ &\frac{d y}{d x}=\frac{d}{d x}(\pi-x)=-1 \end{aligned}$
So the answer of $\frac{d y}{d x}=-1$

Differentiation exercise Very short answers question 9

Answer:
The answer of the given question will be -1.
Given:
$\text { If } \pi \leq x \leq 2 \pi \text { and } y=\cos ^{-1}(\cos x) \text { find } \frac{d y}{d x}$
Hint:
$\pi \leq x \leq 2 \pi$
Solution:
$\begin{aligned} &y=\cos ^{-1}(\cos x)=(2 \pi-x) \\\\ &\frac{d y}{d x}=\frac{d}{d x}(2 \pi-x) \\\\ &=-1 \end{aligned}$
So the answer of $\frac{d y}{d x}=-1$

Differentiation exercise Very short answers question 10

Answer:
The answer of the given question is $\frac{2}{1+x^{2}}$
Given:
$\text { Ify }=\sin ^{-1}\left[\frac{2 x}{1+x^{2}}\right] \text { write the value of } \frac{d y}{d x} \text { for } x>1 \text { . }$
Hint:
$\text { putting } x=\tan \theta$
Solution:
$\begin{aligned} &y=\sin ^{-1}\left[\frac{2 x}{1+x^{2}}\right] \\\\ &y=\sin ^{-1}\left[\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right] \end{aligned}$
$\begin{aligned} &y=\sin ^{-1} \sin 2 \theta \\\\ &y=2 \theta \\\\ &\Rightarrow y=2 \tan ^{-1} x \end{aligned}$
$\begin{aligned} &\Rightarrow \frac{d y}{d x}=2 \cdot \frac{1}{1+x^{2}} \\\\ &\Rightarrow \frac{d y}{d x}=\frac{2}{1+x^{2}} \end{aligned}$
So the answer will be $\frac{2}{1+x^{2}}$

Differentiation exercise Very short answers question 11

Answer:
The answer of the given question will be 2
Given:
$\text { Iff }(0)=f(1)=0, f^{\prime}(1)=2 \text { and } y=f\left(e^{x}\right) e^{f(x)}$ write the value of $\frac{d y}{d x} \text { for } x=0$
Hint:
$\frac{d}{d x} u v=u \cdot \frac{d}{d x} \cdot v+. v \frac{d}{d x} u$
Solution:
$\frac{d y}{d x}=\left[f\left(e^{x}\right) e^{f(x)}\right]=\frac{d}{d x}\left[f\left(e^{x}\right) \cdot e^{f(x)}+f\left(e^{x}\right) \cdot \frac{d}{d x} e^{f(x)}\right]$
$=\frac{d}{d x} f^{\prime}\left(e^{x}\right) \cdot \frac{d}{d x} e^{x} \cdot e^{f(x)}+f\left(e^{x}\right) \cdot e^{f(x)} \cdot \frac{d}{d x}[f(x)]$
$\begin{aligned} &\Rightarrow \frac{d y}{d x}=f^{\prime}\left(e^{x}\right) \cdot e^{x} \cdot e^{f(x)}+f\left(e^{x}\right) \cdot e^{f(x)} \cdot f^{\prime}(x) \\\\ &\Rightarrow \frac{d y}{d x}=f^{\prime}\left(e^{0}\right) \cdot e^{0} \cdot e^{f(0)}+f\left(e^{0}\right) \cdot e^{f(0)} \cdot f^{\prime}(0) \end{aligned}$
$\begin{aligned} &=f^{\prime}(1) \cdot 1 \cdot e^{f(0)}+f(1) \cdot e^{f(0)} \cdot f^{\prime}(0) \\\\ &=2 . e^{0}+0 . e^{0} \cdot 2 \\\\ &=2.1+0 \\\\ &=2 \end{aligned}$
So the answer of $\frac{d y}{d x}=2$

Differentiation exercise Very short answers question 12

Answer:
The answer of the given question will be -2x.
Given:
$\text { If } y=x|x| \text { find } \frac{d y}{d x} \text { for } x<0$
Hint:
$|x|=\left\{\begin{array}{cc} x, & x \geq 0 \\ -x, & x<0 \end{array}\right\}$
Solution:
$\begin{aligned} &y=x|x| \\\\ &y=x(-x,) \text { since } x<0 \\\\ &=-x^{2} \end{aligned}$
$\begin{aligned} &\frac{d y}{d x}=-\frac{d}{d x}\left(x^{2}\right)=-2 x \\\\ &\text { So, the } \frac{d y}{d x}=-2 x \end{aligned}$

Differentiation exercise Very short answers question 13

Answer:
The answer of the given question will be 0.
Given:
$\text { If } y=\sin ^{-1} x+\cos ^{-1} x \text { find } \frac{d y}{d x}$
Hint:
$\begin{aligned} &\frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^{2}}} \\\\ &\frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^{2}}} \end{aligned}$
Solution:
$\begin{aligned} &y=\sin ^{-1} x+\cos ^{-1} x \\\\ &\Rightarrow \frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}-\frac{1}{\sqrt{1-x^{2}}} \\\\ &=0 \end{aligned}$
So, the answer of $\frac{d y}{d x}=0$

Differentiation exercise Very short answers question 14

Answer:
$\text { The value of } \frac{d y}{d x}=-\tan \theta / 2$
Given:
$\text { If } x=a(\theta+\sin \theta), y=a(1+\cos \theta) \text { find } \frac{d y}{d x}$
Hint:
$\begin{aligned} &\frac{d}{d x}(\sin x)=\cos x \\\\ &\frac{d}{d x}(\cos x)=-\sin x \end{aligned}$
Solution:
$\begin{aligned} &\frac{d x}{d \theta}=a \frac{d}{d \theta}(\theta+\sin \theta) \\\\ &=a[1+\cos \theta] \end{aligned}$
$\begin{aligned} &\frac{d y}{d \theta}=a \frac{d}{d \theta}[1+\cos \theta] \\\\ &=-a \sin \theta \end{aligned}$
$\begin{aligned} &\frac{d y}{d x}=\frac{-a \sin \theta}{a(1+\cos \theta)} \\\\ &=\frac{-\sin \theta}{1+\cos \theta} \end{aligned}$
$=\frac{-2 \sin ^{\theta} / 2 \cos ^{\theta} / 2}{2 \cos ^{2} \theta / 2}$ using formula of half angle
$=-\tan \theta / 2$
So, the answer of $\frac{d y}{d x}=-\tan \theta / 2$

Differentiation exercise Very short answers question 15

Answer:
$-1$
Hint:
$\begin{aligned} &\text { Using (1) } 1-\cos 2 x=2 \sin ^{2} x\\ &\text { (2) } 1+\cos 2 x=2 \cos ^{2} x \end{aligned}$
Given:
$y=\tan ^{-1}\left(\sqrt{\frac{1-\cos 2 x}{1+\cos 2 x}}\right)$
Solution:
$\begin{aligned} &y=\tan ^{-1}\left(\sqrt{\frac{1-\cos 2 x}{1+\cos 2 x}}\right) \\\\ &y=\tan ^{-1}\left(\sqrt{\frac{2 \sin ^{2} x}{2 \cos ^{2} x}}\right) \end{aligned}$
Using
$\begin{aligned} &1-\cos 2 x=2 \sin ^{2} x \\\\ &1+\cos 2 x=2 \cos ^{2} x \\\\ &y=\tan ^{-1}\left(\sqrt{\tan ^{2} x}\right) \end{aligned}$
$\begin{aligned} &y=\tan ^{-1}(-\tan x)\left[-\frac{\pi}{2}<x<0\right] \\\\ &y=-x \quad\left[\because \tan ^{-1}(\tan x)=x\right] \end{aligned}$
Differentiate it w.r.t x, we get
$\begin{aligned} &\frac{d y}{d x}=\frac{d(-x)}{d x} \\\\ &\frac{d y}{d x}=-1 \text { for } x \in\left(-\frac{\pi}{2}, 0\right) \end{aligned}$

Differentiation exercise Very short answers question 16

Answer:
The value of $\frac{d y}{d x} \text { at } x=e \text { is } 2 e^{e}$
Hint:
Taking logarithm on both sides.
Given:
$y=x^{x}$
Solution:
$y=x^{x}$
Taking logarithm on both sides.
$\log y=x \log x$
Differentiating with respect to x on both sides.,
$\frac{1}{y} \frac{d y}{d x}=x \cdot \frac{1}{x}+1 . \log x$
$\begin{aligned} &=1+\log x \\\\ &\Rightarrow \frac{d y}{d x}=y(1+\log x) \\\\ &\Rightarrow x^{x}(1+\log x) \end{aligned}$
So at $x=e$ ,
$\begin{aligned} &\frac{d y}{d x}=e^{e}(1+\log e) \\\\ &=e^{e}(1+1) \\\\ &=2 e^{e} \end{aligned}$

Differentiation exercise Very short answers question 17

Answer:
The value of
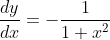$\frac{d y}{d x}=-\frac{1}{1+x^{2}}$ Hint:
Using the chain rule of differentiation.
Given:
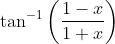$\tan ^{-1}\left(\frac{1-x}{1+x}\right)$ Solution:
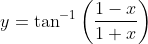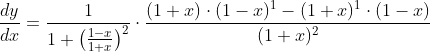
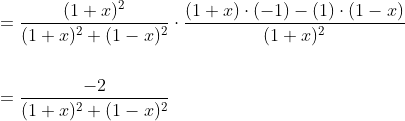
$y=\tan ^{-1}\left(\frac{1-x}{1+x}\right)$ Using the chain rule of differentiation $\frac{d y}{d x}=\frac{1}{1+\left(\frac{1-x}{1+x}\right)^{2}} \cdot \frac{(1+x) \cdot(1-x)^{1}-(1+x)^{1} \cdot(1-x)}{(1+x)^{2}}$ $\begin{aligned} &=\frac{(1+x)^{2}}{(1+x)^{2}+(1-x)^{2}} \cdot \frac{(1+x) \cdot(-1)-(1) \cdot(1-x)}{(1+x)^{2}} \\\\ &=\frac{-2}{(1+x)^{2}+(1-x)^{2}} \end{aligned}$

$\frac{d y}{d x}=-\frac{1}{1+x^{2}}$

Differentiation exercise Very short answers question 18

Answer:
The value of $\frac{d y}{d x} \text { is } \frac{1}{x \log _{e} a}$
Hint:
By using the properties of logarithm.
Given:
$y=\log _{a} x$
Solution:
$y=\log _{a} x$
$=\frac{\log _{e} x}{\log _{e} a}$
$\frac{d y}{d x}=\frac{1}{\log _{e} a} \cdot \frac{1}{x}$
$=\frac{1}{\operatorname{xlog}_{e} a}$

Differentiation exercise Very short answers question 19

Answer:
$\cos \operatorname{ec} 2 x$
Hint:
By using the chain rule of differentiation
Given:
$y=\log \sqrt{\tan x}$
Solution:
$\text { i. } e \cdot \frac{d y}{d x}=\frac{d(\log \sqrt{\tan x})}{d(\sqrt{\tan x})} \cdot \frac{d(\sqrt{\tan x})}{d(\tan x)} \cdot \frac{d(\tan x)}{d x}$
$\begin{aligned} &=\frac{1}{\sqrt{\tan x}} \cdot \frac{1}{2 \sqrt{\tan x}} \cdot \sec ^{2} x \\\\ &=\frac{\sec ^{2} x}{2 \tan x} \\\\ &=\frac{1+\tan ^{2} x}{2 \tan x} \end{aligned}$
$\begin{aligned} &=\frac{1}{2}(\tan x+\cot x) \\\\ &=\frac{1}{2}\left[\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\right] \end{aligned}$
$=\frac{1}{2}\left[\frac{\sin ^{2} x+\cos ^{2} x}{\sin x \cos x}\right] \quad\left[\because \sin ^{2} x+\cos ^{2} x=1\right]$
$=\frac{1}{2} \times \frac{2}{\sin 2 x}=\cos e c 2 x \quad[\sin 2 x=2 \sin x \cos x]$

Differentiation exercise Very short answers question 20

Answer:
$\frac{d y}{d x}=0, \text { for all } x \in R$
Hint:
$-1<\frac{1-x^{2}}{1+x^{2}} \leq 1 \text { holds for all } x \in R$
Given:
$y=\sin ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)+\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)$
Solution:
$-1<\frac{1-x^{2}}{1+x^{2}} \leq 1 \text { holds for all } x \in R$
So,
$y=\sin ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)+\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right)=\frac{\pi}{2} ; \text { for all } x \in R$
$\therefore \sin ^{-1} m+\cos ^{-1} m=\frac{\pi}{2}, m \in(-1,1)$
Hence,
$\frac{d y}{d x}=0, \text { for all } x \in R$

Differentiation exercise Very short answers question 21

Answer:
$\frac{d y}{d x}=\{0, x \geq 0\} \text { does not exist for } x<0$
Hint:
changing $\sec ^{-1}\left(\frac{x+1}{x-1}\right) \text { into } \cos ^{-1}\left(\frac{x-1}{x+1}\right)$
Given:
$y=\sec ^{-1}\left(\frac{x+1}{x-1}\right)+\sin ^{-1}\left(\frac{x+1}{x-1}\right)$
Solution:
$\begin{aligned} &y=\sec ^{-1}\left(\frac{x+1}{x-1}\right)+\sin ^{-1}\left(\frac{x+1}{x-1}\right) \\\\ &y=\cos ^{-1}\left(\frac{x-1}{x+1}\right)+\sin ^{-1}\left(\frac{x+1}{x-1}\right) \end{aligned}$
Which exists for
$-1 \leq\left(\frac{x-1}{x+1}\right) \leq 1\text { and is equal to } \frac{\pi}{2}$
Now,
$\frac{x-1}{x+1} \leq 1$
$\begin{aligned} &\Rightarrow \frac{x-1}{x+1}-1 \leq 0 \\\\ &\Rightarrow \frac{x-1}{x+1}-\frac{x+1}{x+1} \leq 0 \\\\ &\Rightarrow-\frac{2}{x+1} \leq 0 \end{aligned}$
$\begin{aligned} &\Rightarrow x+1>0 \\\\ &\Rightarrow x>1 \ldots \ldots \ldots . . \text { (i) } \end{aligned}$
Also,
$\begin{aligned} &\frac{x-1}{x+1} \geq-1 \\\\ &\Rightarrow \frac{x-1}{x+1}+1 \geq 0 \end{aligned}$
$\begin{aligned} &\Rightarrow \frac{x-1}{x+1}+\frac{x+1}{x+1} \geq 0\\\\ &\Rightarrow \frac{2 x}{x+1} \geq 0\\\\ &\Rightarrow x \geq 0 \text { or } x<-1 \ldots \ldots \ldots \ldots \ldots \ldots(ii) \end{aligned}$
Comparing equations (i) and (ii) we understand that the condition satisfying both inequalities is $x\geq 0$ . So, for $x\geq 0$
$y=\cos ^{-1}\left(\frac{x-1}{x+1}\right)+\sin ^{-1}\left(\frac{x+1}{x-1}\right)=\frac{\pi}{2}$ , which is a constant
So,
$\frac{d y}{d x}=\{0, x \geq 0\} \text { does not exist for } x<0$

Differentiation exercise Very short answers question 22

Answer: The value of $\frac{d y}{d x}=\frac{1}{(1-x)^{2}}$
Hint:
we replace $1+x+x^{2}+\cdots \infty \text { by } \frac{1}{1-x}$
Given:
$|x|<1 \text { and } y=1+x+x^{2}+\cdots \infty$
Solution:
Since $|x|<1$ ,
$\begin{aligned} &y=1+x+x^{2}+\cdots \infty \\\\ &=\frac{1}{1-x} \\\\ &\therefore \frac{d y}{d x}=-\frac{1}{(1-x)^{2}} \cdot-1 \end{aligned}$
$\frac{d y}{d x}=\frac{1}{(1-x)^{2}}$

Differentiation exercise Very short answers question 23

Answer:
1
Hint:
Using $\frac{d u}{d v}=\frac{\frac{d u}{d x}}{\frac{d v}{d x}}$
Given:
$\begin{aligned} &u=\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) \text { and } v=\tan ^{-1}\left(\frac{2 x}{1+x^{2}}\right) \\ &\text { where }-1<x<1 \end{aligned}$
Solution:
$u=\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)$ ..............(i)
Put $x=\tan \theta$
$u=\sin ^{-1}\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)$
$u=\sin ^{-1}(\sin 2 \theta) \quad\left[\because \frac{2 \tan \theta}{1+\tan ^{2} \theta}=\sin 2 \theta\right]$
$u=2 \theta \quad\left[\sin ^{-1}(\sin \theta)=\theta\right]$
$u=2 \tan ^{-1} x \quad\left[\because \theta=\tan ^{-1} x\right]$
Differentiating it w.r.t x we get
$\frac{d u}{d x}=\frac{2}{1+x^{2}}$
Again we have,
$\begin{aligned} &v=\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right) \\\\ &\text { Put } x=\tan \theta \\\\ &v=\tan ^{-1}\left(\frac{2 \tan \theta}{1-\tan ^{2} \theta}\right) \end{aligned}$
$v=\tan ^{-1}(\tan 2 \theta) \quad\left[\because \tan 2 \theta=\frac{2 \tan \theta}{1-\tan ^{2} \theta}\right]$
$v=2 \theta \quad\left[\because \tan ^{-1}(\tan \theta)=\theta\right]$
$v=2 \tan ^{-1} x \quad\left[\because \theta=\tan ^{-1} x\right]$
Differentiating it w.r.t x, we get
$\frac{d v}{d x}=\frac{2}{1+x^{2}}$
now,
$\begin{aligned} &\frac{d u}{d v}=\frac{\frac{d u}{d x}}{\frac{d v}{d x}}=\frac{\frac{2}{\left(1+x^{2}\right)}}{\frac{2}{\left(1+x^{2}\right)}} \\\\ &\frac{d u}{d v}=1 \end{aligned}$

Differentiation exercise Very short answers question 24

Answer:
The value of $f^{\prime}(1) \text { is } 0$
Hint:
Using the chain rule of differentiation.
Given:
$f(x)=\log \left\{\frac{u(x)}{v(x)}\right\}, u(1)=v(1) \text { and } u^{\prime}(1)=v^{\prime}(1)=2$
Solution:
Using the chain rule of differentiation
$f^{\prime}(x)=\frac{1}{\frac{u(x)}{v(x)}} \cdot \frac{v(x) \cdot u^{\prime}(x)-v^{\prime}(x) \cdot u(x)}{(v(x))^{2}}$
$f^{\prime}(x)=\frac{v(x) \cdot u^{\prime}(x)-v^{\prime}(x) \cdot u(x)}{u(x) \cdot v(x)}$
Putting $x=1$
$f^{\prime}(1)=\frac{v(1) \cdot u^{\prime}(1)-v^{\prime}(1) \cdot u(1)}{u(1) \cdot v(1)}$
$=\frac{2 v(1) \cdot-2 u(1)}{u(1) \cdot v(1)}$
Since,
$\begin{aligned} &u(1)=v(1) \\\\ &2 v(1) \cdot-2 v(1)=0 \\\\ &\text { i.e, } f^{\prime}(1)=0 \end{aligned}$

Differentiation exercise Very short answers question 25

Answer:
The value of $\frac{d y}{d x}=\frac{1}{x}, x \neq 0$
Hint:
By using the properties of logarithm.
Given:
$y=\log |3 x|, x \neq 0$
Solution:
$y=\log |3 x|$
So,
$\begin{aligned} &\frac{d y}{d x}=\frac{1}{3 x} \cdot 3 \\\\ &=\frac{1}{x}, x \neq 0 \\\\ &\frac{d y}{d x}=\frac{1}{x}, x \neq 0 \end{aligned}$

Differentiation exercise Very short answers question 26

Answer:
$f^{\prime}(x)$ is an odd function.
Hint:
Differentiate equation on the both sides with respect to x.
Given:
$f^{}(x)$ is an even function.
Solution:
$f^{}(x)$ is an even function.
This means that $f(-x)=f(x)$
If we differentiate this equation on both sides with respect to x, we get.
$\begin{aligned} &f^{\prime}(x) \cdot(-1)=f^{\prime}(x) \\\\ &\text { or },-f^{\prime}(-x)=f^{\prime}(x) \end{aligned}$
i.e. $f^{\prime}(x)$ is an odd function.

Differentiation exercise Very short answers question 27

Answer:
$f^{\prime}(x)$ is an even function
Hint:
Differentiate equation on the both sides with respect to x.
Given:
$f(x)$ is an odd function.
Solution:
$f(x)$ is an odd function.
This means that $f(-x)=-f(x)$
If we differentiate this equation on both sides with respect to x, we get.
$\begin{aligned} &f^{\prime}(-x) \cdot(-1)=-f^{\prime}(x) \\\\ &\text { or, } f^{\prime}(-x)=f^{\prime}(x) \end{aligned}$
i.e, $f^{\prime}(x)$ is an even function

Differentiation exercise Very short answers question 28

Answer:
Derivation of $sin \; x$ with respect to $cos \; x$ is $-cot \; x.$
Hint:
By using the chain rule of differentiation.
Given:
Derivation of $sin \; x$ with respect to $cos \; x$ is $\cos \; x.$
Solution:
We have to find
$\frac{d}{d(\cos x)}(\sin x)$
So, we use the chain rule of differentiation to evaluate this.
$\frac{d}{d(\cos x)}(\sin x)=\frac{d(\sin x)}{d x} \cdot \frac{d x}{d(\cos x)}$
$\begin{aligned} &=\cos x \cdot \frac{1}{-\sin x} \\\\ &=-\cot x \end{aligned}$

Differentiation exercise Very short answers question 29

Answer:
The value of $\frac{d y}{d x} \text { is }-e^{x} \tan e^{x}$
Hint:
Differentiating both sides with respect to x.
Given:
$y=\log \cos e^{x}$
Solution:
$y=\log \cos e^{x}$
Differentiating both sides with respect to x.
$\frac{d y}{d x}=\frac{d\left\{\log \left(\cos e^{x}\right)\right\}}{d x}$
$\frac{d y}{d x}=\frac{1}{\cos e^{x}} \cdot \frac{d\left(\cos e^{x}\right)}{d e^{x}} \cdot \frac{d e^{x}}{d x}\left(\therefore \frac{d \log x}{d x}=\frac{1}{x}\right)$
$=\frac{1}{\cos e^{x}} \cdot\left(-\sin e^{x}\right) \cdot e^{x}\left(\therefore \frac{d e^{x}}{d x}=e^{x}\right)$
$\begin{aligned} &=\frac{-\sin e^{x}}{\cos e^{x}} \cdot e^{x} \\\\ &=-\tan e^{x} \cdot e^{x} \\\\ &=-e^{x} \cdot \tan e^{x} \end{aligned}$

This part consists of concepts that are present in every exercise of the chapter 10. Topics like differentiation of a function, inverse trigonometric functions, differentiation of infinite series, differentiation of parametric functions and many more are included in this section. Even though there is too much to learn, the RD Sharma Class 12 VSA material will require only less efforts from the students’ side.

Advantages that a student can gain while utilising the RD Sharma class 12 solutions:

Accurate answers:

The students need not worry regarding the accuracy of the solutions given in the RD Sharma class 12th exercise VSA books. All the answers are provided by a group of experts and professionals. Therefore, the steps in the RD Sharma class 12 Solutions Differentiation VSA are clearly explained in a way that the students can grasp easily.

Studying the concepts in advance:

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Not every concept in mathematics for the class 12 students requires to be taught be the teacher, there are easy topics that the students can learn on their own. This gives them the confidence to face such questions in the examination. These sums can be learnt before-hand using the Class 12 RD Sharma chapter 10 exercise VSA.

Practice sums:

Apart from the solved sums given for each question present in the book, the RD Sharma class 12th exercise VSA also contains extra sums for the students to test their understanding capability.

Multiple methods of solving a sum:

In mathematics, there are may methods in which a sum can be solved. The RD Sharma class 12th exercise VSA gives the exposure to the students of these various methods.

Improvement in scores:

Once the students use the RD Sharma books to practice the sums every day, they can gradually see the growth of their performance. Even the previous batch students have given positive feedback about this set of books.

Costless:

Who would not wish to have something for free of cost? The entire RD Sharma set of books can be found at the Career 360 website for free of cost. This is another strong reason why a student must make use of this wonderful opportunity.

RD Sharma Chapter-wise Solutions

Frequently Asked Questions (FAQs)

1. Are the RD Sharma solution books enough for the students to refer to their doubts?

The RD Sharma class 12th exercise VSA books is enough for the students to prepare for the public exams regarding this the 10th chapter in mathematics.

2. What makes the RD Sharma reference materials special than the other resources?

The questions for the public exams are mostly picked from the practice question section given in the RD Sharma books. Therefore, preparing with these books is ultimately preparing for the public exams which makes it special.

3. At what minimum cost is the RD Sharma reference books available?

The RD Sharma books are found free of cost at the Career 360 website. Therefore, the students need not pay to buy such authorized reference books

4. Can the RD Sharma books be used offline?

Even though the RD Sharma class 12th exercise VSA solutions are available online, they can be downloaded to the device for later use.

5. How many VSA questions for the 10th chapter of mathematics given in the RD Sharma reference book?

There are 30 questions given in the textbook and the RD Sharma reference material contains the answers for all these questions.