NCERT Solutions for Class 8 Maths Chapter 9 Mensuration
In the realm of mathematics, mensuration governs shapes, ensuring every inch is accounted for. Children often wonder about the geometry around them—"What shape is my book?", "How were the pyramids measured?", or even "How much wax is needed to make a candle for my school project?" and "What shape is a Christmas tree?" All these curious questions relate directly to the concept of Mensuration. They will clearly understand these shapes in detail after completing the Mensuration chapter, which is Class 8 Maths NCERT Chapter 9. In this section of Mathematics, we discuss the length, volume, and surface areas of various types of quadrilaterals. These NCERT solutions for Class 8 on Mensuration are designed to guide students step-by-step whenever they feel confused while solving exercise problems.
This Story also Contains
- Mensuration Class 8 Questions And Answers PDF Free Download
- NCERT Solutions for Class 8 Maths Chapter 9: Exercise Questions
- Mensuration Class 8 Chapter 9: Topics
- Mensuration Class 8 Solutions - Important Formulae
- NCERT Solutions for Class 8 Maths: Chapter Wise
Mensuration turns geometry into a tool, letting us calculate the space we occupy in this vast universe. Solving the NCERT Solutions for Class 8 Maths of Chapter 9 will help us excel in board exams and lay a smooth path to learning about these concepts in higher classes. Other competitive exams frequently include many questions from this chapter. These class 8 Mensuration solutions contain many images and diagrams clearly illustrating the shapes because visualisation is often considered the best way to learn. Experienced Careers 360 experts have made these solutions following the latest CBSE guidelines. Download your syllabus, revision notes, and all chapter PDFs here: NCERT.
Mensuration Class 8 Questions And Answers PDF Free Download
Students who wish to access the NCERT solutions for class 8, chapter 9, Mensuration, can click on the link below to download the entire solution in PDF.
NCERT Solutions for Class 8 Maths Chapter 9: Exercise Questions
| Class 8 maths chapter 9 NCERT solutions: Exercise 9.1 Total Questions: 11 Page number: 105-106 |
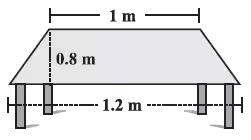
Answer:
Area of the table
= $\frac12$ × sum of parallel sides × distance between parallel sides
= $\frac12$ × (1+1.2) × 0.8
= 0.4×2.2
= 0.88 m2
Answer:
Let the length of the other parallel side be x
area of a trapezium, $\frac12$ ×(10+x)×4=34
⇒ (10+x)=17
⇒ x = 17−10
⇒ x = 7 cm
Hence, the length of the other parallel side is 7 cm.
![]()
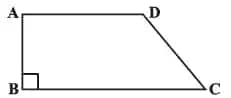
Answer:
BC=48 m, CD=17 m and AD=40 m ,
Length of the fence of a trapezium-shaped field ABCD
= 120m = AB+BC+CD+DA
⇒ 120 = AB+48+17+40
⇒ AB = 15 m
Area of the trapezium
= $\frac12$ × sum of parallel sides × height
= $\frac12$×(40+48)×15
= $\frac12$×(88)×15
= (44)×15
= 660 m2
![]()
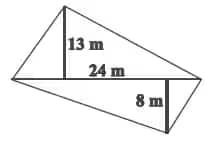
Answer:
The diagonal of a quadrilateral-shaped field is 24 m.
The perpendiculars are 8 m and 13 m.
The area of the field
= $\frac12$ ×d×(h1+h2)
= $\frac12$ ×24×(13+8)
= 12×21
= 252 m2
Question 5: The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Answer:
Area of the rhombus
= $\frac12$ × product of diagonals
= $\frac12$×7.5×12
= 7.5×6
= 45 cm2
Answer:
A rhombus is a type of parallelogram, and the area of the parallelogram is the product of base and height.
So, Area of rhombus = base × height = 5×4.8 = 24
Let the other diagonal be x.
Area of the rhombus = $\frac12$ × product of diagonals
⇒ 24 = 12×8×x
⇒ x = 6 cm
Answer:
Area of 1 tile
= $\frac12$ × product of diagonals
= $\frac12$ ×45×30
= 675 cm2
Area of 3000 tiles
= 675 ×3000
= 202.5 m2
Total cost of polishing
= 202.5 × 4
= Rs. 810

![]()
Answer:
Let the length of the side along the road be x m.
Then, according to the question, the length of the side along the river will be 2x m.
Area of trapezium = $\frac12$h(a+b)
So the equation becomes:
$\frac12\times$100(x+2x)=10500
⇒ 3x = 210
⇒ x = 70
So the length of the side along the river is 2x = 140m.
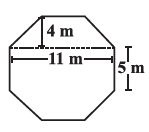
Answer:
Area of octagonal surface = Area of rectangular surface + 2(Area of trapezium surface)
Area of rectangular surface = 11×5 = 55 m2
Area of trapezium surface =
$\frac12$ × 4 (11+5) = 2 × 16 = 32 m2
So, the total area of the octagonal surface = 55 + 2(32) = 55 + 64 = 119 m2
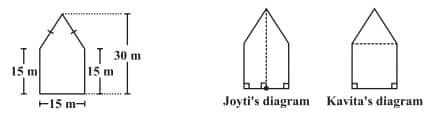
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Answer:
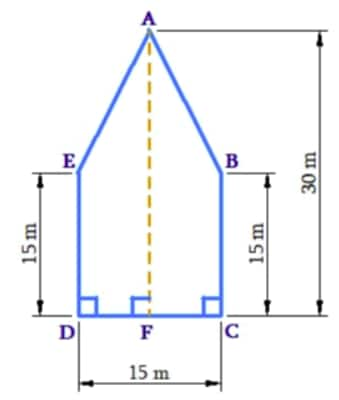
Area of pentagon $\mathrm{ABCDE}=$ Area of trapezium $\mathrm{ABCF}+$ Area of trapezium AEDF
$
\begin{aligned}
& =\frac12 \times(A F+B C) \times F C+\frac12 \times(A F+E D) \times D F \\
& =\frac12 \times(30 \mathrm{~m}+15 \mathrm{~m}) \times \frac{15}2 \mathrm{~m}+\frac12 \times(30+15 \mathrm{~m}) \times \frac{15}2 \mathrm{~m} \\
& =2 \times \frac12(30 \mathrm{~m}+15 \mathrm{~m}) \times \frac{15}2 \\
& =45 \mathrm{~m} \times 7.5 \mathrm{~m} \\
& =337.5 \mathrm{~m}^2
\end{aligned}
$
Thus, the area of the pentagon-shaped park according to Jyoti's way is $337.5 \mathrm{~m}^2$
$
\begin{aligned}
& \text { Area of pentagon } A B C D E=\text { Area of triangle } A B E+\text { Area of square } E B C D \\
& =\frac12 \times B E \times(A F-O F)+F C \times B C[\text { Since, } A O=A F-O F] \\
& =\frac12 \times 15 \times(30-15)+(15 \times 15) \\
& =(\frac12 \times 15 \times 15) \mathrm{m}^2+225 \mathrm{~m}^2 \\
& =112.5 \mathrm{~m}^2+225 \mathrm{~m}^2 \\
& =337.5 \mathrm{~m}^2
\end{aligned}
$
Thus, the area of the pentagon-shaped park according to Kavitha's way is $337.5 \mathrm{~m}^2$
![]()
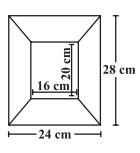
Answer:
The area of the opposite sections will be the same.
So the area of horizontal sections,
= $\frac12$×4(16+24)
= 2(40)
= 80 cm2
And the area of vertical sections,
= $\frac12$×4(20+28)
= 2(48)
= 96 cm2
| Class 8 maths chapter 9 NCERT solutions: Exercise 9.2 Total Questions: 10 Page number: 114 |
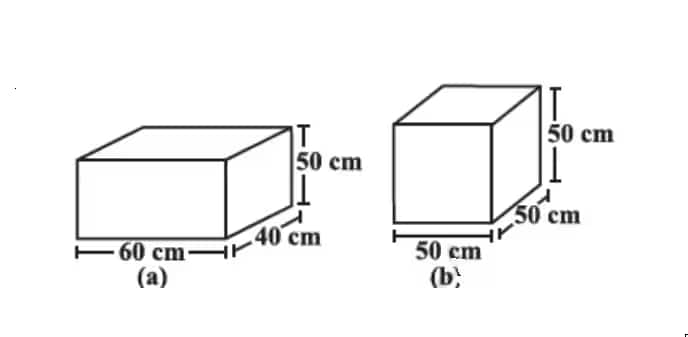
![]()
Answer:
Surface area of cuboid (a) =2(60×40+40×50+50×60)=14800 cm2
Surface area of cube (b) =6(50)2=15000 cm2
So, box (a) requires the lesser amount of material to make.
Answer:
Surface area of suitcase =2(80×48+48×24+24×80) = 13824 cm2 .
The area of such 100 suitcases will be 1382400 cm2
So length of tarpaulin cloth $= \frac{1382400}{96}$ cm = 14400 cm or 144 m
Question 3: Find the side of a cube whose surface area is 600 cm2.
Answer:
Surface area of cube = 6l2
So, 6l2 = 600
⇒ l2 = 100
⇒ l = 10 cm
Thus, the side of the cube is 10 cm.
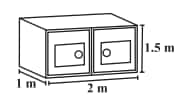
![]()
Answer:
Required area = Total area - Area of bottom surface
Total area =2(1×2+2×1.5+1.5×1) = 13 m2
Area of bottom surface = 1×2 = 2 m2
So, required area = 13−2 =11 m2
Answer:
Total area painted by Daniel :
= 2(15×10+10×7+7×15) − (15×10) ( ∵ Bottom surface is excluded.)
So, Area
= 650−150 = 500 m2
Number of cans of paint required
$= \frac{500}{100}$
$ = 5$
Thus, 5 cans of paint are required.
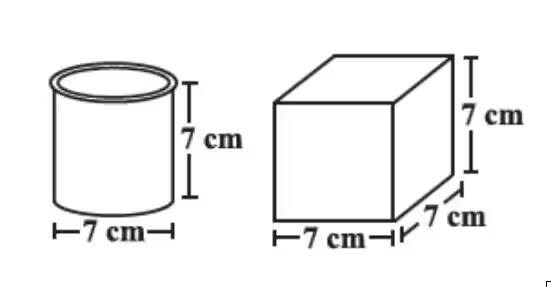
![]()
Answer:
The two figures have the same height. The difference between them is that one is a cylinder and another is a cube.
Lateral surface area of a cylinder
= 2×π×r×h
= 2×π×3.5×7
= 154 cm2
Lateral surface area of a cube
= 4 × side2
= 4×72
= 4×49
= 196 cm2
So, the cube has a larger lateral surface area.
Answer:
Total surface area of a cylinder
= 2πr (h + r)
= 2π×7(7+3)
= 14π×10
= 440 m2
Answer:
Length of rectangular sheet
$= \frac{4224}{33}$
=128 cm
So the perimeter of a rectangular sheet
= 2(l + b)
= 2(128+33)
= 322 cm
Thus perimeter of the rectangular sheet is 322 cm.
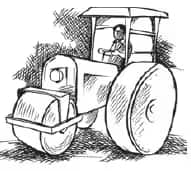
![]()
Answer:
Area in one complete revolution of the roller
= 2πrh
= 2π×0.42×1
= 2.638 m2
So, area of road = 2.638 m2 × 750 = 1978.5 m2
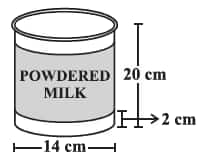
![]()
Answer:
Area of label
= 2πrh
=2π×(7)×(16)
=703.71 cm2
Here, the height is found out as = 20-2-2 = 16 cm.
| Class 8 maths chapter 9 NCERT solutions: Exercise 9.3 Total Questions: 8 Page number: 119-120 |
Question 1: Given a cylindrical tank, in which situation will you find surface area and in
Which situation volume?
(a) To find how much it can hold.
Answer:
(a) To find out how much the cylindrical tank can hold, we will basically find out the volume of the cylinder.
Question 1: Given a cylindrical tank, in which situation will you find surface area and in
which situation volume?
(b) Number of cement bags required to plaster it.
Answer:
(b) If we want to find out the cement bags required to plaster, it means the area to be applied, and we then calculate the surface area of the bags.
Question 1: Given a cylindrical tank, in which situation will you find surface area and in
Which situation volume?
(c) To find the number of smaller tanks that can be filled with water from it.
Answer:
(c) We have to find out the volume.

![]()
Answer:
Given the diameter of cylinder A = 7 cm and the height = 14 cm.
Also, the diameter of cylinder B = 14 cm and its height = 7 cm.
We can easily suggest whose volume is greater without doing any calculations:
Volume is directly proportional to the square of the radius of the cylinder and directly proportional to the height of the cylinder.
Hence,
B has more Volume as compared to A because B has a larger diameter.
Verifying:
Volume of A : π×r2×height=π × $(\frac72)^2$ ×14cm = 539 cm3
and Volume of B : π×r2×height=π×($\frac{14}2$)2×7cm=1,078 cm3
Hence, clearly we can see that the volume of cylinder B is greater than the volume of cylinder A.
The cylinder B has surface area of = 2×π×r(r+h)=2×π× $\frac{14}{2}$ ($\frac{14}{2}$+7) = 616 cm2 .
and the surface area of cylinder A = 2×π×r(r+h)=2×π×$\frac72$×($\frac72$+14) = 385 cm2 .
The cylinder with greater volume also has greater surface area.
Question 3: Find the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3.
Answer:
Given the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3
As the Volume of the cuboid = base area × height
So, we have the relation: 900 cm3 = 180cm2 × height
⇒ Height = 5 cm
Answer:
So given the dimensions of a cuboid are 60 cm × 54 cm × 30 cm
Hence, its volume is equal to = 97,200 cm3
We have to make small cubes with a side of 6 cm, which occupy the volume
= 6 cm × 6 cm × 6 cm = 216 cm3
Hence, we now have one cube having a side length = 6 cm and volume = 216 cm3
So, the total number of small cubes that can be placed in the given cuboid
= $\frac{97200}{216}=450$
Hence, 450 small cubes can be placed in that cuboid.
Question 5: Find the height of the cylinder whose volume is 1.54 m 3 and diameter of the base is 140 cm?
Answer:
Given that the volume of the cylinder is 1.54 m3 and its diameter at the base = 140 cm
So, as the Volume of the cylinder = base area × height
Hence, putting in the relation, we get;
1.54 m3 = (π× (1.4 m2)2) × height
The height of the cylinder would be = 1 metre
Answer:
Volume of the cylinder = V = πr2h = π(1.5)2×7 = 49.48 m3
So, the quantity of milk in litres that can be stored in the tank is 49500 litres.
(∵1 m3 = 1000 litres)
Question 7(i): If each edge of a cube is doubled, how many times will its surface area increase?
Answer:
The surface area of a cube = 6l2
So if we double the edge, l becomes 2l.
New surface area = 6(2l)2 = 24l2
Thus surface area becomes 4 times.
Question 7 (ii): If each edge of a cube is doubled, how many times will its volume increase?
Answer:
Volume of cube = l3
Since l becomes 2l, so new volume is : (2l)3 = 8l3
Hence, the volume becomes 8 times.
Answer:
Given that the water is pouring into a cuboidal reservoir at the rate of 60 litres per minute.
The volume of the reservoir is 108 m3, then
The number of hours it will take to fill the reservoir will be:
As we know, 1 m3 = 1000L
Then 108 m3 = 108,000 Litres
Time taken to fill the tank will be:
$\frac{108000}{60}$ =1800 minutes
1800 minutes = $\frac{1800}{60}$ = 30 hours
Mensuration Class 8 Chapter 9: Topics
The topics discussed in the NCERT Solutions for class 8, chapter 9, Mensuration, are:
- Introduction
- Area of a Polygon
- Solid Shapes
- Surface Area of Cube, Cuboid and Cylinder
- Volume of Cube, Cuboid and Cylinder
- Volume and Capacity
Mensuration Class 8 Solutions - Important Formulae
Perimeter Formulae
| Figure | Formula |
|---|---|
| General Perimeter | Length of the outline of a simple closed figure |
| Rectangle | $2 \times (\text{Length} + \text{Breadth})$ |
| Square | $4 \times \text{Side}$ |
| Circle (Circumference) | $2\pi r$ (where r = radius) |
| Parallelogram | $2 \times (\text{Base} + \text{Height})$ |
| Triangle | a + b + c (where a,b,c = sides) |
| Trapezium | a + b + c + d (all sides) |
| Kite | 2a + 2b (where a,b = pairs of adjacent sides) |
| Rhombus | $4 \times \text{Side}$ |
| Hexagon | $6 \times \text{Side}$ |
Surface Area Formula
| Figure | Formula |
|---|---|
| Curved Surface Area of a Cone | $\pi r l$ where $l = \sqrt{r^2 + h^2}$ |
Volume Formulae
| Figure | Formula |
|---|---|
| Cuboid | $\text{Length} \times \text{Breadth} \times \text{Height}$ |
| Cone | $\frac{1}{3} \pi r^2 h$ |
| Sphere | $\frac{4}{3} \pi r^3$ |
| Hemisphere | $\frac{2}{3} \pi r^3$ |
NCERT Solutions for Class 8 Maths: Chapter Wise
The links below allow students to access all the Maths solutions from the NCERT book.
NCERT Solutions for Class 8: Subject Wise
Students can use the following links to find the solutions for other subjects.
NCERT Books and NCERT Syllabus
During preparation, one of the most important tools is the latest syllabus. The following link will lead you to it. There are also links for some reference books, which are beneficial for students.
Popular Questions
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters