NCERT Solutions for Exercise 11.2 Class 10 Maths Chapter 11 - Constructions
NCERT Solutions For Class 10 Maths Chapter 11 Exercise 11.2
NCERT Solutions for Exercise 11.2 Class 10 Maths Chapter 11 Constructions are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 11.2 consists of descriptive points of creating circles in a logical way, with justification. Also, some properties and technical terms of special conic curves. This chapter contains important concepts to understand in two-dimensional geometry. starts with the construction of a circle under certain given conditions ie measurement of radius, a distance of a point from the start of tracing tangents and chords briefly covered in this chapter and mentioned question somehow is like the foundation of the examination, are indeed a major element to cover thoroughly.
10th class Maths exercise 11.2 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.
Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 11 exercise 11.2
Assess NCERT Solutions for Class 10 Maths chapter 11 exercise 11.2
Constructions Class 10 Chapter 11 Exercise: 11.2
Q1 In each of the following, give also the justification of the construction:
Draw a circle of radius 6 cm. From a point 10 cm away from its center, construct the pair of tangents to the circle and measure their lengths.
Answer:
Steps of construction:-
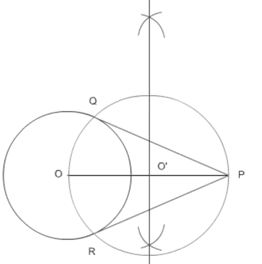
(i) Taking point O as center draw a circle of radius 6 cm.
(ii) Now, name a point P which is 10 cm away from point O. Join OP.
(iii) Draw a perpendicular bisector of OP name the intersection point of bisector and OP as O'.
(iv) Now draw a circle considering O' as center and O'P as the radius.
(v) Name the intersection point of circles as Q and R.
(vi) Join PQ and PR. These are the required tangents.
(vii) Measure lengths of PQ = 8cm and PR = 8cm
Answer:
Steps of constructions:-
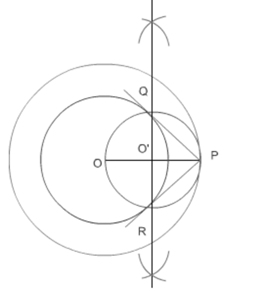
(i) Taking point O as a center draw a circle of radius 4 cm.
(ii) Now taking O as center draw a concentric circle of radius 6 cm.
(iii) Taking any point P on the outer circle, join OP.
(iv) Draw a perpendicular bisector of OP.
(v) Name the intersection of bisector and OP as O'.
(vi) Now, draw a circle taking O' as center and O'P as the radius.
(vii) Name the intersection point of two circles as R and Q.
(viii) Join PR and PQ. These are the required tangents.
(ix) Measure the lengths of the tangents. PR = 4.47 cm and PQ = 4.47 cm.
Answer:
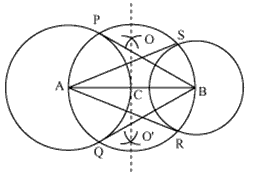
Steps of construction:-
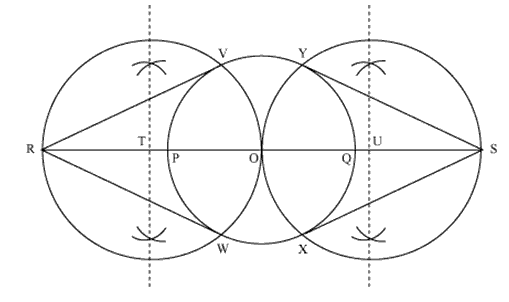
(i) Taking O as a center draw a circle of radius 3 cm.
(ii) Now draw a diameter PQ of this circle and extend it.
(iii) Mark two points R and S on the extended diameter such that OR = OS = 7 cm.
(iv) Draw the perpendicular bisector of both the lines and name their mid-points as T and U.
(v) Now, taking T and U as center draw circles of radius TR and QS.
(vi) Name the intersecting points of the circles with the first circles as V, W, X, Y.
(vii) Join the lines. These are the required tangents.
Answer:
Steps of construction:-
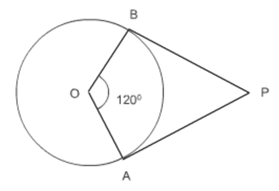
(i) Draw a circle with center O and radius 5 cm.
(ii) Now mark a point A on the circumference of the circle. And draw a line AP perpendicular to the radius OA.
(iii) Mark a point B on the circumference of the circle such that $\angle$ AOB = 120 o . (As we know, the angle at the center is double that of the angle made by tangents).
(iv) Join B to point P.
(v) AP and BP are the required tangents.
Answer:
Steps of construction:-
(i) Draw a line segment AB having a length of 8 cm.
(ii) Now, taking A as a center draw a circle of radius 4 cm. And taking B as a center draw a circle of radius 3 cm.
(iii) Bisect the line AB and name the mid-point as C.
(iv) Taking C as a center and AC as radius draw a circle.
(v) Name the intersection points of the circle as P, Q, R, S.
(vi) Join the lines and these are our required tangents.
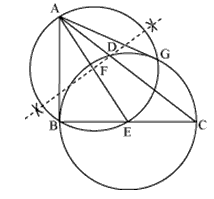
Answer:
Steps of construction:-
(i) Draw a line segment BC of length 8 cm.
(ii) Construct a right angle at point B. Now draw a line of length 6 cm. Name the other point as A.
(iii) Join AC. $\Delta$ ABC is the required triangle.
(iv) Now construct a line BD on the line segment AC such that BD is perpendicular to AC.
(v) Now draw a circle taking E as a center (E is the midpoint of line BC) and BE as the radius.
(vi) Join AE. And draw a perpendicular bisector of this line.
(vii) Name the midpoint of AE as F.
(viii) Now, draw a circle with F as center and AF as the radius.
(ix) Name the intersection point of both the circles as G.
(x) Join AG. Thus AB and AG are the required tangents.
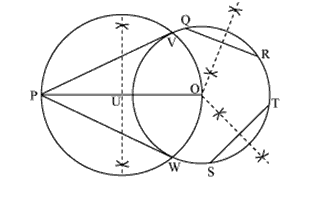
Answer:
Steps of construction:-
(i) Draw a circle using a bangle.
(ii) Now draw 2 chords of this circle as QR and ST.
(iii) Take a point P outside the circle.
(iv) Draw perpendicular bisector of both the chords and let them meet at point O.
(v) Joinpoint PO.
(vi) Draw bisector of PO and name the midpoint as U.
(vii) Now, taking U as a center and UP as radius draw a circle.
(viii) Name the intersection point of both the circles as V and W.
(ix) Join PV and PW. These are the required tangents.
More About NCERT Solutions for Class 10 Maths Chapter 11 Exercise 11.2
The problems from the theory point of view are covered in exercise 11.2 Class 10 Maths. The Initial questions of NCERT solutions for Class 10 Maths chapter 11 exercise 11.2 is to construct figures using protractors and dividers. And later on questions of Class 10 Maths chapter 11 exercise, 11.2 is to prove based on fundamental properties of Circle and tangents attached to it. In NCERT syllabus Class 10 Maths chapter 11 exercise 11.2 also covers some exclusive problems on triple circle scenarios with chords.
Also Read| Constructions Class 10 Notes
Also, see-
NCERT Solutions Subject Wise
Frequently Asked Questions (FAQs)
The Minimum of 3 points is required to construct a circle from scratch.
The Sum of all the angles for the above-mentioned condition is 360 degrees.
Ans: We have to draw/construct diagrams of curves using dark pointed pencils in order to get good marks.
Ans: Yes we can prove theorems with constructions, in fact, students will find some questions related to it.
Questions related to CBSE Class 10th
On Question asked by student community
HELLO,
I am attaching the link through which you can download and access the Bangalore Sahodaya Class 10th CBSE question paper of Mathematics ( Basic )
Here is the link :- https://school.careers360.com/download/ebooks/bangalore-sahodaya-class-10-mathematics-basic-question-paper-2025-26
It will help you to practice basic level numerical questions, strengthen fundamentals and prepare confidently for the board
HELLO,
Below i am attaching the direct link of Careers360 through which you can download the Bangalore Sahodaya Class 10th Mathematics Basic Question paper 2025 2026
Here is the link :- https://school.careers360.com/download/ebooks/bangalore-sahodaya-class-10-mathematics-basic-question-paper-2025-26
Hope this will help you!
Hello
You will be able to download the CBSE Class 10th Maths Sample Paper 2025-26 using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-10th-maths-sample-papers-2025-26
I hope this information helps you.
Thank you.
Hello,
Here you can access the last 5 years CBSE Class 10 Board Exam Question Papers from the mentioned link below:
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers-class-10
Hope it helps.
You can check the Class 11 English half yearly question paper and answer key for 2025 26 on the Careers360 website. These papers help students practice, understand the exam pattern, and check their answers for better preparation.
You can visit this Careers360 link to access the English question paper and
Popular CBSE Class 10th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
