NCERT Solutions for Class 8 Maths Chapter 1 - A Square and A Cube
In the world of Mathematics, understanding squares and cubes is like finding the secret code to unlock patterns. The amazing journey of learning interesting mathematical concepts starts with Class 8 Maths NCERT Chapter 1: A Square and A Cube. Following the National Education Policy (NEP) 2020 and the National Curriculum Framework for School Education (NCF-SE) 2023, the new book of class 8 Maths is a combination of logic, fun and the history of mathematics. In this chapter, students will solve problems relating to square & cubic numbers, square & cube roots, and their properties. The primary objective of these NCERT Solutions for Class 8 is to provide students with essential study material as they attempt to solve exercises on their own.
This Story also Contains
- NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Download Free PDF
- NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Exercise Questions
- NCERT A Square and A Cube Class 8 Chapter 1: Topics
- Class 8 Maths Chapter 1 A Square and A Cube Solutions: Extra Question
- NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Notes
- NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Points to Remember
- Why are Class 8 Maths Chapter 1 A Square and A Cube Question Answers Important?
- NCERT Solutions for Class 8 Mathematics Chapter Wise
- NCERT Books and NCERT Syllabus

Squares and cubes help students build a strong foundation in the field of Mathematics. Careers360 experts have prepared these NCERT Solutions for Class 8 Maths to make learning easier and help you do better in class and exams. Many toppers rely on NCERT Solutions because they are designed in accordance with the latest syllabus. This article also contains some important notes and formulas, in the hope that students can review them once they have checked these solutions. To access the syllabus, notes, and PDF, check out this NCERT article.
NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Download Free PDF
Careers360 brings you NCERT Class 8 Maths Chapter 1 A Square and A Cube solutions, carefully prepared by subject experts to simplify your studies and help in exams. A downloadable PDF is available — click the link below to access it.
NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Exercise Questions
Here are the NCERT Class 8 Maths Chapter 1 A Square and A Cube question answers with clear and detailed solutions.
|
A Square and A Cube Class 8 Question answers |
Question 1. Which of the following numbers are not perfect squares?
(i) 2032
(ii) 2048
(iii) 1027
(iv) 1089
Answer:
(i)
2032 = 2 × 2 × 2 × 2 × 127
So, 2032 is not a perfect square as 127 has no pair.
(ii)
2048 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
So, 2048 is not a perfect square as the last 2 has no pair.
(iii)
1027 = 13 × 79
So, 1027 is not a perfect square as 13 and 79 have no pairs.
(iv)
1089 = 3 × 3 × 11 × 11
So, 1089 is a perfect square as 3 and 11 both have pairs.
Question 2. Which one among $64^2, 108^2, 292^2, 36^2$ has the last digit 4?
Answer:
$\begin{aligned} & 64^2=4096 \rightarrow \text { ends with } 6 \\ & 108^2=11664 \rightarrow \text { ends with } 4 \\ & 292^2=85264 \rightarrow \text { ends with } 4 \\ & 36^2=1296 \rightarrow \text { ends with } 6\end{aligned}$
So, 1082 and 2922 have 4 as the last digit.
Question 3. Given $125^2=15625$, what is the value of $126^2$?
(i) $15625+126$
(ii) $15625+26^2$
(iii) $15625+253$
(iv) $15625+251$
(v) $15625+51^2$
Answer:
We know, $(a+1)^2=a^2+2a+1$
Here, $a=125$
So, $(125+1)^2= 125^2+2\times125\times1 +1^2=15625+251$
Hence, the correct answer is option (iv).
Question 4. Find the length of the side of a square whose area is $441 \mathrm{~m}^2$.
Answer:
We know that the Area of a square = Side × Side
Here, 441 = 21 × 21
So, the side of the square is 21 m.
Question 5. Find the smallest square number that is divisible by each of the following numbers: 4, 9, and 10.
Answer:
LCM of 4,9, and $10=180$
Prime factorisation of $180=2^2 \times 3^2 \times 5$
To make a perfect square, 5 needs to appear twice.
So, $180 \times 5=900=(30)^2$
Hence, the correct answer is 30.
Question 6. Find the smallest number by which 9408 must be multiplied so that the product is a perfect square. Find the square root of the product.
Answer:
Prime factorisation of $9408=2^6 \times 3 \times 7^2$
To make a perfect square, we need one more 3.
Number becomes
$= 9408 \times 3=28224=2^6 \times 3^2 \times 7^2$
Hence, the square root of 2560320 $=2^3\times3\times7=168$
Question 7. How many numbers lie between the squares of the following numbers?
(i) 16 and 17
(ii) 99 and 100
Answer:
(i) Between $16^2=256$ and $17^2=289$ :
Numbers lie between $=289-256-1=32$
(ii) Between $99^2=9801$ and $100^2=10000$ :
Numbers lie between $=10000-9801-1=198$
Question 8. In the following pattern, fill in the missing numbers:
$1^2+2^2+2^2=3^2$
$2^2+3^2+6^2=7^2 \\$
$3^2+4^2+12^2=13^2 \\$
$4^2+5^2+20^2=()^2 \\$
$9^2+10^2+()^2=()^2$
Answer:
$4^2+5^2+20^2=16+25+400=441=21^2$
So, $4^2+5^2+20^2=(21)^2$
$9^2+10^2=81+100=181$
If we add $90^2+181=8281=91^2$
So, $9^2+10^2+(90)^2=(91)^2$
Question 9. How many tiny squares are there in the following picture? Write the prime factorisation of the number of tiny squares

Answer:
There are 81 tiny squares.
Prime factorisation of 81 = 3 × 3 × 3 × 3 = 34
|
A Square and A Cube Class 8 Question answers |
Question 1. Find the cube roots of 27000 and 10648.
Answer:
Prime factorisation of 27000 = 3 × 3 × 3 × 10 × 10 × 10 = 33 × 103
Hence, the cube root of 27000 = 3 × 10 = 30
Prime factorisation of 10648 = 2 × 2 × 2 × 11 × 11 × 11 = 23 × 113
Hence, the cube root of 10648 = 2 × 11 = 22
Question 2. What number will you multiply by 1323 to make it a cube number?
Answer:
$1323=3^3 \times 7^2$
To make it a perfect cube, we need one more 7 to make 73.
Hence, the answer is 3.
Question 3. State true or false. Explain your reasoning.
(i) The cube of any odd number is even.
(ii) There is no perfect cube that ends with 8.
(iii) The cube of a 2-digit number may be a 3-digit number.
(iv) The cube of a 2-digit number may have seven or more digits.
(v) Cube numbers have an odd number of factors.
Answer:
(i) The cube of any odd number is even.
This statement is False.
Odd $\times$ Odd $\times$ Odd $=$ Odd
Example: $3^3=27$ (odd)
(ii) There is no perfect cube that ends with 8.
This statement is False
Example: $2^3=8$, ends with 8
(iii) The cube of a 2-digit number may be a 3-digit number.
This statement is True.
Example: $10^3=1000$, which is a three-digit number
(iv) The cube of a 2-digit number may have seven or more digits.
This statement is False.
The largest two-digit number is 99.
Try $99^3=970299 \rightarrow$, which is 6 digits
(v) Cube numbers have an odd number of factors.
This statement is False.
Only perfect squares have an odd number of factors.
Example: $8=2^3 \rightarrow$ Factors $=1,2,4,8 \rightarrow 4$ factors (even)
Question 4. You are told that 1331 is a perfect cube. Can you guess without factorisation what its cube root is? Similarly, guess the cube roots of 4913, 12167, and 32768.
Answer:
Cube Root of 1331:
Ends in $1 \rightarrow$ Cube of a number ending in 1 also ends in 1.
Try: $11^3=1331$
So, Cube root of $1331=11$
Cube Root of 4913:
Ends in $3 \rightarrow$ Cube of a number ending in 7 ends in 3.
(because $7^3=343$ )
Try: $17^3=4913$
So, Cube root of $4913=17$
Cube Root of 12167:
Ends in $7 \rightarrow$ Cube of a number ending in 3 ends in 7 (because $3^3=27$ )
Try: $23^3=12167$
So, Cube root of $12167=23$
Cube Root of 32768:
Ends in $8 \rightarrow$ Cube of a number ending in 2 ends in 8.
Try: $32^3=32768$
So, Cube root of $32768=32$
Question 5. Which of the following is the greatest? Explain your reasoning.
(i) $67^3-66^3$
(ii) $43^3-42^3$
(iii) $67^2-66^2$
(iv) $43^2-42^2$
Answer:
We know that $a^3-b^3=(a-b)\left(a^2+a b+b^2\right)$
In the first two options,
(i) $67^3-66^3=(67-66)(67^2+67\times66+66^2)=13267$
(ii) $43^3-42^3=(43-42)(43^2+43\times43+42^2)=5420$
We know that $a^2-b^2=(a+b)(a-b)$
In the last two options,
(iii) $67^2-66^2=(67+66)(67-66)=133$
(iv) $43^2-42^2=(43+42)(43-42)=85$
Hence, $67^3-66^3$ is the greatest.
NCERT A Square and A Cube Class 8 Chapter 1: Topics
The topics discussed in the NCERT Solutions for Class 8 Chapter 1 A Square and A Cube are:
- Introduction
- Square Numbers
- Patterns and Properties of Perfect Squares
- Perfect Squares and Odd Numbers
- Perfect Squares and Triangular Numbers
- Square Roots
- Cubic Numbers
- Taxicab Numbers
- Perfect Cubes and Consecutive Odd Numbers
- Cube Roots
- Successive Differences
- A Pinch of History
Class 8 Maths Chapter 1 A Square and A Cube Solutions: Extra Question
Question:
Simplify the following.
$\frac{\sqrt{10+\sqrt{25+\sqrt{108+\sqrt{154+\sqrt{225}}}}}}{\sqrt{16+19.25 \times 4^2}}$
Solution:
$\frac{\sqrt{10+\sqrt{25+\sqrt{108+\sqrt{154+\sqrt{225}}}}}}{\sqrt{16+19.25 \times 4^2}}$
$=\frac{\sqrt{10+\sqrt{25+\sqrt{108+\sqrt{154+15}}}}}{\sqrt{4^2(1+19.25)}}$
$=\frac{\sqrt{10+\sqrt{25+\sqrt{108+13}}}}{4\sqrt{20.25}}$
$=\frac{\sqrt{10+\sqrt{25+11}}}{4\ \times 4.5}$
$=\frac{\sqrt{10+6}}{18}$
$=\frac{4}{18}$
$=\frac{2}{9}$
Hence, the correct answer is $\frac{2}{9}$.
NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Notes
Careers360 has prepared these A Square and A Cube Notes to make your revision smoother and faster. Additionally, these notes will help students to understand the A Square and A Cube class 8 solutions and solve them on their own from next time.
Square Numbers and Perfect Squares
A number obtained by multiplying a number by itself is called a square number. Squares of natural numbers are called perfect squares.
Example: 2 × 2 = 4, it is a perfect square.
Properties of Perfect Squares
-
Non-Negative Perfect Squares:
Perfect squares are always non-negative numbers.
If we multiply two negative numbers, we will get a positive number all the time.
(Example: –8 × –8 = +64)
Or, if we multiply two positive numbers, the resultant number is always positive.
(Example: +8 × +8 = +64).
-
Square Root of a Perfect Square:
The square root of a perfect square is always an integer.
Example: $\sqrt9=3$, which is an integer, $\sqrt{121}=11$, which is an integer
-
Last digit of a Perfect Square:
Most of the time, Perfect squares end with the integers 0, 1, 4, 5, 6, or 9, but never in 2, 3, 7, or 8, when expressed in the base 10.
Example: 100(102), 121(112), 144(122), 225(152), 196(142), 169(132),...
Cubes and Perfect Cubes
In general, we heard about the word “Cube” in Geometry. A cube is a solid figure all of whose sides meet at right angles and are equal.
A number obtained by multiplying a number by itself three times is called a cube or a cubic number. A number is a perfect cube if its prime factors can be split into three identical groups.
Example: 2 × 2 × 2 = 8, it is a perfect cube.

Properties of Perfect Cubes
-
Positive and Negative Perfect Cubes
Perfect cubes can be positive or negative integers, unlike perfect squares, which are always non-negative integers.
Example: −27 is a perfect cube as −27 = (−3)3
-
Cube root of a Perfect Cube
The cube root of a perfect cube is always an integer.
Example: $\sqrt[3]{9}=3$, which is an integer, $\sqrt[3]{64}=4$, which is an integer
-
Last digit of a Perfect Cube
In base 10, a perfect cube can end in any digit, unlike perfect squares, which have more restricted ending digits.
Example: 343(73), 512(83), 1728(123), 2197(133)
In these examples, the perfect cube ending digits are 3, 2, 8, 7. These digits do not generally come up at the end of a perfect square.
Square roots and Cube roots
The symbol $\sqrt{}$ denotes the square root.
For example, $\sqrt{16}=4$
The symbol $\sqrt[3]{}$ denotes the cube root.
For example, $\sqrt[3]{64}=4$.
Prime Factorisation Method
The most common method to find the square root of a perfect square is:
- Prime factorisation method
The prime factorisation of a perfect square provides insight into its factors. All the exponents in its prime factorisation must be even in a perfect square.
Here are the steps to use the prime factorisation method.
Step 1: Factorise the number into its prime factors.
Step 2: Pair the same type of prime factors.
Step 3: Multiply one number from each pair to get the required square root.
Example:
The prime factors of 225 = 3 × 3 × 5 × 5 = 32 × 52
Taking one number from each pair, we get 3 × 5 =15
So, the square root of 225 is 15.
There are two other methods, which we will learn in later classes.
- Long division method
- Estimation method
Below, you can find a list of a few squares and cubes.
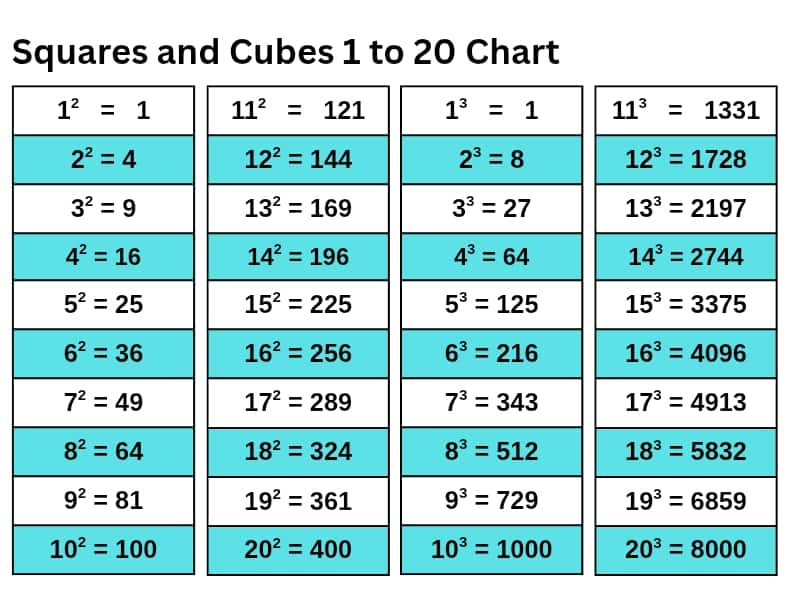
Taxicab Numbers
Numbers that can be expressed as the sum of two cubes in two different ways are called taxicab numbers.
1729 is the first taxicab number
$1729=1^3+12^3=9^3+10^3$
Also, 4104 is a taxicab number.
$4104=2^3+16^3=9^3+15^3$
13832 is a taxicab number.
$13832=2^3+24^3=18^3+20^3$
People also know 1729 as the Hardy–Ramanujan Number, and it was named after the renowned Indian mathematician Srinivasa Ramanujan and the British mathematician Godfrey Harold Hardy.

NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube: Points to Remember
Here are some points that will help students while practising the solutions of the A Square and A Cube Class 8 chapter.
- The square of a number is denoted as n2, where n is the number.
- A number which is the square of an integer is called a perfect square.
- We can get the square root of a number when multiplied by itself, which gives the original number.
- The prime factorisation method is the best way to check if a number is a perfect square or a perfect cube.
Factorise the numbers into their prime factors.
1. If the exponents of the numbers in the factorisation are even, then it's a perfect square.
2. If the exponents of the numbers in the factorisation are a multiple of 3, then it's a perfect cube. - A number can be both a perfect square and a perfect cube. For example: 64, 729, etc
- The square of a number ending with 1, 4, 5, 6, or 9 always ends in the same digit as the number.
- The square of a negative number is also positive, but the cube of a negative number is always negative.
- The difference between consecutive perfect squares gives the sequence of odd numbers.
Why are Class 8 Maths Chapter 1 A Square and A Cube Question Answers Important?
Understanding the question answers of Chapter 1 of Class 8 Maths, A Square and A Cube, is very important because it builds a strong base for higher-level maths. This chapter teaches useful tricks, patterns, and number properties that help students calculate faster and solve questions easily. It also improves logical thinking and problem-solving skills, which are needed in many other chapters, like algebra and number systems. Class 8 Maths chapter 1 A Square and A Cube question answers also become easier to understand because of the concepts learned here. Here are some more important points why you should check these question answers.
- These solutions help students understand square numbers, cube numbers, their properties, and patterns clearly, which are used in many maths problems.
- Learning square roots and cube roots improves calculation speed and makes mental maths faster.
- These concepts are helpful in higher classes, such as Class 9 and Class 10, where topics like polynomials, geometry, and equations use squares and cubes.
NCERT Solutions for Class 8 Mathematics Chapter Wise
We at Careers360 compiled all the NCERT class 8 Maths solutions in one place for easy student reference. The following links will allow you to access them.
|
NCERT Solutions for Class 8 Maths Chapter 1 A Square and A Cube |
|
NCERT Solutions for Class 8 Maths Chapter 3 A Story of Numbers |
|
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply |
|
NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning-1 |
NCERT Books and NCERT Syllabus
The following links will give students access to the latest NCERT syllabus and some reference books.
Frequently Asked Questions (FAQs)
Some triangular numbers can also be perfect squares.
For example, 36 is both a triangular number and a perfect square, showing the connection between geometric patterns and number properties.
A Taxicab number is the smallest number expressible as the sum of two positive cubes in two different ways.
For example,
1729 = 1³ + 12³ = 9³ + 10³
This chapter covers the following key topics:
Properties of square numbers and cube numbers
Patterns of squares and cubes
Finding squares and cubes of numbers
Perfect Squares and Odd Numbers
Perfect Squares and Triangular Numbers
Square roots and cube roots
Perfect Cubes and Consecutive Odd Numbers
Solving problems related to squares and cubes in real life
Many educational platforms, such as Careers360, offer free downloadable PDFs of Class 8 A Square and A Cube solutions. Students can find the free downloadable PDF in this article itself.
We can use the Prime Factorisation method to find cube roots of numbers.
First, divide the number into prime factors.
Group them in triplets to find the cube root of the number.
Here are some real-life uses of squares and cubes.
Squares are used in calculating areas of square and rectangular fields, tiles, or plots.
Cubes are useful in finding the volume of cubes or cuboids, such as water tanks and storage boxes.
Here are some methods which we can use to find square roots.
Prime Factorisation Method
Division Method
Estimation Method
Here are some tricks students can use to learn squares and cubes easily.
Memorise squares up to 30 and cubes up to 20 for quick calculations.
Practice the patterns of numbers
Solve the exercises in the NCERT textbook questions regularly
Use the factorisation method to find square roots and cube roots quickly
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
