Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 11 Maths Chapter 8 Binomial Theorem

NCERT Solutions for Class 11 Maths Chapter 8 Binomial Theorem

Edited By Ramraj Saini | Updated on Sep 23, 2023 06:17 PM IST

Binomial Theorem Class 11 Questions And Answers

NCERT Solutions for Class 11 Maths Chapter 8 Binomial Theorem are provided here. These NCERT solutions are prepared by subjects matter experts considering the latest syllabus and pattern of CBSE 2023-24. You have studied the expansion of expressions like (a-b)2 and (a-b)3 in the previous classes. So you can calculate numbers like (96)3. If the power is high, it will be difficult to use normal multiplication. How will you process in such cases? In the class 11 maths chapter 8 NCERT solutions, you will get the answer to the above question. In this NCERT Book chapter, you will study the expansion of (a+b)n, the general terms of the expansion, the middle term of the expansion, and the pascal triangle.

This Story also Contains
  1. Binomial Theorem Class 11 Questions And Answers
  2. Binomial Theorem Class 11 Questions And Answers PDF Free Download
  3. Binomial Theorem Class 11 Solutions - Important Formulae
  4. Binomial Theorem Class 11 NCERT Solutions (Intext Questions and Exercise)
  5. Highlights of NCERT Solutions for Class 11 Maths Chapter 8 – Binomial Theorem
  6. Key Features of NCERT Solutions for Class 11 Maths Chapter 8 – Binomial Theorem
NCERT Solutions for Class 11 Maths Chapter 8 Binomial Theorem
NCERT Solutions for Class 11 Maths Chapter 8 Binomial Theorem

In NCERT solutions for class 11 chapter 8 binomial theorem, you will get questions related to these topics. NCERT Book this chapter covers the binomial theorem for positive integral indices only. The concepts of a binomial theorem are not only useful in solving problems of mathematics, but in various fields of science too. In the NCERT syllabus of this chapter, there are 26 problems in 2 exercises. All these questions are prepared in binomial theorem class 11 NCERT solutions in a detailed manner. It will be very easy for you to understand the concepts. Check all NCERT solutions from class 6 to 12 to learn science and maths. Here you will get NCERT solutions for class 11 also.

Also read:

Binomial Theorem Class 11 Questions And Answers PDF Free Download

Download PDF

Binomial Theorem Class 11 Solutions - Important Formulae

Binomial Theorem:

The Binomial Theorem provides the expansion of a binomial (a + b) raised to any positive integer n.

The expansion of (a + b)n is given by: (a + b)n = nC0 * an + nC1 * a(n-1) * b + nC2 * a(n-2) * b2 + … + nCn-1 * a * b(n-1) + nCn * bn.

Special Cases from the Binomial Theorem:

(x - y)n = nC0 * xn - nC1 * x(n-1) * y + nC2 * x(n-2) * y2 + … + (-1)n * nCn * x.

(1 - x)n = nC0 - nC1 * x + nC2 * x2 - …. + (-1)n * nCn * xn.

The coefficients nC0 and nCn are always equal to 1.

Pascal’s Triangle:

The coefficients of the expansions in the Binomial Theorem are arranged in an array called Pascal’s triangle.

General Term of Expansions:

For (a + b)n, the general term is T_{r+1} = nCr * a(n-r) * b^r.

For (a - b)n, the general term is (-1)r * nCr * a(n-r) * b^r.

For (1 + x)n, the general term is nCr * xr.

For (1 - x)n, the general term is (-1)^r * nCn * xn.

Middle Terms:

In the expansion (a + b)n, if n is even, then the middle term is the (n/2 + 1)-th term.

If n is odd, then the middle terms are the (n/2 + 1)-th and ((n+1)/2 + 1)-th terms.

Free download NCERT Solutions for Class 11 Maths Chapter 8 Binomial Theorem for CBSE Exam.

Binomial Theorem Class 11 NCERT Solutions (Intext Questions and Exercise)

Binomial theorem class 11 solutions - Exercise 8.1

Question:1 Expand the expression. (1-2x)^5

Answer:

Given,

The Expression:

(1-2x)^5

the expansion of this Expression is,

(1-2x)^5 =

\\^5C_0(1)^5-^5C_1(1)^4(2x)+^5C_2(1)^3(2x)^2-^5C_3(1)^2(2x)^3+^5C_4(1)^1(2x)^4-^5C_5(2x)^5

1-5(2x)+10(4x^2)-10(8x^3)+5(16x^4)-(32x^5)

1-10x+40x^2-80x^3+80x^4-32x^5

Question:2 Expand the expression. \left(\frac{2}{x} - \frac{x}{2} \right )^5

Answer:

Given,

The Expression:

\left(\frac{2}{x} - \frac{x}{2} \right )^5

the expansion of this Expression is,

\left(\frac{2}{x} - \frac{x}{2} \right )^5\Rightarrow

\\^5C_0\left(\frac{2}{x}\right)^5-^5C_1\left(\frac{2}{x}\right)^4\left(\frac{x}{2}\right)+^5C_2\left(\frac{2}{x}\right)^3\left(\frac{x}{2}\right)^2 -^5C_3\left(\frac{2}{x}\right)^2\left(\frac{x}{2}\right)^3+^5C_4\left(\frac{2}{x}\right)^1\left(\frac{x}{2}\right)^4-^5C_5\left(\frac{x}{2}\right)^5

\Rightarrow \frac{32}{x}-5\left ( \frac{16}{x^4} \right )\left ( \frac{x}{2} \right )+10\left ( \frac{8}{x^3} \right )\left ( \frac{x^2}{4} \right )-10\left ( \frac{4}{x^2} \right )\left ( \frac{x^2}{8} \right ) +5\left ( \frac{2}{x} \right )\left ( \frac{x^4}{16} \right )-\frac{x^5}{32}

\Rightarrow \frac{32}{x^5}-\frac{40}{x^3}+\frac{20}{x}-5x+\frac{5x^2}{8}-\frac{x^3}{32}

Question:3 Expand the expression. (2x-3)^6

Answer:

Given,

The Expression:

(2x-3)^6

the expansion of this Expression is,

(2x-3)^6=

\Rightarrow \\^6C_0(2x)^6-^6C_1(2x)^5(3)+^6C_2(2x)^4(3)^2-^6C_3(2x)^3(3)^3+ ^6C_4(2x)^2(3)^4-^6C_5(2x)(3)^5+^6C_6(3)^6

\Rightarrow 64x^6-6(32x^5)(3)+15(16x^4)(9)-20(8x^3)(27)+15(4x^2)(81)-6(2x)(243) +729

\Rightarrow 64x^6-576x^5+2160x^4-4320x^3+4860x^2-2916x+729

Question:4 Expand the expression. \left(\frac{x}{3} + \frac{1}{x} \right )^5

Answer:

Given,

The Expression:

\left(\frac{x}{3} + \frac{1}{x} \right )^5

the expansion of this Expression is,

\left(\frac{x}{3} + \frac{1}{x} \right )^5\Rightarrow

\Rightarrow ^5C_0\left(\frac{x}{3}\right)^5+^5C_1\left(\frac{x}{3}\right)^4\left(\frac{1}{x}\right)+^5C_2\left(\frac{x}{3}\right)^3\left(\frac{1}{x}\right)^2 +^5C_3\left(\frac{x}{3}\right)^2\left(\frac{1}{x}\right)^3+^5C_4\left(\frac{x}{3}\right)^1\left(\frac{1}{x}\right)^4+^5C_5\left(\frac{1}{x}\right)^5

\Rightarrow \frac{x^5}{243} +5\left ( \frac{x^4}{81} \right )\left ( \frac{1}{x} \right )+10\left ( \frac{x^3}{27} \right )\left ( \frac{1}{x^2} \right )+10\left ( \frac{x^2}{9} \right )\left ( \frac{1}{x^3} \right ) +5\left ( \frac{x}{3} \right )\left ( \frac{1}{x^4} \right )+\frac{1}{x^5}

\Rightarrow \frac{x^5}{243}+\frac{5x^3}{81}+\frac{10x}{27}+\frac{10}{9x}+\frac{5}{3x^2}+\frac{1}{x^5}

Question:5 Expand the expression. \left(x + \frac{1}{x} \right )^6

Answer:

Given,

The Expression:

\left(x + \frac{1}{x} \right )^6

the expansion of this Expression is,

\left(x + \frac{1}{x} \right )^6

\Rightarrow ^6C_0(x)^6+^6C_1(x)^5\left ( \frac{1}{x} \right )+^6C_2(x)^4\left ( \frac{1}{x} \right )^2+^6C_3(x)^3\left ( \frac{1}{x} \right )^3+ ^6C_4(x)^2\left ( \frac{1}{x} \right )^4+^6C_5(x)\left ( \frac{1}{x} \right )^5+^6C_6\left ( \frac{1}{x} \right )^6

\Rightarrow x^6+6(x^5)\left ( \frac{1}{x} \right )+15(x^4)\left ( \frac{1}{x^2} \right )+20(8x^3)\left ( \frac{1}{x^3} \right ) +15(x^2)\left ( \frac{1}{x^4} \right )+6(x)\left ( \frac{1}{x^5} \right )+\frac{1}{x^6}

\Rightarrow x^6+6x^4+15x^2+20+\frac{15}{x^2}+\frac{6}{x^4}+\frac{1}{x^6}

Question:6 Using binomial theorem, evaluate the following: (96)^3

Answer:

As 96 can be written as (100-4);

\\\Rightarrow (96)^3\\=(100-4)^3\\=^3C_0(100)^3-^3C_1(100)^2(4)+^3C_2(100)(4)^2-^3C_3(4)^3

\\=(100)^3-3(100)^2(4)+3(100)(4)^2-(4)^3

\\=1000000-120000+4800-64

\\=884736

Question:7 Using binomial theorem, evaluate the following: (102)^5

Answer:

As we can write 102 in the form 100+2

\Rightarrow (102)^5

=(100+2)^5

\\=^5C_0(100)^5+^5C_1(100)^4(2)+^5C_2(100)^3(2)^2 +^5C_3(100)^2(2)^3+^5C_4(100)^1(2)^4+^5C_5(2)^5

=10000000000+1000000000+40000000+800000+8000+32

=11040808032

Question:8 Using binomial theorem, evaluate the following:

(101)^4

Answer:

As we can write 101 in the form 100+1

\Rightarrow (101)^4

=(100+1)^4

\\=^4C_0(100)^4+^4C_1(100)^3(1)+^4C_2(100)^2(1)^2 +^4C_3(100)^1(1)^3+^4C_4(1)^4

=100000000+4000000+60000+400+1

=104060401

Question:9 Using binomial theorem, evaluate the following: (99)^5

Answer:

As we can write 99 in the form 100-1

\Rightarrow (99)^5

=(100-1)^5

\\=^5C_0(100)^5-^5C_1(100)^4(1)+^5C_2(100)^3(1)^2 -^5C_3(100)^2(1)^3+^5C_4(100)^1(1)^4-^5C_5(1)^5

=10000000000-500000000+10000000-100000+500-1

=9509900499

Question:10 Using Binomial Theorem, indicate which number is larger (1.1) 10000 or 1000.

Answer:

AS we can write 1.1 as 1 + 0.1,

(1.1)^{10000}=(1+0.1)^{10000}

=^{10000}C_0+^{10000}C_1(1.1)+Other \:positive\:terms

=1+10000\times1.1+ \:Other\:positive\:term

>1000

Hence,

(1.1)^{10000}>1000

Question:11 Find (a + b)^4 - (a-b)^4 . Hence, evaluate (\sqrt{3} + \sqrt2)^4 - (\sqrt3-\sqrt2)^4 .

Answer:

Using Binomial Theorem, the expressions (a+b)^4 and (a-b)^4 can be expressed as

(a+b)^4=^4C_0a^4+^4C_1a^3b+^4C_2a^2b^2+^4C_3ab^3+^4C_4b^4

(a-b)^4=^4C_0a^4-^4C_1a^3b+^4C_2a^2b^2-^4C_3ab^3+^4C_4b^4

From Here,

(a+b)^4-(a-b)^4 = ^4C_0a^4+^4C_1a^3b+^4C_2a^2b^2+^4C_3ab^3+^4C_4b^4 -^4C_0a^4+^4C_1a^3b-^4C_2a^2b^2+^4C_3ab^3-^4C_4b^4

(a+b)^4-(a-b)^4 = 2\times( ^4C_1a^3b+^4C_3ab^3)

(a+b)^4-(a-b)^4 = 8ab(a^2+b^2)

Now, Using this, we get

(\sqrt{3} + \sqrt2)^4 - (\sqrt3-\sqrt2)^4=8(\sqrt{3})(\sqrt{2})(3+2)=8\times\sqrt{6}\times5=40\sqrt{6}

Question:12 Find (x+1)^6 + (x-1)^6 . Hence or otherwise evaluate (\sqrt2+1)^6 + (\sqrt2-1)^6 .

Answer:

Using Binomial Theorem, the expressions (x+1)^4 and (x-1)^4 can be expressed as ,

(x+1)^6=^6C_0x^6+^6C_1x^51+^6C_2x^41^2+^4C_3x^31^3+^6C_4x^21^4+^6C_5x1^5+^6C_61^6

(x-1)^6=^6C_0x^6-^6C_1x^51+^6C_2x^41^2-^4C_3x^31^3+^6C_4x^21^4-^6C_5x1^5+^6C_61^6

From Here,

\\(x+1)^6-(x-1)^6=^6C_0x^6+^6C_1x^51+^6C_2x^41^2+^4C_3x^31^3+ ^6C_4x^21^4+^6C_5x1^5+^6C_61^6 \:\:\:\:\;\:\:\;\:\:\:\ +^6C_0x^6-^6C_1x^51+^6C_2x^41^2-^4C_3x^31^3+^6C_4x^21^4-^6C_5x1^5+^6C_61^6

(x+1)^6+(x-1)^6=2(^6C_0x^6+^6C_2x^41^2+^6C_4x^21^4+^6C_61^6)

(x+1)^6+(x-1)^6=2(x^6+15x^4+15x^2+1)

Now, Using this, we get

(\sqrt2+1)^6 + (\sqrt2-1)^6=2((\sqrt{2})^6+15(\sqrt{2})^4+15(\sqrt{2})^2+1)

(\sqrt2+1)^6 + (\sqrt2-1)^6=2(8+60+30+1)=2(99)=198

Question:13 Show that 9^{n+1} - 8n - 9 is divisible by 64, whenever n is a positive integer.

Answer:

If we want to prove that 9^{n+1} - 8n - 9 is divisible by 64, then we have to prove that 9^{n+1} - 8n - 9=64k

As we know, from binomial theorem,

(1+x)^m=^mC_0+^mC_1x+^mC_2x^2+^mC_3x^3+....^mC_mx^m

Here putting x = 8 and replacing m by n+1, we get,

9^{n+1}=^{n+1}C_0+\:^{n+1}C_18+^{n+1}C_28^2+.......+^{n+1}C_{n+1}8^{n+1}

9^{n+1}=1+8(n+1)+8^2(^{n+1}C_2+\:^{n+1}C_38+^{n+1}C_48^2+.......+^{n+1}C_{n+1}8^{n-1})

9^{n+1}=1+8n+8+64(k)

Now, Using This,

9^{n+1} - 8n - 9=9+8n+64k-9-8n=64k

Hence

9^{n+1} - 8n - 9 is divisible by 64.

Question:14 Prove that \sum_{r = 0}^n3^r \ ^nC_r = 4^n

Answer:

As we know from Binomial Theorem,

\sum_{r = 0}^na^r \ ^nC_r = (1+a)^n

Here putting a = 3, we get,

\sum_{r = 0}^n3^r \ ^nC_r = (1+3)^n

\sum_{r = 0}^n3^r \ ^nC_r = 4^n

Hence Proved.


Binomial theorem class 11 solutions - Exercise: 8.2

Question:1 Find the coefficient of

x^5 in (x + 3)^8

Answer:

As we know that the (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

Now let's assume x^5 happens in the (r+1)^{th} term of the binomial expansion of (x + 3)^8

So,

T_{r+1}=^8C_rx^{8-r}3^r

On comparing the indices of x we get,

r=3

Hence the coefficient of the x^5 in (x + 3)^8 is

^8C_3\times3^3=\frac{8!}{5!3!}\times 9=\frac{8\times7\times6}{3\times2}\times9=1512

Question:2 Find the coefficient of a^5b^7 in (a- 2b)^{12}

Answer:

As we know that the (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

Now let's assume a^5b^7 happens in the (r+1)^{th} term of the binomial expansion of (a- 2b)^{12}

So,

T_{r+1}=^{12}C_rx^{12-r}(-2b)^r

On comparing the indices of x we get,

r=7

Hence the coefficient of the a^5b^7 in (a- 2b)^{12} is

\\ \Rightarrow ^{12}C_7\times(-2)^7=\frac{12!}{5!7!}\times (-128)\\=\frac{12\times11\times10\times 9\times8}{5\times4\times3\times2}\times(-128) \\=-(729)(128) \\=-101376

Question:3 Write the general term in the expansion of

(x^2 - y)^6

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So the general term of the expansion of (x^2 - y)^6 :

T_{r+1}=^6C_r(x^2)^{6-r}(-y)^r=(-1)^r\times^6C_rx^{12-2r}y^r .

Question:4 Write the general term in the expansion of

(x^2 - xy)^{12}, \ x\neq 0

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So the general term of the expansion of (x^2 - xy)^{12}, is

\\\Rightarrow T_{r+1}\\=^{12}C_r(x^2)^{12-r}(-xy)^r\\=(-1)^r\times^{12}C_rx^{24-2r+r}y^r\\=(-1)^r\times^{12}C_rx^{24-r}y^r .

Question:5 Find the 4 th term in the expansion of (x-2y)^{12} .

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So the 4^{th} term of the expansion of (x-2y)^{12} is

\\\Rightarrow T_4= T_{3+1}\\=^{12}C_3(x)^{12-3}(-2y)^3\\=(-2)^3\times^{12}C_3x^{9}y^3\\=-8\times\frac{12!}{3!9!}x^{9}y^3

\\=-8\times \frac{12\times11\times10}{3\times2}\times x^9y^3\\=-8\times220\times x^9y^3 \\=-1760x^9y^3 .

Question:6 Find the 13 th term in the expansion of \left(9x - \frac{1}{3\sqrt x} \right )^{18},\ x\neq 0

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So the 13^{th} term of the expansion of \left(9x - \frac{1}{3\sqrt x} \right )^{18} is

\\\Rightarrow T_{13}= T_{12+1}\\=^{18}C_{12}(9x)^{18-12}\left(\frac{1}{3\sqrt{x}}\right)^{12}\\ \\ \\=\frac{18!}{12!6!}\times9^{6}\left ( \frac{1}{3} \right )^{12}\times x^{6-6}

\\=\frac{18\times17\times16\times15\times14\times13}{6\times5\times4\times3\times2}\times9^{6}\left ( \frac{1}{3^{12}} \right )

=18564

Question:7 Find the middle terms in the expansion of \left(3 - \frac{x^3}{6} \right )^7

Answer:

As we know that the middle terms in the expansion of (a+b)^n when n is odd are,

\left ( \frac{n+1}{2} \right )^{th}\:term\: \:and\:\:\left ( \frac{n+1}{2}+1 \right )^{th}\:term

Hence the middle term of the expansion \left(3 - \frac{x^3}{6} \right )^7 are

\left ( \frac{7+1}{2} \right )^{th}\:term\: \:and\:\:\left ( \frac{7+1}{2}+1 \right )^{th}\:term

Which are 4^{th}\:term\:and\:\:5^{th} \:term

Now,

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So the 4^{th} term of the expansion of \left(3 - \frac{x^3}{6} \right )^7 is

\\\Rightarrow T_4= T_{3+1}\\=^{7}C_3(3)^{7-3}\left (- \frac{x^3}{6} \right )^3\\=\left ( -\frac{1}{6} \right )^3\times 3^4\times^{7}C_3\times x^{9}\\=\left ( -\frac{1}{6} \right )^3\times 3^4\times\frac{7!}{3!4!}\times x^{9} \\=-\frac{3\times3\times3\times3}{6\times6\times6}\times\frac{7\times 6\times5}{3\times2}\times x^9

=-\frac{105}{8}x^9

And the 5^{th} Term of the expansion of \left(3 - \frac{x^3}{6} \right )^7 is,

\\\Rightarrow T_5= T_{4+1}\\=^{7}C_4(3)^{7-4}\left (- \frac{x^3}{6} \right )^4\\=\left ( -\frac{1}{6} \right )^4\times 3^3\times^{7}C_4\times x^{12}\\=\left ( -\frac{1}{6} \right )^4\times 3^3\times\frac{7!}{3!4!}\times x^{12} \\=\frac{3\times3\times3}{6\times6\times6\times6}\times\frac{7\times 6\times5}{3\times2}\times x^{12}

=\frac{35}{48}x^{12}

Hence the middle terms of the expansion of given expression are

-\frac{105}{8}x^9\:and\:\frac{35}{48}x^{12}.

Question:8 Find the middle terms in the expansion of \left(\frac{x}{3} + 9y \right )^{10}

Answer:

As we know that the middle term in the expansion of (a+b)^n when n is even is,

\left ( \frac{n}{2}+1 \right )^{th}\:term\: ,

Hence the middle term of the expansion \left(\frac{x}{3} + 9y \right )^{10} is,

\left ( \frac{10}{2}+1 \right )^{th}\:term\:

Which is 6^{th}\:term

Now,

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So the 6^{th} term of the expansion of \left(\frac{x}{3} + 9y \right )^{10} is

\\\Rightarrow T_6= T_{5+1}\\=^{10}C_5\left ( \frac{x}{3} \right )^{10-5}\left ( 9y \right )^5\\

=\left ( \frac{1}{3} \right )^5\times9^5\times^{10}C_5\times x^5y^5

=\left ( \frac{1}{3} \right )^5\times9^5\times\left ( \frac{10!}{5!5!} \right )\times x^5y^5

=\left ( \frac{1}{3^5} \right )\times9^5\times\left ( \frac{10\times9\times8\times7\times6}{5\times4\times3\times2} \right )\times x^5y^5

=61236x^5y^5

Hence the middle term of the expansion of \left(\frac{x}{3} + 9y \right )^{10} is nbsp; 61236x^5y^5 .

Question:9 In the expansion of (1 + a)^{m+n} , prove that coefficients of a^m and a^n are equal

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So, the general (r+1)^{th} term T_{r+1} in the binomial expansion of (1 + a)^{m+n} is given by

T_{r+1}=^{m+n}C_r1^{m+n-r}a^r=^{m+n}C_ra^r

Now, as we can see a^m will come when r=m and a^n will come when r=n

So,

Coefficient of a^m :

K_{a^m}=^{m+n}C_m=\frac{(m+n)!}{m!n!}

CoeficientCoefficient of a^n :

K_{a^n}=^{m+n}C_n=\frac{(m+n)!}{m!n!}

As we can see K_{a^m}=K_{a^n} .

Hence it is proved that the coefficients of a^m and a^n are equal.

Question:10 The coefficients of the (r-1) th , r th and (r + 1) th terms in the expansion of (x+1)^{n} are in the ratio 1 : 3 : 5. Find n and r .

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So,

(r+1)^{th} Term in the expansion of (x+1)^{n} :

T_{r+1}=^nC_rx^{n-r}1^r=^nC_rx^{n-r}

r^{th} Term in the expansion of (x+1)^{n} :

T_{r}=^nC_{r-1}x^{n-r+1}1^{r-1}=^nC_{r-1}x^{n-r+1}

(r-1)^{th} Term in the expansion of (x+1)^{n} :

T_{r-1}=^nC_{r-2}x^{n-r+2}1^{r-2}=^nC_{r-2}x^{n-r+2}

Now, As given in the question,

T_{r-1}:T_r:T_{r+1}=1:3:5

^nC_{r-2}:^nC_{r-1}:^nC_{r}=1:3:5

\frac{n!}{(r-2)!(n-r+2)!}:\frac{n!}{(r-1)!(n-r+1)!}:\frac{n!}{r!(n-r)!}=1:3:5

From here, we get ,

\frac{r-1}{n-r+2}=\frac{1}{3}\:\:and\:\:\frac{r}{n-r+1}=\frac{3}{5}

Which can be written as

n-4r+5=0\:\:and\:\:3n-8r+3=0

From these equations we get,

n=7\:\:and\:\:r=3

Question:11 Prove that the coefficient of x^n in the expansion of (1+x)^{2n} is twice the coefficient of x^n in the expansion of (1+x)^{2n-1} .

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So, general (r+1)^{th} term T_{r+1} in the binomial expansion of (1+x)^{2n} is,

T_{r+1}=^{2n}C_r1^{2n-r}x^r

x^n will come when r=n ,

So, Coefficient of x^n in the binomial expansion of (1+x)^{2n} is,

K_{1x^n}=^{2n}C_n

Now,

the general (r+1)^{th} term T_{r+1} in the binomial expansion of (1+x)^{2n-1} is,

T_{r+1}=^{2n-1}C_r1^{2n-1-r}x^r

Here also x^n will come when r=n ,

So, Coefficient of x^n in the binomial expansion of (1+x)^{2n-1} is,

K_{2x^n}=^{2n-1}C_n

Now, As we can see

^{2n-1}C_n=\frac{(2n-1)!}{n!(2n-1-n)!}=\frac{(2n-1)!}{n!(n-1)!}=\frac{(2n)!}{2n(n!)(n-1)!}=\frac{(2n)!}{2(n!)(n!)}

^{2n-1}C_n=\frac{1}{2}\times^{2n}C_n

2\times^{2n-1}C_n=^{2n}C_n

2\times K_{2x^n}=K_{1x^n}

Hence, the coefficient of x^n in the expansion of (1+x)^{2n} is twice the coefficient of x^n in the expansion of (1+x)^{2n-1} .

Question:12 Find a positive value of m for which the coefficient of x^2 in the expansion (1 + x)^ m is 6.

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So, the general (r+1)^{th} term T_{r+1} in the binomial expansion of (1 + x)^ m is

T_{r+1}=^mC_r1^{m-r}x^r=^mC_rx^r

x^2 will come when r=2 . So,

The coeficient of x^2 in the binomial expansion of (1 + x)^ m = 6

\Rightarrow ^mC_2=6

\Rightarrow \frac{m!}{2!(m-2)!}=6

\Rightarrow \frac{m(m-1)}{2}=6

\Rightarrow m(m-1)=12

\Rightarrow m^2-m-12=0

\Rightarrow (m+3)(m-4)=0

\Rightarrow m=4\:or\:-3

Hence the positive value of m for which the coefficient of x^2 in the expansion (1 + x)^ m is 6, is 4.


Class 11 maths chapter 8 question answer - Miscellaneous Exercise

Question:1 Find a , b and n in the expansion of (a + b)^n if the first three terms of the expansion are 729, 7290 and 30375, respectively.

Answer:

As we know the Binomial expansion of (a + b)^n is given by

(a+b)^n=^nC_0a^n+^nC_1a^{n-1}b+^nC_2a^{n-2}b^2+......^nC_nb^n

Given in the question,

^nC_0a^n=729.......(1)

^nC_1a^{n-1}b=7290.......(2)

^nC_2a^{n-2}b^2=30375.......(3)

Now, dividing (1) by (2) we get,

\Rightarrow \frac{^nC_0a^n}{^nC_1a^{n-1}b}=\frac{729}{7290}

\Rightarrow \frac{\frac{n!}{n!0!}}{\frac{n!}{1!(n-1)!}}\times\frac{a}{b}=\frac{729}{7290}

\Rightarrow\frac{(n-1)!}{n!}\times\frac{a}{b}=\frac{1}{10}

\Rightarrow\frac{1}{n}\times\frac{a}{b}=\frac{1}{10}

10a=nb......(4)

Now, Dividing (2) by (3) we get,

\Rightarrow \frac{^nC_1a^{n-1}b}{^nC_2a^{n-2}b^2}=\frac{7290}{30375}

\Rightarrow \frac{\frac{n!}{1!(n-1)!}}{\frac{n!}{2!(n-2)!}}\times\frac{a}{b}=\frac{7290}{30375}

\Rightarrow \frac{2(n-2)!}{(n-1)!}\times\frac{a}{b}=\frac{7290}{30375}

\Rightarrow \frac{2}{(n-1)}\times\frac{a}{b}=\frac{7290}{30375}

\Rightarrow 2\times30375\times a=7290\times b\times(n-1)

\Rightarrow 60750a=7290b(n-1).......(5)

Now, From (4) and (5), we get,

n=6,a=3\:and\:b=5

Question:2 Find a if the coefficients of x^2 and x^3 in the expansion of (3 + ax)^9 are equal.

Answer:

As we know that the general (r+1)^{th} term T_{r+1} in the binomial expansion of (a+b)^n is given by

T_{r+1}=^nC_ra^{n-r}b^r

So, the general (r+1)^{th} term T_{r+1} in the binomial expansion of (3 + ax)^9 is

T_{r+1}=^nC_r3^{n-r}(ax)^r=^nC_r3^{n-r}a^rx^r

Now, x^2 will come when r=2 and x^3 will come when r=3

So, the coefficient of x^2 is

K_{x^2}=^nC_23^{9-2}a^2=^nC_23^7a^2

And the coefficient of x^3 is

K_{x^3}=^9C_33^{9-3}a^2=^9C_33^6a^3

Now, Given in the question,

K_{x^2}=K_{x^3}

^9C_23^7a^2=^9C_33^6a^3

\frac{9!}{2!7!}\times3=\frac{9!}{3!6!}\times a

a=\frac{18}{14}=\frac{9}{7}

Hence the value of a is 9/7.

Question:3 Find the coefficient of x^5 in the product (1 + 2x)^6 (1 - x)^7 using binomial theorem.

Answer:

First, lets expand both expressions individually,

So,

(1+2x)^6=^6C_0+^6C_1(2x)+^6C_2(2x)^2+^6C_3(2x)^3+^6C_4(2x)^4+^6C_5(2x)^5+ ^6C_6(2x)^6

(1+2x)^6=^6C_0+2\times^6C_1x+4\times^6C_2x^2+8\times^6C_3x^3+16\times^6C_4x^4+32\times^6C_5x^5+ 64\times^6C_6x^6

(1+2x)^6=1+12x+60x^2+160x^3+240x^4+192x^5+64x^6

And

(1-x)^7=^7C_0-^7C_1x+^7C_2x^2-^7C_3x^3+^7C_4x^4-^7C_5x^5+^7C_6x^6-^7C_7x^7

(1-x)^7=1-7x+21x^2-35x^3+35x^4-21x^5+7x^6-x^7

Now,

(1 + 2x)^6 (1 - x)^7=(1+12x+60x^2+160x^3+240x^4+192x^5+64x^6) (1-7x+21x^2-35x^3+35x^4-21x^5+7x^6-x^7)

Now, for the coefficient of x^5 , we multiply and add those terms whose product gives x^5 .So,

The term which contain x^5 are,

\Rightarrow (1)(-21x^5)+(12x)(35x^4)+(60x^2)(-35x^3)+(160x^3)(21x^2)+(240x^4)(-7x) +(192x^5)(1)

\Rightarrow 171x^5

Hence the coefficient of x^5 is 171.

Question:4 If a and b are distinct integers, prove that a - b is a factor of a^n - b^n , whenever n is a positive integer.
[ Hint: write a^n = (a - b + b)^n and expand]

Answer:

we need to prove,

a^n-b^n=k(a-b) where k is some natural number.

Now let's add and subtract b from a so that we can prove the above result,

a=a-b+b

a^n=(a-b+b)^n=[(a-b)+b]^n

=^nC_0(a-b)^n+^nC_1(a-b)^{n-1}b+........^nC_nb^n

=(a-b)^n+^nC_1(a-b)^{n-1}b+........^nC_{n-1}(a-b)b^{n-1}+b^n \Rightarrow a^n-b^n=(a-b)[(a-b)^{n-1}+^nC_2(a-b)^{n-2}+........+^nC_{n-1}b^{n-1}]

\Rightarrow a^n-b^n=k(a-b)

Hence, a - b is a factor of a^n - b^n .

Question:5 Evaluate \left(\sqrt3 + \sqrt2 \right )^6 - \left(\sqrt{3} - \sqrt2 \right )^6 .

Answer:

First let's simplify the expression (a+b)^6-(a-b)^6 using binomial theorem,

So,

(a+b)^6=^6C_0a^6+^6C_1a^5b+^6C_2a^4b^2+^6C_3a^3b^3+^6C_4a^2b^4+^6C_5ab^5+^6C_6b^6 (a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6

And

(a-b)^6=^6C_0a^6-^6C_1a^5b+^6C_2a^4b^2-^6C_3a^3b^3+^6C_4a^2b^4-^6C_5ab^5+^6C_6b^6

(a+b)^6=a^6-6a^5b+15a^4b^2-20a^3b^3+15a^2b^4-6ab^5+b^6

Now,

(a+b)^6-(a-b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6 -a^6+6a^5b-15a^4b^2+20a^3b^3-15a^2b^4+6ab^5-b^6

(a+b)^6-(a-b)^6=2[6a^5b+20a^3b^3+6ab^5]

Now, Putting a=\sqrt{3}\:and\:b=\sqrt{2}, we get

\left(\sqrt3 + \sqrt2 \right )^6 - \left(\sqrt{3} - \sqrt2 \right )^6=2[6(\sqrt{3})^5(\sqrt{2})+20(\sqrt{3})^3(\sqrt{2})^3+6(\sqrt{3})(\sqrt{2})^5]

\left(\sqrt3 + \sqrt2 \right )^6 - \left(\sqrt{3} - \sqrt2 \right )^6=2[54\sqrt{6}+120\sqrt{6}+24\sqrt{6}]

\left(\sqrt3 + \sqrt2 \right )^6 - \left(\sqrt{3} - \sqrt2 \right )^6=2\times198\sqrt{6}

\left(\sqrt3 + \sqrt2 \right )^6 - \left(\sqrt{3} - \sqrt2 \right )^6=396\sqrt{6}

Question:6 Find the value of \left(a^2 + \sqrt{a^2 -1} \right )^4 + \left(a^2 - \sqrt{a^2 -1} \right )^4

Answer:

First, lets simplify the expression (x+y)^4-(x-y)^4 using binomial expansion,

(x+y)^4=^4C_0x^4+^4C_1x^3y+^4C_2x^2y^2+^4C_3xy^3+^4C_4y^4

(x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4

And

(x-y)^4=^4C_0x^4-^4C_1x^3y+^4C_2x^2y^2-^4C_3xy^3+^4C_4y^4

(x-y)^4=x^4-4x^3y+6x^2y^2-4xy^3+y^4

Now,

(x+y)^4-(x-y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4- x^4+4x^3y-6x^2y^2+4xy^3-y^4

(x+y)^4-(x-y)^4=2(x^4+6x^2y^2+y^4)

Now, Putting x=a^2\and\:y=\sqrt{a^2-1} we get,

\left(a^2 + \sqrt{a^2 -1} \right )^4 + \left(a^2 - \sqrt{a^2 -1} \right )^4=2[(a^2)^4+6(a^2)^2(\sqrt{a^2-1})^2+(\sqrt{a^2-1})^4]

\left(a^2 + \sqrt{a^2 -1} \right )^4 + \left(a^2 - \sqrt{a^2 -1} \right )^4=2[a^8+6a^4(a^2-1)+(a^2-1)^2]

\left(a^2 + \sqrt{a^2 -1} \right )^4 + \left(a^2 - \sqrt{a^2 -1} \right )^4=2a^8+12a^6-12a^4+2a^4-4a^2+2

\left(a^2 + \sqrt{a^2 -1} \right )^4 + \left(a^2 - \sqrt{a^2 -1} \right )^4=2a^8+12a^6-10a^4-4a^2+2

Question:7 Find an approximation of (0.99) 5 using the first three terms of its expansion.

Answer:

As we can write 0.99 as 1-0.01,

(0.99)^5=(1-0.001)^5=^5C_0(1)^5-^5C_1(1)^4(0.01)+^5C_2(1)^3(0.01)^2 +\:other \:negligible \:terms

\Rightarrow (0.99)^5=1-5(0.01)+10(0.01)^2

\Rightarrow (0.99)^5=1-0.05+0.001

\Rightarrow (0.99)^5=0.951

Hence the value of (0.99)^5 is 0.951 approximately.

Question:8 Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of \left(\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}} \right )^n is \sqrt6 :1

Answer:

Given, the expression

\left(\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}} \right )^n

Fifth term from the beginning is

T_5=^nC_4(\sqrt[4]{2})^{n-4}\left(\frac{1}{\sqrt[4]{3}}\right)^4

T_5=^nC_4\frac{(\sqrt[4]{2})^n}{(\sqrt[4]{2})^4}\times\frac{1}{3}

T_5=\frac{n!}{4!(n-4)!}\times\frac{(\sqrt[4]{2})^n}{2}\times\frac{1}{3}

And Fifth term from the end is,

T_{n-5}=^nC_{n-4}(\sqrt[4]{2})^4\left ( \frac{1}{\sqrt[4]{3}} \right )^{n-4}

T_{n-5}=^nC_{n-4}(\sqrt[4]{2})^4\left ( \frac{(\sqrt[4]{3})^4}{(\sqrt[4]{3})^n} \right )

T_{n-5}=\frac{n!}{4!(n-4)!}\times2\times\left ( \frac{3}{(\sqrt[4]{3})^n} \right )

Now, As given in the question,

T_5:T_{n-5}=\sqrt{6}:1

So,

\left(\frac{n!}{4!(n-4)!}\times\frac{(\sqrt[4]{2})^n}{2}\times\frac{1}{3}\right):\left( \frac{n!}{4!(n-4)!}\times2\times\left ( \frac{3}{(\sqrt[4]{3})^n} \right )\right)=\sqrt{6}:1

From Here ,

\frac{(\sqrt[4]{2})^n}{6}:\frac{6}{(\sqrt[4]{3})^n}=\sqrt{6}:1

\frac{(\sqrt[4]{2})^n(\sqrt[4]{3})^n}{6\times6}=\sqrt{6}

(\sqrt[4]{6})^n=36\sqrt{6}

6^{\frac{n}{4}}=6^{\frac{5}{2}}

From here,

\frac{n}{4}=\frac{5}{2}

n=10

Hence the value of n is 10.

Question:9 Expand using Binomial Theorem \left(1 + \frac{x}{2} - \frac{2}{x} \right )^4, \ x\neq 0

Answer:

Given the expression,

\left(1 + \frac{x}{2} - \frac{2}{x} \right )^4, \ x\neq 0

Binomial expansion of this expression is

\\\left(1 + \frac{x}{2} - \frac{2}{x} \right )^4\\=\left ( \left (1 + \frac{x}{2} \right ) -\frac{2}{x}\right )^4=^4C_0\left ( 1+\frac{x}{2} \right )^4-^4C_1\left ( 1+\frac{x}{2} \right )^3\left ( \frac{2}{x} \right )+ ^4C_2\left ( 1+\frac{x}{2} \right )^2\left ( \frac{2}{x} \right )^2 -^4C_3\left ( 1+\frac{x}{2} \right )\left ( \frac{2}{x} \right )^3+^4C_4\left ( \frac{2}{x} \right )^4

\Rightarrow \left ( 1+\frac{x}{2} \right )^4-\frac{8}{x}\left ( 1+\frac{x}{2} \right )^3+ \frac{24}{x^2}+\frac{24}{x}+6 -\frac{32}{x^3}+\frac{16}{x^4}..........(1)

Now Applying Binomial Theorem again,

\left ( 1+\frac{x}{2} \right )^4=^4C_0(1)^4+^4C_1(1)^3\left ( \frac{x}{2} \right )+^4C_2(1)^2\left ( \frac{x}{2} \right )^2+^4C_3(1)\left ( \frac{x}{2} \right )^3 +^4C_4\left ( \frac{x}{2} \right )^4

= 1+ 4\left ( \frac{x}{2} \right )+6\left ( \frac{x^2}{4} \right )+4\left ( \frac{x^3}{8} \right )+\frac{x^4}{16}

=1+2x+\frac{3x^2}{2}+\frac{x^3}{3}+\frac{x^4}{16}..............(2)

And

\left ( 1+\frac{x}{2} \right )^3=^3C_0(1)^3+^3C_1(1)^2\left ( \frac{x}{2} \right )+^3C_2(1)\left ( \frac{x}{2} \right )^2+^3C_3\left ( \frac{x}{2} \right )^3

\left ( 1+\frac{x}{2} \right )^3= 1+\frac{3x}{2}+\frac{3x^2}{4}+\frac{x^3}{8}..........(3)

Now, From (1), (2) and (3) we get,

\\\left(1 + \frac{x}{2} - \frac{2}{x} \right )^4=1+2x+\frac{3x^2}{2}+\frac{x^3}{8}+\frac{x^4}{16}-\frac{8}{x}\left ( 1+\frac{3x}{2}+\frac{3x^2}{4}+\frac{x^2}{8} \right ) +\frac{8}{x^2}+\frac{24}{x}+6-\frac{32}{x^3}+\frac{16}{x^4}

\\\left(1 + \frac{x}{2} - \frac{2}{x} \right )^4=1+2x+\frac{3x^2}{2}+\frac{x^3}{8}+\frac{x^4}{16}-\frac{8}{x}-12-6x-x^2 +\frac{8}{x^2}+\frac{24}{x}+6-\frac{32}{x^3}+\frac{16}{x^4}

\\\left(1 + \frac{x}{2} - \frac{2}{x} \right )^4=1+2x+\frac{3x^2}{2}+\frac{x^3}{8}+\frac{x^4}{16}-\frac{8}{x}\left ( 1+\frac{3x}{2}+\frac{3x^2}{4}+\frac{x^2}{8} \right ) =\frac{16}{x}+\frac{8}{x^2}-\frac{32}{x^3}+\frac{16}{x^4}-4x+\frac{x^2}{2}+\frac{x^3}{2}+\frac{x^4}{16}-5

Question:10 Find the expansion of (3x^2 - 2ax +3a^2)^3 using binomial theorem .

Answer:

Given (3x^2 - 2ax +3a^2)^3

By Binomial Theorem It can also be written as

(3x^2 - 2ax +3a^2)^3=((3x^2 - 2ax) +3a^2)^3

= ^3C_0(3x^2-2ax)^3+^3C_1(3x^2-2ax)^2(3a^2)+^3C_2(3x^2-2ax)(3a^2)^2+^3C_3(3a^2)^3

= (3x^2-2ax)^3+3(3x^2-2ax)^2(3a^2)+3(3x^2-2ax)(3a^2)^2+(3a^2)^3

= (3x^2-2ax)^3+81a^2x^4-108a^3x^3+36a^4x^2+81a^4x^2-54a^5x+27a^6

= (3x^2-2ax)^3+81a^2x^4-108a^3x^3+117a^4x^2-54a^5x+27a^6...........(1)

Now, Again By Binomial Theorem,

(3x^2-2ax)^3=^3C_0(3x^2)^3-^3C_1(3x^2)^2(2ax)+^3C_2(3x^2)(2ax)^2-^3C_3(2ax)^3

(3x^2-2ax)^3= 27x^6-3(9x^4)(2ax)+3(3x^2)(4a^2x^2)-8a^2x^3

(3x^2-2ax)^3= 27x^6-54x^5+36a^2x^4-8a^3x^3............(2)

From (1) and (2) we get,

(3x^2-2ax+3a^2)^3=27x^6-54x^5+36a^2x^3+81a^2x^4-108a^3x^3+117a^4x^2 -54a^5x+27a^6

(3x^2-2ax+3a^2)^3=27x^6-54x^5+117a^2x^3-116a^3x^3+117a^4x^2 -54a^5x+27a^6

Highlights of NCERT Solutions for Class 11 Maths Chapter 8 – Binomial Theorem

8.1 Introduction

8.2 Binomial Theorem for Positive Integral Indices

  • Pascal’s Triangle
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

8.2.1 Binomial theorem for any positive integer n

8.2.2 Some special cases

8.3 General and Middle Term

If you are interested in Binomial Theorem class 11 exercise solutions then these are listed below.

Binomial Theorem class 11 exercise 8.1

Binomial Theorem class 11 exercise 8.2

Binomial Theorem class 11 exercise miscellaneous exercise

NCERT solutions for class 11 mathematics

chapter-1Sets
chapter-2Relations and Functions
chapter-3Trigonometric Functions
chapter-4Principle of Mathematical Induction
chapter-5Complex Numbers and Quadratic equations
chapter-6Linear Inequalities
chapter-7Permutation and Combinations
chapter-8Binomial Theorem
chapter-9Sequences and Series
chapter-10Straight Lines
chapter-11Conic Section
chapter-12Introduction to Three Dimensional Geometry
chapter-13Limits and Derivatives
chapter-14Mathematical Reasoning
chapter-15Statistics
chapter-16Probability

Key Features of NCERT Solutions for Class 11 Maths Chapter 8 – Binomial Theorem

Comprehensive explanations: The solutions of maths chapter 8 class 11 provide step-by-step explanations to all the questions in the chapter, helping students to understand the concepts thoroughly.

NCERT-based: The solutions of ch 8 maths class 11 are strictly based on the latest NCERT syllabus and follow the guidelines set by the board.

Easy language: The class 11 maths ch 8 question answer are written in simple and easy-to-understand language, making it easy for students to grasp the concepts.

NCERT solutions for class 11- Subject wise

NCERT solutions for class 11 biology
NCERT solutions for class 11 maths
NCERT solutions for class 11 chemistry
NCERT solutions for Class 11 physics

Important Formulas

The binomial theorem for a positive integer n

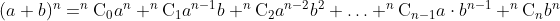
(a+b)^{n}=^{n} \mathrm{C}_{0} a^{n}+^{n} \mathrm{C}_{1} a^{n-1} b+^{n} \mathrm{C}_{2} a^{n-2} b^{2}+\ldots+^{n} \mathrm{C}_{n-1} a \cdot b^{n-1}+^{n} \mathrm{C}_{n} b^{n}

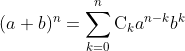
(a+b)^{n}=\sum_{k=0}^{n} \mathrm{C}_{k} a^{n-k} b^{k}

^{n} \mathrm{C}_{r} -> binomial coefficients.

Some special cases

Put a=1, b=x (1+x)^{n}=^{n} C_{0}+^{n} C_{1} x+^{n} C_{z} x^{2}+^{n} C_{3} x^{3}+\ldots+^{n} C_{n} x^{n}

Put x=1 2^{n}=^{n} \mathrm{C}_{0}+^{n} \mathrm{C}_{1}+^{n} \mathrm{C}_{2}+\ldots+^{n} \mathrm{C}_{n}

Put a=1,b=-x (1-x)^{n}=^{n} \mathrm{C}_{0}-^{n} \mathrm{C}_{1} x+^{n} \mathrm{C}_{2} x^{2}-\ldots+(-1)^{n} \mathrm{C}_{n} x^{n}

Put x=1 0=^{n} \mathrm{C}_{0}-^{n} \mathrm{C}_{1}+^{n} \mathrm{C}_{2}-\ldots+(-1)^{n} \mathrm{C}_{n}

There are 10 problems with miscellaneous exercise. To get command on this chapter, you need to solve miscellaneous exercises too. In NCERT solutions for class 11 maths chapter 8 binomial theorem, you will get solutions to miscellaneous exercises too.

Also Check NCERT Books and NCERT Syllabus here

Happy Reading !!!

Frequently Asked Question (FAQs)

1. What are important topics of the chapter Chapter 8 Binomial Theorem ?

The basic concept of the binomial theorem, binomial theorem for positive integral indices, and general and middle terms are covered in this chapter. students can go through the NCERT syllabus, all the important topics are mentioned there. practicing these topics covered in binomial theorem ncert solutions is crucial for commanding the concepts. 

2. How does the NCERT solutions are helpful ?

NCERT solutions are helpful to the students while solving the NCERT problems. After solving NCERT book problems students can acquire command in concepts that will help greatly during premier exams. If they are stuck while solving, they can take help with binomial theorem class 11 NCERT solutions provided in a detailed manner.  for ease students can study class 11 maths chapter 8 solutions pdf both online and offline mode.

3. Explain the concept of the Binomial Theorem covered in NCERT solutions for class 11th maths chapter 8.

The Binomial Theorem refers to the method of expanding the power of binomials that involve the addition of two or more terms. The coefficients of the terms in the expansion are known as binomial coefficients. This chapter provides essential definitions that are relevant for examinations. With the NCERT Solutions available in PDF format, students can stay up-to-date with the latest CBSE Board syllabus.

4. Where can I find the complete solutions of NCERT for class 11 maths ?

Here you will get the detailed NCERT solutions for class 11 maths by clicking on the link. if anyone facing problems to find complete solutions of NCERT Book can web through official website of Careers360 or these are listed above in the article according to topic and subject wise.

5. In the Binomial Theorem, explain the properties of positive integers covered in the class 11 maths NCERT solutions chapter 8.

The NCERT Solutions for Class 11 Maths Chapter 8 provide over 10 properties related to positive integers that students can learn. These properties are crucial in comprehending the efficient solution of equations. During the annual examination, the question paper may focus on simple chapters that are challenging to solve. Hence, it is recommended that students go through these NCERT Solutions to secure good marks in the examination.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Madhya Pradesh Board 10th Examination

Application Date:01 May,2024 - 20 May,2024

Madhya Pradesh Board 12th Examination

Application Date:01 May,2024 - 20 May,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

ALLEN NEET Coaching
ALLEN NEET Coaching
Apply

Ace your NEET preparation with ALLEN Online Programs

View All Application Forms
News and Notifications
Barmer teacher suspended for slapping class 3 student
01/05/2024, 17:07:10
Teacher arrested for `sexual exploitation' at Ujjain Ashram school
01/05/2024, 14:28:18
Delhi NCR schools get bomb threat; fire tender arrives, search underway
01/05/2024, 04:09:04
Education is greatest gift to society: Vice President Jagdeep Dhankhar
30/04/2024, 17:02:12
Jharkhand schools up to Class 8 closed till further orders due to heat wave
30/04/2024, 11:49:37
Delhi School EWS Admission 2024-25: Registration window opens at edudel.nic.in; eligibility
30/04/2024, 09:27:25
Education ministry asks NCERT to review, update textbooks on yearly basis
29/04/2024, 12:22:03
Back to top