The Pythagoras theorem also known as the Pythagorean theorem is an interesting fundamental relationship among the three sides of a right-angle triangle. In mathematics, this is a part of Euclidean geometry. This article comprehensively explains the real life applications of Pythagoras Theorem. Let's begin by understanding the theorem first.

Pythagoras Theorem

An ancient Indian mathematician Baudhayan (about 800 B.C.E) described a relation that in a rectangle area produced by his length and breath is equal to the area produced by the diagonal. For this reason, this is sometimes known as the Baudhayan theorem But the credit for the same relation goes to Pythagoras.

Pythagoras (570 B.C.E to 495 B.C.E) was a Greek mathematician, philosopher, and politician whose immense contributions to mathematics. One of the most important contributions is Pythagoras theorem.

The theorem states that in a right-angle triangle, the sum of the square of two sides connected to the right angle is equal to the sum of the square of the third side which is known as the hypotenuse.

(Height)² + (Base)² = (Hypotenuse)²

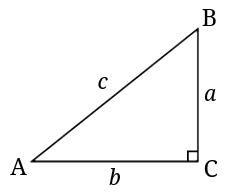
Here in this triangle ABC, angle C is 90 degrees or right angle, and sides AC, and BC are connected to right angle C respectively called Base and Height corresponding to angle A. Side AB is called the hypotenuse.

According to Pythagoras theorem

(BC)² + (AC)² = (AB)²

(a)² + (b)² = (c)²

Pythagoras theorem is critically used in NCERT Class 10 chapter 6, Triangles. It helps in proofing the similarity of triangles, other theorems, and calculating different sides of a right-angle triangle.

The theorem is used in different Chapters of NCERT Class 9. Particularly In Chapter 9, the theorem is used in calculating the area of parallelograms and triangles. In Chapter 13, this theorem helps in calculating the surface area and volume of different shapes.

Now let's discuss some real life applications of Pythagoras theorem.

Also Read| JEE Main, NEET 2022: How To Tackle Class 12 Inorganic Chemistry

Consequences Of Pythagoras Theorem

Following are some uses of Pythagoras theorem in deriving other concepts of mathematics.

Pythagorean Triples

A combination of three positive integers a, b, and c, such that a² + b² = c² is known as Pythagoras triplets. The triple can also represent the three sides of a rectangle triangle. Triples are generally written as (a, b, c). There are some triples: (3,4,5), (5,12,13), (7,24,25), (8,15,17)...etc.

Incommensurable Lengths

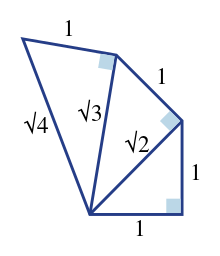
One of the important consequences of Pythagoras theorem is constructing a line segment using a straightedge and compass whose length is incommensurable. In other words, the length is an irrational number or can not be in the form of a/b where a and b are two integers. Pythagoras theorem says that in a right-angle triangle hypotenuse is a square root of the square of the other two sides and thus it enables the construction of incommensurable lengths like √2, √3, √5,.. The following image shows very clearly.

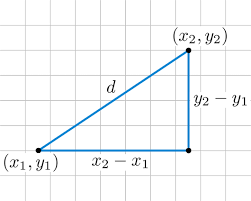
Euclidean Distance

In the cartesian coordinate system distance between two points can be calculated using The distance formula which is derived from the Pythagorean theorem. The distance (d) is the square root of the sum of squares of the x-component (x₂-x₁) and the square of the y-component (y₂-y₁) which is known as Euclidean distance is shown in the following image.

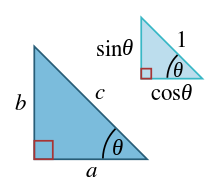
Trigonometric Identity

a, b, and hypotenuse c, are sides of a right-angle triangle. If the angle θ between hypotenuse and side then trigonometric ratios like sine, cosine, and tan. can be determined as respectively b/c, a/c, and b/a. For unit hypotenuse, the Pythagoras theorem can be written for a given triangle as

(sinθ)² + (cosθ)²= 1

This identity is known as Pythagorean trigonometric identity

Real Life Applications Of Pythagoras Theorem

The theorem has vast applications in real life. Let's discuss some real life uses of Pythagoras theorem.

Shortest Distance

The Pythagorean Theorem is useful to find the shortest distances in two-dimensional navigation. If a person goes East for x distance and then turns North and moves for y distance. The shortest distance between the initial and final stages can be calculated by Pythagoras theorem because the East and North distance can be considered as legs of a right-angle triangle. The diagonal shows the shortest distance. The same principle can be used for air, water, navigation, etc.

Pythagoras Theorem In A Security Camera

Nowadays face recognition becomes very important in security areas and it reduces the turmoil in an investigation of a crime. The concept of a Pythagoras theorem is helpful to calculate the distance between the position of the camera and the place where the crime is noted and it is also helpful to set the angle for face recognition in security cameras.

Surveying The Mountains

Usually, a mountain surveyor finds the steepness of a mountain or hill. After knowing the horizontal distance, It becomes easy to find other measurements using the application of Pythagoras theorem. We can fix the horizontal distance between the telescope and the mountain. Using the telescope, the steepness of mountains can be measured.

Engineering And Construction Fields

This Theorem is very useful in measurements of construction mainly in two dimensions. Most architects apply these techniques to calculate values like their height, length, etc., and if these are known it becomes easy to find out the other parameters like the diameter of a particular sector.

Wall Painting

The Painters often use Pythagoras theorem. Ladders are required to paint the high building. Painters need to determine the suitable height of the ladder in order to safely place it away from the wall.

Television Or Monitor Size

TV and Monitor sizes are always given in terms of diagonal size. Pythagoras theorem can be used to find the lengths of sides of a rectangle shaped monitor or television.

Original Height Of A Broken Tree

A broken tree can form a right-angle triangle and using the application of Pythagoras theorem the original height of the tree can be calculated.

There is a vast application of Pythagoras theorem in real life, some of which are discussed in this article. Therefore understanding the Pythagoras theorem becomes very important for students.