RD Sharma Class 12 Exercise 22.4 Algebra of Vectors Solutions Maths

RD Sharma Class 12 Exercise 22.4 Algebra of Vectors Solutions Maths - Download PDF Free Online

Updated on Jan 24, 2022 06:19 PM IST

One of the most important and interesting chapters in Class 12 Mathematics is vector algebra. We will look at the algebra of vector quantities and how they differ from scalar quantities. Physical quantities are classified into two types: scalars and vectors. A scalar quantity has magnitude only, whereas a vector has magnitude and direction as well. For each chapter, RD Sharma solutions provide exercise-by-exercise solutions. RD Sharma Class 12th Exercise 22.4 includes 6 questions and examples to make the journey easier for all students. This particular exercise, which would be useful for an exam, discusses position vectors, components of a vector in two dimensions.

This Story also Contains

RD Sharma Class 12 Solutions Chapter22 Algebra of vectors - Other Exercise
Algebra of Vectors Excercise: 22.4
Algebra of vector exercise 22.4 question 4
RD Sharma Chapter wise Solutions

RD Sharma Class 12 Solutions Chapter22 Algebra of vectors - Other Exercise

Algebra of Vectors Excercise: 22.4

Algebra of vector exercise 22.4 question 2

Answer:

Hence it has been proved that the sum of median vectors is zero.
Hint:
With the help of vector algebra.
Given:
A, B and C are the three vertices of the triangle and D,E,F are the mid points of the line BD, CA and AB respectively.
Solution :
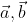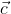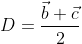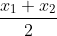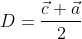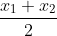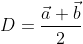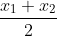Let ABC is a triangle such that p.v of A,B,C are $\vec{a},\vec{b}$ and $\vec{c}$ and c respectively.As AD,BE and CF are medians ,D,E,F are midpoints.P.V of $D=\frac{\vec{b}+\vec{c}}{2}$ [ Using midpoint formula $\frac{x_{1}+x_{2}}{2}$ ]P.V of $D=\frac{\vec{c}+\vec{a}}{2}$ [ Using midpoint formula $\frac{x_{1}+x_{2}}{2}$ ]P.V of $D=\frac{\vec{a}+\vec{b}}{2}$ [ Using midpoint formula $\frac{x_{1}+x_{2}}{2}$ ]Now, $\begin{aligned} &\overrightarrow{A D}+\overrightarrow{B E}+\overrightarrow{C F} \\ \end{aligned}$ $\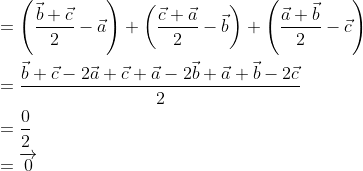begin{aligned} &=\left(\frac{\vec{b}+\vec{c}}{2} -\vec{a}\right)+\left(\frac{\vec{c}+\vec{a}}{2} -\vec{b}\right)+\left(\frac{\vec{a}+\vec{b}}{2} - \vec{c}\right) \\ &=\frac{\vec{b}+\vec{c}-2 \vec{a}+\vec{c}+\vec{a}-2 \vec{b}+\vec{a}+\vec{b}-2 \vec{c}}{2} \\ &=\frac{0}{2} \\ &=\overrightarrow{0}\end{aligned}$

Algebra of vector exercise 22.4 question 3

Answer:

$\vec{OA}+\vec{OB}+\vec{OC}+\vec{OD}=4\vec{OP}$.....hence proved
Hint:
With the help of vector algebra.
Given:
A,B,C and D are the vertices of the quadrilateral.
Solution :
Using the triangle law in ?AOP
$\vec{OP}+\vec{PA}=\vec{OA}$ ?(i)
Using the triangle law in ?ABP
$\vec{OP}+\vec{PB}=\vec{OB}$ ?(ii)
Using the triangle law in ?OPC
$\vec{OP}+\vec{PC}=\vec{OC}$ ?(iii)
Using the triangle law in ?OPD
$\vec{OP}+\vec{PD}=\vec{OD}$ ?(iv)
Adding all the equations,
$\begin{aligned} &\overrightarrow{O P}+\overrightarrow{P A}+\overrightarrow{O P}+\overrightarrow{P B}+\overrightarrow{O P}+\overrightarrow{P C}+\overrightarrow{O P}+\overrightarrow{P D}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O D}+\overrightarrow{O C} \\ &\overrightarrow{P A}+\overrightarrow{P B}+\overrightarrow{P C}+\overrightarrow{P D}+4 \overrightarrow{O P}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O D}+\overrightarrow{O C} \\ &4 \overrightarrow{O P}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O D}+\overrightarrow{O C} \ldots a s \overrightarrow{P A}=-\overrightarrow{P C} \& \overrightarrow{P B}=-\overrightarrow{P D} \end{aligned}$

…hence proved

Algebra of vector exercise 22.4 question 4

Answer:

Hence, line segments joining the midpoints of opposite sides of a quadrilateral bisects each other.
Hint:
With the help of vector algebra.
Given:
We have line segments joining the midpoints of opposite sides of a quadrilateral
Solution :
Let the quadrilateral be an parallelogram so the line segments joining the midpoints of opposite sides of the quadrilateral becomes its diagonals
Let A be the origin and $AB=\vec{a}$ and $AD=\vec{b}$

As the diagonals of an parallelogram bisect each other so the line segments joining the midpoints of opposite sides of a quadrilateral bisects each other as the line segments becomes parallel to the diagonals of the quadrilateral.

Algebra of vector exercise 22 point 4 question 5

Answer:

We need to prove that,
$\vec{PA}+\vec{PB}+\vec{PC}+\vec{PD}=4 \vec{PQ}$
Hint:
With the help of vector algebra.
Given:
We have given plane ABCD, where Q is point of intersection of the line joining the midpoints of AB and CD; BC and AD.
Solution :
Let $\vec{a},\vec{b},\vec{c},\vec{d}$ be the P.V of the point A,B,C,D respectively.
midpoint of $AB=\frac{\vec{a}+\vec{b}}{2}$
midpoint of $BC=\frac{\vec{b}+\vec{c}}{2}$
midpoint of $CD=\frac{\vec{c}+\vec{d}}{2}$
midpoint of $DA=\frac{\vec{d}+\vec{a}}{2}$
is the midpoint joining the midpoint of AB and CD
Let P be the P.V of P
P.V of Q=$\frac{\frac{a-b}{2}+\frac{c+d}{2}}{2}$ [ Using midpoint formula $\frac{x_{1}+x_{2}}{2}$]
$=\frac{a+b+c+d}{4}$
Let P be the P.V of p
$\begin{aligned} &P A+P B+P C+P D=\frac{1}{2}[\vec{a}-\vec{p}+\vec{b}-\vec{p}+\vec{c}-\vec{p}+\vec{d}-\vec{p}] \\ &=(\vec{a}+\vec{b}+\vec{c}+\vec{d})-4 \vec{p} \\ &=4\left(\frac{\vec{a}+\vec{b}+\vec{c}+\vec{d}}{4}-p\right) \\ &=4(\overrightarrow{O Q}-\overrightarrow{O P}) \\ &=4 \overrightarrow{P Q} \end{aligned}$.......hence Proved

Algebra of vector exercise 22.4 question 6

Answer:

The internal bisectors of the angles of a triangle are concurrent.
Hint:
With the help of vector algebra.
Given:
Concurrent bisector denotes the quality of internal bisectors.

Let ABC be the triangle and $\vec{\alpha},\vec{\beta },\vec{\gamma }$ be the position vectors of the vertices A,B and C respectively. Let AD,BE and CF be the internal bisectors of $\angle A,\angle B$ and$\angle C$ respectively.
We know that D divides BC in the ratio of AB:AC that is c:b.
Then,
Postiton vector of D is $\frac{c\vec{\gamma }+b\vec{\beta }}{c+b}$
Position vector of E is $\frac{c\vec{\gamma }+b\vec{\beta }}{c+b}$ and of F is $\frac{a\vec{\alpha }+b\vec{\beta }}{a+b}$
The point dividing AD in the ratio b+c : a is $\frac{a\vec{\alpha }+b\vec{\beta }+c\vec{\gamma }}{a+b+c}$
The point dividing BE in the ratio a+c : b is $\frac{a\vec{\alpha }+b\vec{\beta }+c\vec{\gamma }}{a+b+c}$
The point dividing CF in the ratio a+b : c is $\frac{a\vec{\alpha }+b\vec{\beta }+c\vec{\gamma }}{a+b+c}$
Since the point $\frac{a\vec{\alpha }+b\vec{\beta }+c\vec{\gamma }}{a+b+c}$ lies on all the three internal bisectors AD,BE and CF .Hence the internal bisectors are concurrent.

Class 12th RD Sharma Chapter 22 Exercise 22.4 Solutions are prepared by a team of experts using the most recent NCERT textbook and latest CBSE guidelines. The concepts related to vectors in two dimensions are detailed very well and when a student refers to RD Sharma Class 12 Solutions Algebra of Vectors Ex. 22.4, a high score is a sure outcome. The following advantages will accrue to a student who refers to RD Sharma Class 12 Solutions Chapter 22 ex 22.4:

1. Especially designed for all students:

RD Sharma Class 12 Solutions Chapter 22 ex 22.4 are created by subject matter experts by the most recent marking pattern and CBSE guidelines. RD Sharma Class 12th Exercise 22.4 must be referred to by all the students to score well academically. These solutions explain the above-mentioned topics in such a way that even a newcomer can learn and solve them.

2. The most effective source of preparation for JEE and Board exams:

RD Sharma Class 12th Exercise 22.4 solutions are a great source because of their high quality format. It is an excellent choice because of the most recent NCERT and CBSE updates. Our experts are familiar with the marking scheme and they provide solutions that will help students get good grades.

3. Questions from the NCERT textbooks:

The NCERT is typically used to set exam questions and widely used all over India. Teachers set question papers from NCERT textbooks, so it is necessary to learn NCERT concepts and answer questions.

4. Answering a question in various ways:

When a team develops a solution, each expert has a unique approach to solving the question. As a result, the experts have found different approaches to answer a single question, which distinguishes us.

5. Great performance for students:

Students benefit a lot from these solutions because of the level of simplicity in language. RD Sharma Class 12 Solutions Ex. 22.4 covers all the essential exam questions, allowing students to establish a benchmark score.

6. The solutions are free of cost:

RD Sharma solutions are available to all students at zero cost at Career360, the great website where a student will find all the questions related to board exam questions and competitive exams. A student will understand, learn, and perform exceptionally well in exams with Career360. Thousands of students have already availed the benefits of Careers360, a student must not lag behind from getting the benefits.

RD Sharma Chapter wise Solutions

Frequently Asked Questions (FAQs)

1. What is the difference between a scalar quantity and a vector quantity?

A scalar quantity has only magnitude (size or measurement), whereas a vector quantity has magnitude as well as direction. Speed, for example, is a scalar quantity, whereas velocity is a vector quantity.

2. Which website is the best for RD Sharma Solutions?

The RD Sharma Solutions offered by Career360 have been created by top subject experts in the country. It offers solutions in the chapter- and exercise-based formats for ease of use. Furthermore, students can view RD Sharma Solutions online or download them for offline viewing, making Career360's RD Sharma Solutions the best among the rest.

3. Where can I find RD Sharma Solutions for Class 12 Maths Chapter 22 exercise-by-exercise answers?

Students in Class 12 should select appropriate study materials to help them solve textbook problems efficiently. In Career360, the solutions to both chapter and exercise problems are available. It can be referred to by students while solving problems to quickly clear their doubts.

4. What are the Vector Addition Laws?

The two main vector addition laws are as follows:

A + B = B + A is a commutative law.

A + (B + C) = (A + B) + C is an Associative Law.

5. What are the concepts that are discussed in RD Sharma Algebra of vectors Class 12th solutions?

The central concepts that are discussed are as follows: