RD Sharma Class 12 Exercise 22.2 Algebra of Vectors Solutions Maths

RD Sharma Class 12 Exercise 22.2 Algebra of Vectors Solutions Maths - Download PDF Free Online

Edited By Satyajeet Kumar | Updated on Jan 24, 2022 06:19 PM IST

The study of vectors and scalars is the focus of Vector Algebra for Class 12. Several quantities involve both magnitude and direction. Vectors are quantities that have magnitude as well as direction. Vector Quantities are the names given to such quantities—displacement, velocity, force, weight, acceleration, momentum, electric intensity, and so on. RD Sharma solutions When a student is facing difficulty, RD Sharma Class 12th Exercise 22.2 comes to help them.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics

This Story also Contains

RD Sharma Class 12 Solutions Chapter22 Algebra of vectors - Other Exercise
Algebra of Vectors Excercise: 22.2
Algebra of Vectors Exercise 22.2 Question 9
RD Sharma Chapter wise Solutions

RD Sharma Class 12th Chapter 22 Exercise 22.2 has exercise-wise questions in this book. This particular exercise has 10 questions from the chapter 'Algebra of Vectors.' The concepts discussed in this exercise are Collinear and Non-Collinear Points, truth values, how to solve vectors, Proving like ABCD is a IIgm, and many more. Practicing these questions is vital for every student.

RD Sharma Class 12 Solutions Chapter22 Algebra of vectors - Other Exercise

Algebra of Vectors Excercise: 22.2

Algebra of Vectors Exercise 22.2 Question 1

Answer:
The value of $\vec{PR}=\vec{a}+\vec{b}$
Hint:
Use, $\vec{PQ}+\vec{QR}=\vec{PR}$
Given:
P,Q,R are collinear.
Solution:
95789

P,Q,R are collinear, they lie on the same line
$\begin{aligned} &\overrightarrow{P Q}=\vec{a} \text { and } \overrightarrow{P R}=\vec{b} \\ &\overrightarrow{P Q}+\overrightarrow{Q R}=\overrightarrow{P R} \\ &\vec{a}+\vec{b}=\overrightarrow{P R} \\ &\overrightarrow{P R}=\vec{a}+\vec{b} \end{aligned}$

Algebra of Vectors Exercise 22.2 Question 2

Answer:
The possiblilities are
(i) $\vec{a}+\vec{b}+\vec{c}=0$
(ii) $\vec{a}=\vec{b}+\vec{c}$
(iii) $\vec{c}=\vec{a}+\vec{b}$
(iv) $\vec{b}=\vec{a}+\vec{c}$
Hint:
Use triangle law of addition.
Given:
$\vec{a},\vec{b},\vec{c}$ are three sides of the triangle
Solution: tri

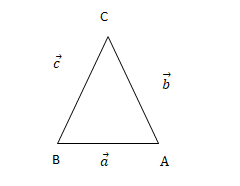$\begin{aligned} &\overrightarrow{A B}=\vec{a} \\ &\overrightarrow{B C}=\vec{b} \\ &\therefore \overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C} \\ &\vec{a}+\vec{b}=-\vec{c} \\ &\vec{a}+\vec{b}+\vec{c}=0 \\ \end{aligned}$

The other possibilities are
$\begin{aligned} &\vec{a}=\vec{b}+\vec{c} \\ &\vec{c}=\vec{a}+\vec{b} \\ &\vec{b}=\vec{a}+\vec{c} \end{aligned}$

Algebra of Vectors Exercise 22.2 Question 3

Answer:

$\vec{a}+\vec{b}$ and $\vec{d}-\vec{b}$ are the diagonals of parallelogram. whose adjacent sides are $\vec{a}$ and $\vec{b}$
Hint:
Use triangle law of vector.
Given :
$\vec{a},\vec{b},\vec{c}$ are three sides of triangle
Solution:
$\vec{a}$ and $\vec{b}$ are two collinear vectors having the same initial point.
Let $AB= \vec{a}$ and $AD= \vec{b}$
let us draw a parallelogram with AB and AD as any of two sides of the parallelogram.
We know in parallelogram opposite sides are equal hence,
$DC= \vec{a}$ and $BC= \vec{b}$
Now consider $\Delta ABC$ , applying
Triangle law of vector we got,
95792
$\begin{aligned} &\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\\ &\vec{a}+\vec{b}=\overrightarrow{A C}\\ \end{aligned}$
Similarly in $\Delta ABD$
$\begin{aligned} &\overrightarrow{A D}+\overrightarrow{D B}=\overrightarrow{A B}\\ &\vec{b}+D B=\vec{a}\\ &\therefore \vec{a}-\vec{b}=\overrightarrow{D B} \end{aligned}$

Algebra of Vectors Exercise 22.2 Question 4

Answer:

Either $m$ is $0$ or $\vec{a}=0$

Hint:

Use $ab=0$

Given : $m\vec{a}=0$

Solution:

Given, $m\vec{a}=0$

Since if $ab=0$

Either $a=0$ or $b=0$

Therefore, if $m\vec{a}=0$

Either $m=0\: or \: \vec{a}=0$

Algebra of Vectors Exercise 22.2 Question 5

Answer:

True
False
False

Hint:
use vector algebra.
Given :
$\vec{a},\vec{b}$ are two vectors.
Solution
$(i) \; \; \; \; \; \; \: \: \: \vec{a}=-\vec{b}$
$|\vec{a}|=|\vec{b}|$
$\vec{a}=-\vec{b}$
$|\vec{a}|=|-\vec{b}|$
$|\vec{a}|=|-||\vec{b}|$
$|\vec{a}|=1 \cdot|\vec{b}|$
$|\vec{a}|=|\vec{b}|$
$(i)\: \: \: \: \: Is \; \; \; true$
$(ii) \quad|\vec{a}|=|\vec{b}|=\vec{a}=\pm \vec{b}$

$(ii)\: \: is \: \: false$
$(iii) \: \quad|\vec{a}|=|\vec{b}|=\vec{a}=\pm \vec{b}$
$|\vec{a}|=|\vec{b}|$
$a=b$
$(iii)\: false$ .

Algebra of Vectors Exercise 22.2 Question 6

Answer:
$\vec{BA}+\vec{BC}+\vec{CD}+\vec{DA}=2\vec{BA}$
Hint:
Form the triangle in quadrilateral. Use triangle law of inequality.
Given :
ABCD are quadrilateral.
Solution:

In $\Delta ABC,$
By the triangle law of inequality
$\vec{BC}+\vec{CA}=\vec{BA}$
$\vec{CA}=\vec{BA}-\vec{BC}(1)$

Again in $\Delta ADC,$

By triangle law of inequality

$\vec{CA}=\vec{CD}+\vec{DA}.......(2)$

From (1) and (2)

$\begin{aligned} &\overrightarrow{C D}+\overrightarrow{D A}=\overrightarrow{B A}-\overrightarrow{B C} \\ &\overrightarrow{B A}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D A}=\overrightarrow{B A}+\overrightarrow{B A} \\ &\overrightarrow{B A}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D A}=2 \overrightarrow{B A} \end{aligned}$

Algebra of Vectors Exercise 22.2 Question 7

Answer:
We need to prove that
Hint:
Use triangle law of vector.
Given :
ABCDE is a pentagon.
Solution:
Given , ABCDE is a pentagon.
95798

In $\Delta ABC$ ,by tringle law
$\vec{AB}+\vec{BC}=\vec{AC}.......(1)$
In $\Delta ACD$ by tringle law
$\vec{AC}+\vec{CD}=\vec{AD}.......(2)$
In $\Delta AED$ ,by tringle law
$\vec{AD}+\vec{DE}=\vec{AE}......(3)$
or $\vec{AE}+\vec{ED}=\vec{AD}.........(4)$
In $\Delta ADC$ ,by tringle law
$\overrightarrow{A D}+\overrightarrow{D C}=\overrightarrow{A C} \ldots \ldots \ldots (5)$
$(i) \overrightarrow{A D}+\overrightarrow{D C}=\overrightarrow{A C}$
$=\overrightarrow{A C}+\overrightarrow{E C}+E A$
$=\overrightarrow{A E}+\overrightarrow{E A}$
$=\overrightarrow{A E}-\overrightarrow{A E}$
$=0$
$(ii) L.H.S, \overrightarrow{A B}+\overrightarrow{A E}+\overrightarrow{B C}+\overrightarrow{D C}+\overrightarrow{E D}+\overrightarrow{A C}$
$=(\overrightarrow{A B}+\overrightarrow{B C})+(\overrightarrow{A E}+\overrightarrow{E D})+\overrightarrow{A C}+\overrightarrow{D C}$
$=\overrightarrow{A C}+\overrightarrow{A D}+\overrightarrow{D C}+\overrightarrow{A C} \quad [using (1)and(4) ]$
$=\overrightarrow{A C}+\overrightarrow{A C}+\overrightarrow{A C}=3 \overrightarrow{A C} (proved)$

Algebra of Vectors Exercise 22.2 Question 8

Answer:
We need to prove that
Hint:
Used equal and adjacent side law.
Given :
Let 0 be the centre of the octagon with vertices ABCDEFGH.
Solution:
since 0 is the mid-point.
95799

$\begin{aligned} &\overrightarrow{O A}=-\overrightarrow{O E}\\ &\overrightarrow{O A}+\overrightarrow{O E}=0 \ldots \ldots \ldots \text { (1) }\\ &\overrightarrow{O B}=-\overrightarrow{O F}\\ &\overrightarrow{O B}+\overrightarrow{O F}=0 \ldots \ldots \ldots . .\\ &\overrightarrow{O C}=-\overrightarrow{O G}\\ &\overrightarrow{O C}+\overrightarrow{O G}=0 \ldots \ldots \ldots .\\ &\overrightarrow{O P}=-\overrightarrow{O H}\\ &\overrightarrow{O P}+\overrightarrow{O H}=0 \ldots \ldots \ldots \ldots . \text { (4) }\\ \end{aligned}$

Adding (1) (2) (3) and (4)
$\begin{aligned} &\overrightarrow{O A}+\overrightarrow{O E}+\overrightarrow{O B}+\overrightarrow{O F}+\overrightarrow{O C}+\overrightarrow{O G}+\overrightarrow{O P}+\overrightarrow{O H}=\overrightarrow{0} \end{aligned}$

Hence proved.

Algebra of Vectors Exercise 22.2 Question 9

Answer:
We need to prove that
Hint:
Use triangle law.
Given :
$\vec{AD}+\vec{PB}+\vec{PD}=\vec{PC}$
$\vec{AD}+\vec{PB}+\vec{PD}-\vec{PC}$
Solution:
95800

In $\Delta PDC$ ,by triangle law
$\vec{PD}+\vec{DC}=\vec{PC}$
In $\Delta PAB$ ,by triangle law
$\vec{PA}+\vec{PB}=\vec{AB}$
$\therefore$ ABCD is a parallelogram.

Algebra of Vectors Exercise 22.2 Question 10

Answer:
We need to prove that
Hint:
Use triangle law of addition.
Given :
ABCDEF is a hexagon
Solution:
Given ,
ABCDEF is a regular hexagon.
95801

From the triangle law of addition,

$\begin{aligned} &\overrightarrow{A C}+\overrightarrow{C D}=\overrightarrow{A D}\\ \end{aligned}$

$\begin{aligned} &\overrightarrow{A C}+\overrightarrow{A F}=\overrightarrow{A D}\\ \end{aligned}$

$\begin{aligned} &\because|\overrightarrow{C D}|=|\overrightarrow{A F}|\\ \end{aligned}$

$\begin{aligned} &\overrightarrow{C D} \text { parallel to } \overrightarrow{A F}: C D=A F\\ \end{aligned}$

$\begin{aligned} &\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A F}+\overrightarrow{A D}+\overrightarrow{A C}+\overrightarrow{A E}\\ &=\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A D}+\overrightarrow{A C} \quad \because|\overrightarrow{A E}|=|\overrightarrow{E D}|\\ &=2 \overrightarrow{A D}+\overrightarrow{E D}+\overrightarrow{A E A E} \text { parallel to } \overrightarrow{E D} \therefore \overrightarrow{A B}=\overrightarrow{E D}\\ &=2 \overrightarrow{A D}+\overrightarrow{A D}\\ &=3 \overrightarrow{A D} \quad[\overrightarrow{A B}+\overrightarrow{A E}=\overrightarrow{E D}+\overrightarrow{A E}=\overrightarrow{A D}\\ &=3(2 \cdot \overrightarrow{A O}) \quad[O \text { is the mid point and also the mid point of } \mathrm{AD}, \mathrm{OA}=\mathrm{OD}, \mathrm{AD}=2 \cdot \overrightarrow{\mathrm{AO}}]\\ &=6 \overrightarrow{A O} \end{aligned}$

(proved)

Class 12th RD Sharma Chapter 22 Exercise 22.2 Solutions are prepared by a team of experts, considering the latest NCERT textbook and marking schemes. When a student refers to RD Sharma Class 12 Solutions Algebra of Vectors Ex. 22.2, all the concepts will be clear, and a student will better understand the exams. RD Sharma Class 12 Solutions Chapter 22 ex 22.2, when a student refers, the benefits will be the following:

Created by experts:

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

RD Sharma Class 12 Solutions Chapter 22 ex 22.2 are created by subject experts according to the latest marking pattern and CBSE guidelines. Every student must practice RD Sharma Class 12th Exercise 22.2 to score well without difficulty. The topics stated above are explained in these solutions so that even a newcomer can learn and solve them.

2. The best source of preparation:

RD Sharma Class 12th Exercise 22.2 solutions are the best to go for because of their quality. Latest NCERT and CBSE updated solutions make it a brilliant choice. Moreover, the marking scheme is well known to our experts who provide the solutions accordingly, making it easier to score good marks.

3. NCERT based questions:

The questions in exams are usually from the NCERT. Teachers assign question papers based on NCERT textbooks, so learning NCERT concepts and solving questions is necessary. Rd Sharma Class 12th Exercise 22.2 solutions assist students in understanding and learning concepts and solving questions about RD Sharma Class 12 Solutions Chapter 22 ex 22.2.

4. Different ways to solve a question

When a team creates a solution, it is evident that every expert will develop a different way to solve it. As a result, the experts have developed alternative ways to solve a single question making us unique.

5. Benchmark performance

The solutions aid a student's exam performance. RD Sharma Class 12 Solutions Ex. 22.2 covers all of the essential questions that typically appear in exams, allowing students to establish a benchmark score.

6. Free of cost:

Students will find all of these solutions for free at Career360, the best site to visit for all of the benefits related to board exam questions and competitive exams. A student will understand, learn, and perform exceptionally well in exams with Career360. Thousands of students have benefited from these solutions, making Career360 the perfect choice for all students.

RD Sharma Chapter wise Solutions

Frequently Asked Questions (FAQs)

1. What is the algebra of vectors?

Algebra of vectors is a type of algebra in which the components are in vector form, and their algebraic operations comply with vector laws.

2. How many questions are present in this exercise of RD Sharma solutions?

RD Sharma Class 12th Exercise 22.2 has 13 questions that a student needs to practice.

3. What are the concepts that are discussed in RD Sharma Algebra of vectors Class 12th solutions?

The central concepts that are discussed are as follows:

Introduction
Basic Concepts
Types of Vectors
Addition of Vectors
Multiplication of a vector by a scalar

4. Where can I find RD Sharma Solutions for Class 12 Maths Chapter 22 exercise-by-exercise answers?

Students in Class 12 should select appropriate study materials to help them solve textbook problems efficiently. In Career360, the solutions to both chapter and exercise problems are available. It can be referred to by students while solving problems to quickly clear their doubts

5. What are the Vector Addition Laws?

The two main vector addition laws are as follows:

A + B = B + A is a commutative law.

A + (B + C) = (A + B) + C is a Associative Law.