NCERT Solutions for Class 8 Maths Chapter 6 - We Distribute, Yet Things Multiply

NCERT Solutions for Class 8 Maths Chapter 6: Exercise Questions

Question 1. Observe the multiplication grid below. Each number inside the grid is formed by multiplying two numbers. If the middle number of a 3 × 3 frame is given by the expression pq, as shown in the figure, write the expressions for the other numbers in the grid.

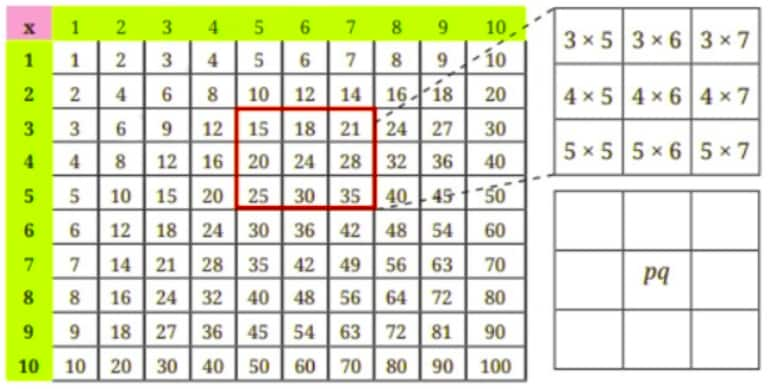
Answer:

Question 2. Expand the following products.
(i) $(3+u)(v-3)$
(ii) $\frac{2}{3}(15+6 a)$
(iii) $(10 a+b)(10 c+d)$
(iv) $(3-x)(x-6)$
(v) $(-5 a+b)(c+d)$
(vi) $(5+z)(y+9)$

Answer:

(i) $(3+u)(v-3)$
$=3 v-9+u v-3 u$
$=u v+3 v-3 u-9$

(ii) $\frac{2}{3}(15+6 a)$
$=\frac{2}{3} \times 15+\frac{2}{3} \times 6 a$
$=10+4 a$

(iii) $(10 a+b)(10 c+d)$
$=100 a c+10 a d+10 b c+b d$

(iv) $(3-x)(x-6)$
$=3 x-18-x^2+6 x$
$=-x^2+9 x-18$

(v) $(-5 a+b)(c+d)$
$=-5 a c-5 a d+b c+b d$

(vi) $(5+z)(y+9)$
$=5 y+45+z y+9 z$
$=5 y+z y+9 z+45$

Question 3. Find 3 examples where the product of two numbers remains unchanged when one of them is increased by 2 and the other is decreased by 4.

Answer:

Let the two numbers be x and y.

According to the question,
$x \times y=(x+2)(y-4)$
$⇒x y=x y-4 x+2 y-8$
$⇒4 x-2 y=-8$
$⇒2 x-y=-4$
$⇒y=2 x+4$

Examples:
1. If $x=1,$ then $y=6 \rightarrow 1 \times 6=6$ and (3) $\times(2)=6$
It satisfies the condition.
2. If $x=2,$, then $y=8 \rightarrow 2 \times 8=16$ and (4) $\times(4)=16$
It satisfies the condition.
3. If $x=5,$ then $y=14 \rightarrow 5 \times 14=70$ and $(7) \times(10)=70$
It satisfies the condition.

Question 4. Expand (i) $\left(a+a b-3 b^2\right)(4+b)$, and (ii) $(4 y+7)(y+11 z-3)$.

Answer:

(i) $\left(a+a b-3 b^2\right)(4+b)$
$=a(4+b)+a b(4+b)-3 b^2(4+b)$
$=4 a+a b+4 a b+a b^2-12 b^2-3 b^3 $
$=4 a+5 a b+a b^2-12 b^2-3 b^3$

(ii) $(4 y+7)(y+11 z-3)$
$=4 y(y+11 z-3)+7(y+11 z-3) $
$=4 y^2+44 y z-12 y+7 y+77 z-21 $
$=4 y^2+44 y z-5 y+77 z-21$

Question 5. Expand (i) $(a-b)(a+b)$, (ii) $(a-b)\left(a^2+a b+b^2\right)$ and (iii) $(a-b)\left(a^3+a^2 b+a b^2+b^3\right)$, Do you see a pattern? What would be the next identity in the pattern that you see? Can you check it by expanding?

Answer:

(i) $(a-b)(a+b)$
$=a^2-b^2$

(i) $(a-b)\left(a^2+a b+b^2\right)$
$=a^3+a^2 b+a b^2-a^2 b-a b^2-b^3$
$=a^3-b^3$

(iii)
$(a-b)\left(a^3+a^2 b+a b^2+b^3\right)$
$=a^4+a^3 b+a^2 b^2+a b^3-a^3 b-a^2 b^2-a b^3-b^4$
$=a^4-b^4$

Here is a clear pattern.
Results are in the form, $a^n -b^n,$ where $n = 2,3,4,...$

So, the next identity:
$(a-b)\left(a^4+a^3 b+a^2 b^2+a b^3+b^4\right)=a^5-b^5$

Question 1. Which is greater: $(a-b)^2$ or $(b-a)^2$ ? Justify your answer.

Answer:

$(b-a)^2=[-(a-b)]^2=(-1)^2(a-b)^2=(a-b)^2 $
So they are equal for every $a, b$.
Squaring removes the (-) sign, so the two expressions are identical.

Example:
$(4-2)^2=(2-4)^2=4$

Question 2. Express 100 as the difference of two squares.

Answer:

We know that $x^2-y^2=(x-y)(x+y)$

If $x=26$ and $y=24$,

$26^2-24^2=(26+24)(26-24)=50\times2=100$

If $x=10$ and $y=0$

Then, $(10+0)(10-0)=10^2-0^2=100$

Question 3. Find $406^2, 72^2, 145^2, 1097^2$, and $124^2$ using the identities you have learnt so far.

Answer:

We know that,
$(a+b)^2=a^2+2ab+b^2$
and $(a-b)^2=a^2-2ab+b^2$

(i) $406^2=(400+6)^2=400^2+2 \times 400 \times6+6^2=160000+4800+36=164836$
(i) $72^2=(70+2)^2=70^2+2\times 70 \times2+2^2=4900+280+4=5184$
(iii) $145^2=(150-5)^2=150^2-2\times 150 \times 5+5^2=22500-1500+25=21025$
(iv) $1097^2=(1100-3)^2=1100^2-2\times1100 \times3+3^2=1210000-6600+9=1203409$
(v) $124^2=(100+24)^2=10000+2 \times100 \times 24+24^2=10000+4800+576=15376$

Question 4. Do Patterns 1 and 2 hold only for counting numbers? Do they hold for negative integers as well? What about fractions? Justify your answer.

Answer:

Pattern 1:
$\begin{aligned} & (a+b)^2=a^2+2 \mathrm{ab}+b^2 \\ & (a-b)^2=a^2-2 \mathrm{ab}+b^2\end{aligned}$

Pattern 2:
$a^2-b^2=(a+b) \times(a-b)$

These are algebraic identities that hold not only for counting numbers, but also for,

• Negative integers
• Fractions (rational numbers)
• Decimals, irrationals, even complex numbers

Negative numbers check:

Let $a=-3, b=5$ :
Pattern 1:
$(a+b)^2=(2)^2=4$,
RHS $=9-30+25=4$
Pattern 2:
$a^2-b^2=9-25=-16,$
RHS $=(a+b)(a-b)=(2)(-8)=-16$

Fractions check:

Let $a=\frac{1}{2}, b=-\frac{1}{3}$ :
Pattern 1:
$(a-b)^2=\left(\frac{1}{2}+\frac{1}{3}\right)^2=\left(\frac{5}{6}\right)^2=\frac{25}{36}$
RHS $ =\frac{1}{4}+\frac{1}{3}+\frac{1}{9}=\frac{25}{36}$
Pattern 2:
$a^2-b^2=\frac{1}{4}-\frac{1}{9}=\frac{5}{36}$
RHS $=(a+b)(a-b)=\frac{1}{6} \times \frac{5}{6}=\frac{5}{36}$

Question 1. Compute these products using the suggested identity.
(i) $46^2$ using Identity 1 A for $(a+b)^2$
(ii) $397 \times 403$ using Identity 1 C for $(a+b)(a-b)$
(iii) $91^2$ using Identity 1 B for $(a-b)^2$
(iv) $43 \times 45$ using Identity 1 C for $(a+b)(a-b)$

Answer:

(i)
Lets take $a=40, b=6$ :
$46^2=(40+6)^2=40^2+2 \times 40 \times 6+6^2=1600+480+36=2116$

(ii)
Lets take $a=400, b=3$ :
$397 \times 403=(400-3)(400+3)=400^2-3^2=160000-9=159991$

(iii)
Lets take $a=100, b=9$ :
$91^2=(100-9)^2=10000-2 \cdot 100 \cdot 9+9^2=10000-1800+81=8281$

(iv)
Here $a=44, b=1$:
$43 \times 45=(44-1)(44+1)=44^2-1^2=1936-1=1935$

Question 2. Use either a suitable identity or the distributive property to find each of the following products.
(i) $(p-1)(p+11)$
(ii) $(3 a-9 b)(3 a+9 b)$
(iii) $-(2 y+5)(3 y+4)$
(iv) $(6 x+5 y)^2$
(v) $\left(2 x-\frac{1}{2}\right)^2$
(vi) $(7 p) \times(3 r) \times(p+2)$

Answer:

(i) $(p-1)(p+11)$
Using distributive property:
$=p^2+11 p-p-11$
$=p^2+10 p-11$

(ii) $(3 a-9 b)(3 a+9 b)$
Using Difference of squares:
$=(3 a)^2-(9 b)^2$
$=9 a^2-81 b^2$

(iii) $-(2 y+5)(3 y+4)$
$=-[(2 y)(3 y)+(2 y)(4)+(5)(3 y)+(5)(4)]$
$=-[6 y^2+8 y+15 y+20]$
$=-[6 y^2+23 y+20]$
$=-6 y^2-23 y-20$

(iv) $(6 x+5 y)^2$
Using the square of sum:
$=(6 x)^2+2(6 x)(5 y)+(5 y)^2$
$=36 x^2+60 x y+25 y^2$

(v) $\left(2 x-\frac{1}{2}\right)^2$
Using the square of difference:
$=(2 x)^2-2(2 x)\left(\frac{1}{2}\right)+\left(\frac{1}{2}\right)^2$
$=4 x^2-2 x+\frac{1}{4}$

(vi) $(7 p) \times(3 r) \times(p+2)$
Using stepwise multiplication:
$=21 p r(p+2)$
$=21 p^2 r+42 p r$

Question 3. For each statement, identify the appropriate algebraic expression(s).
(i) Two more than a square number.

$2+s \quad(s+2)^2 \quad s^2+2 \quad s^2+4 \quad 2 s^2 \quad 2^2 s$

(ii) The sum of the squares of two consecutive numbers

$\begin{array}{llll}m^2+n^2 & (m+n)^2 & m^2+1 \quad m^2+(m+1)^2 \\ m^2+(m-1)^2 & (m+(m+1))^2 & (2 m)^2+(2 m+1)^2\end{array}$

Answer:

(i)
Let a number be $x$.
According to the question,
$s^2+2$

Hence, the correct answer is $s^2+2$.

(ii)
Let the first number be $m$, so the next is $m+1$.
According to the question,
$m^2+(m+1)^2$

Hence, the correct answer is $m^2+(m+1)^2$.

Question 4. Consider any 2 by 2 square of numbers in a calendar, as shown in the figure.

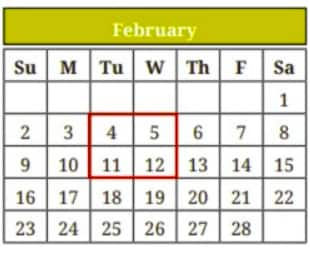
Find products of numbers lying along each diagonal $-4 \times 12=48$, $5 \times 11=55$. Do this for the other 2 by 2 squares. What do you observe about the diagonal products? Explain why this happens.
Hint: Label the numbers in each 2 by 2 square as

Answer:

1st example:

Products of diagonals are:
$2\times10=20$ and $3\times9=27$

2nd example:

Products of diagonals are:
$7\times15=105$ and $8\times 14=112$

We can see that the second diagonal product is always 7 more than the first.

If we take the 1st number as a, then the table becomes:

Product of diagonals:
$a(a+8)=a^2+8a$
And $(a+1)(a+8)=a^2+a+8a+8=a^2+9a+8$
$\text { Difference }=\left[a^2+8 a+7\right]-\left[a^2+8 a\right]=7$
7 is the step size down a column in our grid, so the difference between diagonal products is constant.

Question 5. Verify which of the following statements are true.
(i) $(k+1)(k+2)-(k+3)$ is always 2.
(ii) $(2 q+1)(2 q-3)$ is a multiple of 4.
(iii) Squares of even numbers are multiples of 4, and squares of odd numbers are 1 more than multiples of 8.
(iv) $(6 n+2)^2-(4 n+3)^2$ is 5 less than a square number.

Answer:

(i) $(k+1)(k+2)-(k+3)$
$=k^2+3 k+2-(k+3)$
$=k^2+2 k-1$,
which is not constant 2.
Hence, the statement is False.

(ii) $(2 q+1)(2 q-3)$ is a multiple of 4 .
$=4 q^2-4 q-3$
$=4\left(q^2-q\right)-3$
It is not a multiple of 4 as there is an extra (-3).
Hence, the statement is False.

(iii) Squares of even numbers are multiples of 4, and squares of odd numbers are 1 more than multiples of 8.

Let's take an example.

Let number $=2 m$. Square $=(2 m)^2=4 m^2$, which is a multiple of 4.
Let number $=2 m+1$. Square $=(2 m+1)^2=4m^2+4m+1=4 m(m+1)+1$.
Since $m(m+1)$ is even, we can write $m(m+1)=2 t$,
so square $=8 t+1$. That is 1 more than a multiple of 8.
Hence, the statement is True.

(iv) $(6 n+2)^2-(4 n+3)^2$ is 5 less than a square number.

$(6 n+2)^2-(4 n+3)^2$
$=(6 n+2-4 n-3)(6 n+2+4 n+3)$
$=(2 n-1)(10 n+5)$
$=5(2 n-1)(2 n+1)$
$=20 n^2-5 $
$20n^2$ is not a square number for any values of $n$.
Hence, the statement is False.

Question 6. A number leaves a remainder of 3 when divided by 7, and another number leaves a remainder of 5 when divided by 7. What is the remainder when their sum, difference, and product are divided by 7?

Answer:

The 1st number = $7+3=10$

and 2nd number $=7+5=12$

Sum = 10 + 12 = 22, when divided by 7 leaves a remainder of 1.

Difference = 10 - 12 = - 2, when divided by 7 leaves a remainder of 5.

[In this case, we will use the definition of division with remainder for negative numbers.

The largest multiple of 7 less than or equal to -2 is -7. This is because $7 \times-1=-7$

So, remainder $=-2-(-7)=-2+7=5$]

Product = $10\times12=120$, when divided by 7 leaves a remainder of 1.

Question 7. Choose three consecutive numbers, square the middle one, and subtract the product of the other two. Repeat the same with the other sets of numbers. What pattern do you notice? How do we write this as an algebraic equation? Expand both sides of the equation to check that it is a true identity.

Answer:

Let three consecutive numbers be $n-1, n, n+1$.
According to the question,
$n^2-(n-1)(n+1)=n^2-\left(n^2-1\right)=1$

Other example:
Let three consecutive numbers be $n+1, n+2, n+3$.
$(n+2)^2-(n+1)(n+3)=n^2+4n+4-n^2-n-3n-3=1$

The Pattern shows that the result is always 1.
Algebraic identity: $n^2-(n-1)(n+1)=1$.
Expanding both sides shows it is true.

Question 8. What is the algebraic expression describing the following steps:
Add any two numbers. Multiply this by half of the sum of the two numbers? Prove that this result will be half of the square of the sum of the two numbers.

Answer:

Let the two numbers be $x$ and $y$.

According to the question,

$(x+y) \times \frac{1}{2}(x+y)$

$=\frac{1}{2}(x+y)^2$

So the result equals half the square of the sum.

Now,

$\frac{1}{2}\left(x^2+2 x y+y^2\right)$

$=\frac{1}{2} x^2+x y+\frac{1}{2} y^2$

which matches the direct expansion.

Question 9. Which is larger? Find out without fully computing the product.
(i) $14 \times 26$ or $16 \times 24$
(ii) $25 \times 75$ or $26 \times 74$

Answer:

(i)
$14 \times 26$
$=(20-6)(20+6)$
$=20^2-6^2$

$16 \times 24$
$=(20-4)(20+4)$
$=20^2-4^2$

So, clearly $16 \times 24$ is larger.

(ii)

$25 \times 75$
$=(50-25)(50+25)$
$=50^2-25^2$

$26 \times 74$
$=(50-24)(50+24)$
$=50^2-24^2$

So, clearly $26 \times 74$ is larger.

Question 10. A tiny park is coming up in Dhauli. The plan is shown in the figure. The two square plots, each of area $g^2$ sq. ft, will have a green cover. All the remaining area is a walking path $w$ ft . wide that needs to be tiled. Write an expression for the area that needs to be tiled.

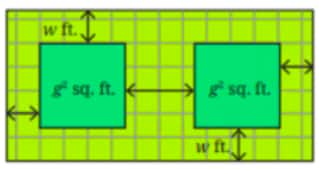
Answer:

Outer rectangle width(From left) $=w+g+w+g+w=2 g+3 w$
Outer rectangle height(From Up to Down) $=w+g+w=g+2 w$

Total outer area $=(2 g+3 w)(g+2 w)=2g^2+3gw+4gw+6w^2=2g^2+6w^2+7gw$
Green area (two squares) $=g^2+g^2=2 g^2$

$\therefore$ Required area that needs to be tiled = $2g^2+6w^2+7gw-2g^2=6w^2+7gw=w(6w+7g)$

Question 11. For each pattern shown below,
(i) Draw the next figure in the sequence.
(ii) How many basic units are there in Step 10?
(iii) Write an expression to describe the number of basic units in Step $y$.

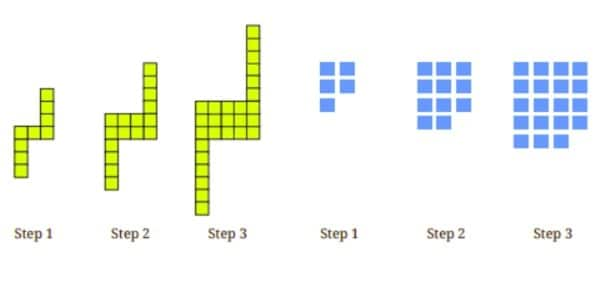
Answer:

(i)
1st pattern:
Step 1: 9 units
Step 2: 16 units
Step 3: 27 units

Differences between terms: $+7,+11,+15, \ldots$ (increase by 4 ).
nth term: $a_n=2 n^2+n+6$, where $n=1,2,3,...$
4th term: $a_4=2\times 4^2+4+6=42$


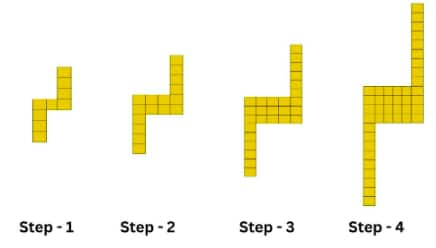
(ii)
10th term: $a_{10}=2\times(10)^2+10+6=216$

(iii)
yth term: $a_y=2 y^2+y+6$, where $y=1,2,3,...$

(i)
2nd pattern:

Step 1: 5 units
Step 2: 11 units
Step 3: 19 units
Differences: $+6,+8,+10, \ldots$ (increase by 2 ).
nth term: $b_n=n^2+3 n+1$, where $n=1,2,3,....$
4th term: $b_4=4^2+3\times4+1=29$

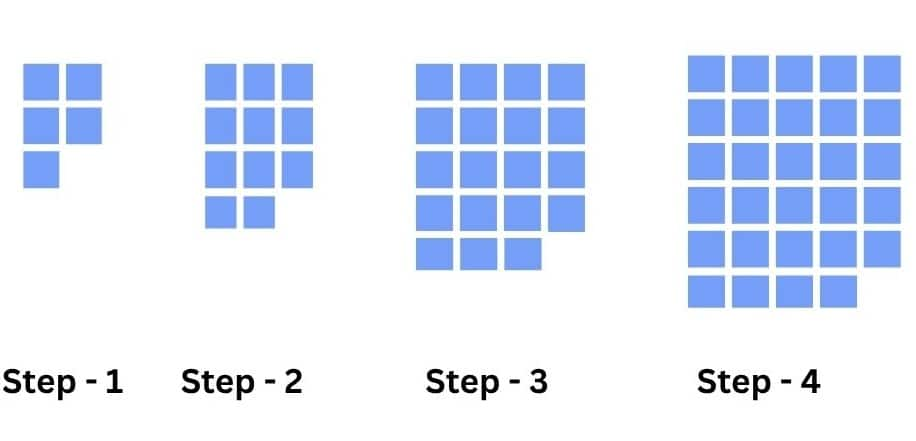
(ii)
10th term: $b_{10}=10^2+3\times(10)+1=131$

(iii)
yth term: $b_y=y^2+3 y+1$, where $y=1,2,3,....$

We Distribute, Yet Things Multiply Class 8 Chapter 6: Topics

Here are the topics covered in NCERT Solutions for Class 8 Chapter 6 We Distribute, Yet Things Multiply:

• Some Properties of Multiplication
• Fast Multiplications Using the Distributive Property
• Special Cases of the Distributive Property
• Mind the Mistake, Mend the Mistake
• This Way or That Way, All Ways Lead to the Bay

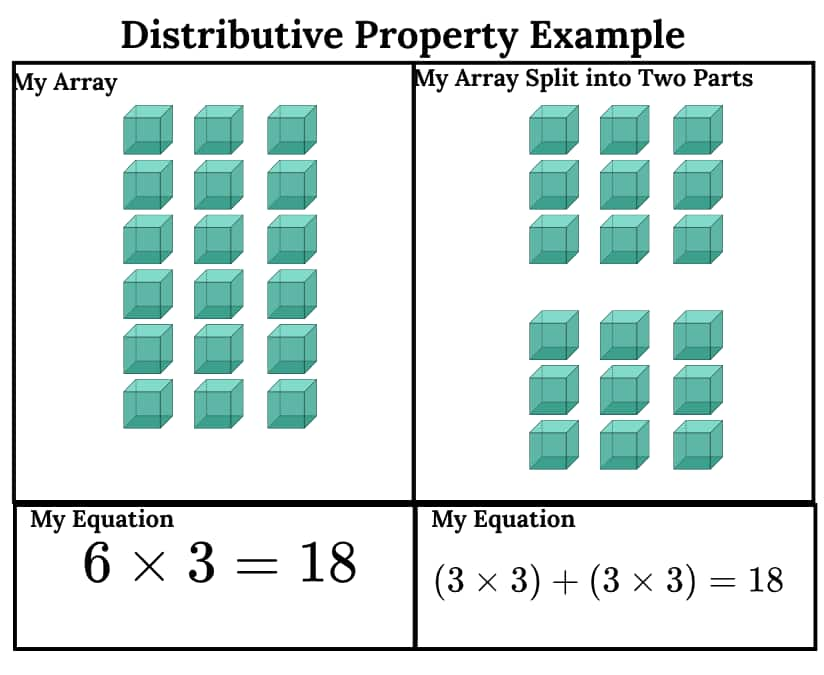
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: Important Formulae

• $(a+b)^2=a^2+2 \mathrm{ab}+b^2$
• $(a-b)^2=a^2-2 \mathrm{ab}+b^2$
• $a^2-b^2=(a+b) \times(a-b)$
• $(a+b)(c+d)=a c+a d+b c+b d$
• $(k \cdot m)^2=k^2 \cdot m^2$
• If numbers are $n+1, n+2, n+3$, then: $(n+2)^2-(n+1)(n+3)=1$

NCERT Solutions for Class 8 Mathematics - Chapter Wise

All NCERT Class 8 Maths solutions can be accessed through the links provided here.

NCERT Books and the NCERT Syllabus

The links below will help you access the NCERT books and the complete NCERT syllabus for Class 8 quickly and easily.

• NCERT Books Class 8 Maths
• NCERT Syllabus Class 8 Maths
• NCERT Books Class 8
• NCERT Syllabus Class 8