Mathematics Of Optics: Understanding Light And Its Interactions With Matter

Have you ever wondered about the incredible phenomena of light and how it interacts with the world around us? From the colours that paint our surroundings to the way we perceive objects, light plays a fundamental role in our daily lives. It turns out that understanding the behaviour of light and its interactions with matter requires a mathematical framework that reveals the secrets of optics.

In this article, we will explore how light behaves and interacts with the world around us. We'll learn about how light travels, reflects off surfaces, bends when passing through objects, and interacts with different materials. By using maths, such as geometry and calculus, we can understand and explain these behaviours. These concepts are essential in designing lenses, mirrors, and other optical devices. We'll also discover how light interacts with different substances, which has practical applications in fields like medicine, telecommunications, and astronomy.

Understanding Light

Dual Nature Of Light

The dual nature of light refers to its ability to exhibit characteristics of both particles and waves. This duality is explained by quantum mechanics, which describes light as consisting of discrete particles called photons, while also having wave-like properties such as interference and diffraction. This concept is represented by the wave-particle duality principle, which states that particles like photons can behave as waves under certain circumstances.

Reflection

Reflection occurs when light rays bounce off a surface. The behaviour of light during reflection can be mathematically described using the law of reflection. According to this law, the angle of incidence (θ_i) is equal to the angle of reflection (θ_r), measured with respect to the normal to the surface.

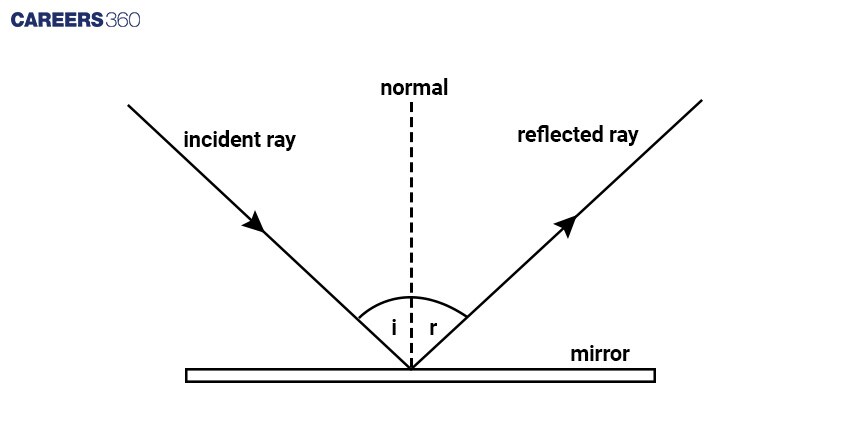
This relationship can be expressed as: θ_i = θ_r

How mathematics helps to find this law of reflection. let's discuss

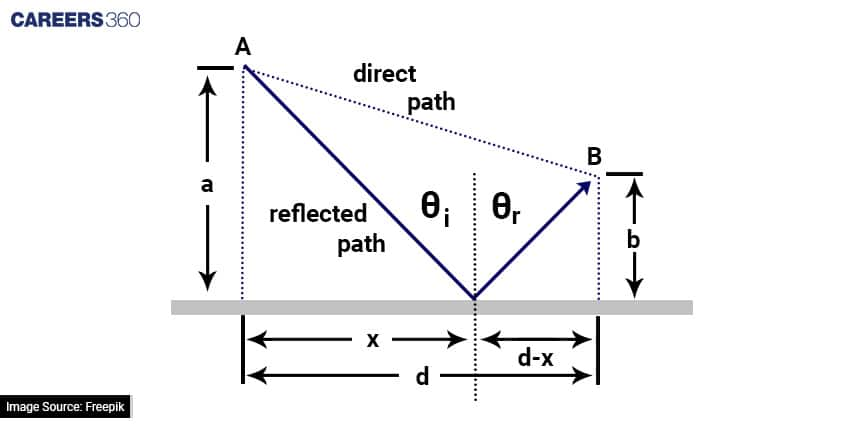
Consider a light ray reflecting from the surface as given below.

Also Read | Ideal Gas Laws: Mathematical Relationships In Gaseous Systems

The path length A to B is given by

L = √[a²+x²] + √[b²+(d-x)²]

Since the speed of light is constant therefore the minimum path is simply the minimum distance path.

We can find this minimum path using the derivative of L with respect to x is zero

We are using the Chain Rule of differentiation.

y = f(g(x)) ⇒ y' = f'(g(x))g'(x)

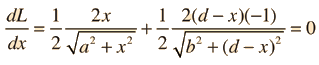
This equation reduced as

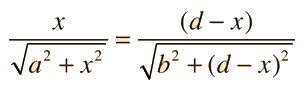
Which is sin θ_i = sin θ_r

Therefore θ_i = θ_r .

Refraction

Refraction occurs when light rays pass through a transparent medium, causing a change in their speed and direction. The behaviour of light during refraction can be mathematically described using Snell's law. According to Snell's law, the ratio of the sines of the angles of incidence (θi) and refraction (θr) is equal to the ratio of the speeds (v) of light in the two mediums:

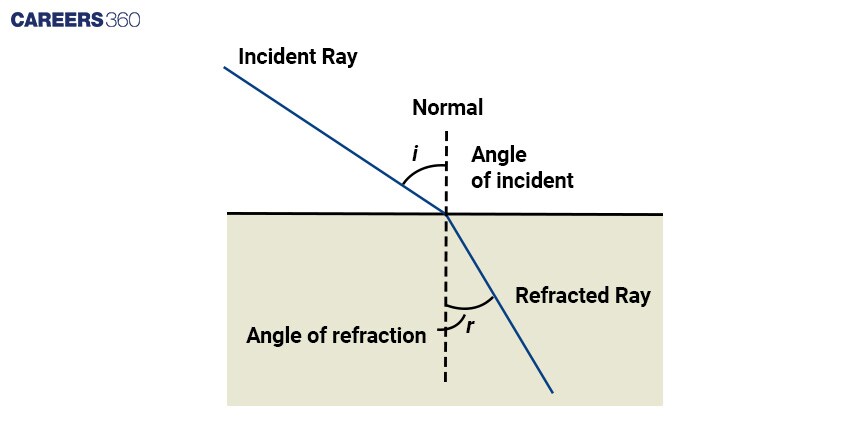
Mathematically the relation can be expressed as n₁sin θ_i = n₂sin θ_r

Also Read | How Do Plants Synthesise Hormones Without An Endocrine System?

Where n₁ and n₂ are the refractive indices of the two mediums. This equation allows us to calculate the angle of refraction based on the incident angle and the refractive indices of the mediums involved.

For example, if a light is incident from the air (with a refractive index of approximately 1) onto a medium with a refractive index of 1.5, and the incident angle is 30 degrees, we can calculate the angle of refraction using Snell's law:

n₁sin θ_i = n₂sin θ_r

1 sin 30 = 1.5 sin θ_r

We know that sin 30 = 1/2

1/2 = 1.5 sin θ_r

sin θ_r = 0.5/1.5

θ_r = sin^-1(0.5/1.5)

θ_r = 19.47 degrees

Diffraction

Diffraction refers to the bending or spreading of light waves as they encounter obstacles or pass through narrow openings. This phenomenon can be mathematically described using the principles of wave interference. The diffraction pattern resulting from a narrow slit can be determined using the following equation:

θ = λ / a

Where θ represents the angle between the central maximum and a specific diffraction order, λ is the wavelength of light, and a is the width of the slit. This equation allows us to calculate the angles at which the bright and dark fringes of the diffraction pattern appear.

Interference

Interference occurs when two or more light waves overlap, leading to constructive or destructive interference. The interference pattern can be mathematically described using wave superposition. The principle of superposition states that the displacement of the resulting wave at a given point is equal to the sum of the individual displacements caused by each wave.

For example, when two coherent light sources with the same frequency and a constant phase difference interfere, the

Regenerate response

Optical Instruments

Mirrors

Mirrors are essential optical devices that rely on the principles of reflection to manipulate and redirect light. Understanding the mathematical concepts behind mirrors allows us to precisely predict and control the behaviour of light as it interacts with reflective surfaces.

When light strikes a mirror, it follows the law of reflection, which states that the angle of incidence is equal to the angle of reflection. This principle can be mathematically expressed as:

θ_i = θ_r

where θ_i represents the angle of incidence and θ_r represents the angle of reflection.

The mirror equation relates the object distance (u), image distance (v), and the focal length (f) of a mirror. It can be expressed as:

1/f = 1/v + 1/u

where,

f = Distance between the mirror and its focal point (focal length).

u = Distance between the mirror and the object being reflected (object distance).

v = Distance between the mirror and the image formed (image distance).

This equation is derived from the principles of reflection and geometry which is applicable to both concave and convex mirrors. However, for concave mirrors, the focal length is considered positive (+) because the focal point is in front of the mirror, while for convex mirrors, the focal length is considered negative (-) because the focal point is behind the mirror.

Magnification M = -v/u

The negative sign indicates whether the image formed is upright (positive magnification) or inverted (negative magnification) compared to the object.

The magnification formula allows us to determine the relative size of the image with respect to the object. A magnification greater than 1 indicates that the image is larger than the object, while a magnification less than 1 indicates that the image is smaller.

In addition to the mirror equation and magnification formula, another important concept related to mirrors is the mirror power. The mirror power (P) represents the ability of a mirror to converge or diverge light. It is defined as the reciprocal of the focal length and is expressed in diopters (D).

P = 1/f

The positive value of mirror power indicates a converging mirror (concave mirror), while the negative value indicates a diverging mirror (convex mirror). The greater the absolute value of the mirror power, the stronger the convergence or divergence of the mirror.

Consider a concave mirror with a focal length of 15 cm. We want to determine the magnification and power of the mirror when an object is placed 30 cm away from it. Find the magnification and power of a mirror.

Solution:

Given: f = 15 cm (focal length) u = -30 cm (object distance, negative sign indicates that the object is in front of the mirror)

Using the mirror formula, we can solve for v:

1/f = 1/v - 1/u

1/15 = 1/v - 1/-30

Simplifying the equation gives:

1/v = 1/15 - 1/-30

1/v = 2/30 + 1/30

1/v = 3/30

v = 30/3 cm

v = 10 cm

So, the image is formed at a distance of 10 cm from the mirror.

Magnification (m) = -v/u

m = -10 cm / -30 cm

m = 1/3

Therefore, the magnification is 1/3, which means the image formed by the mirror is one-third the size of the object.

To find the power of the mirror, we can use the equation:

Power (P) = 1/f

P = 1/15 cm^-1

P = 0.067 cm^-1

So, the power of the concave mirror is 0.067 cm^-1, indicating that it has a converging effect on light.

Also Read | Understand Newton’s Law Of Motion Better Via 'Gravity' The Movie

Lens

Lenses are another crucial optical device used in various applications, from eyeglasses to microscopes and cameras. Lenses utilise the principles of refraction to focus or disperse light, allowing us to manipulate the direction and convergence of light rays.

There are two primary types of lenses: convex (converging) lenses and concave (diverging) lenses. Convex lenses are thicker at the centre and cause light rays to converge, while concave lenses are thinner at the centre and cause light rays to diverge.

The behaviour of light as it passes through a lens can be mathematically described using the lens formula:

1/f = 1/v - 1/u

where f represents the focal length of the lens, v represents the distance of the image from the lens, and u represents the distance of the object from the lens. This equation is derived from the principles of refraction and is applicable to thin lenses.

The lens formula allows us to calculate the position and size of the image formed by a lens, based on the characteristics of the lens and the object being observed. It helps us understand the formation of both real and virtual images and determines whether the image is magnified or diminished.

For example, let's consider a convex lens with a focal length of 10 cm. If an object is placed 20 cm away from the lens, we can use the lens formula to calculate the image distance:

1/f = 1/v - 1/u

1/10 = 1/v - 1/20

Simplifying the equation gives:

1/v = 1/10 + 1/20

1/v = 3/20

v = 20/3 cm

In this case, the image is formed at a distance of approximately 6.67 cm from the lens.

Furthermore, the lens formula also allows us to determine the magnification produced by a lens, which is given by the equation:

magnification M = -v/u

where the negative sign indicates whether the image is inverted or upright.

By understanding the mathematical concepts and formulas associated with mirrors and lenses, we can design optical systems that meet specific requirements. These calculations aid in the development of accurate imaging systems, such as telescopes, microscopes, and cameras, ensuring that the images produced are clear, focused, and properly aligned.

Interactions With Matter

Light interacts with different substances in various ways, and understanding these interactions has practical applications in fields such as medicine, telecommunications, and astronomy.

One fundamental aspect of light's interaction with matter is absorption. Different substances have specific properties that determine how much light they absorb at different wavelengths. This knowledge is crucial in fields like medicine, where we use light absorption to analyse biological samples or perform non-invasive imaging techniques. For example, in a medical procedure called pulse oximetry, a device measures the absorption of light by oxygenated and deoxygenated blood to determine the oxygen levels in a patient's blood.

Another important aspect is light transmission. Some materials allow light to pass through them with little or no absorption, while others may block or scatter the light. Understanding how light transmits through materials is vital in telecommunications, where we use fibre-optic cables to transmit data over long distances. These cables are designed to have minimal light loss and use the principle of total internal reflection to guide light through the cable, allowing for fast and efficient data transmission.