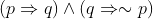Mathematical Reasoning Makes The Truth Table Easier

Articles
Mathematical Reasoning Makes The Truth Table Easier

Mathematical Reasoning Makes The Truth Table Easier

Ramraj SainiUpdated on 02 Jun 2022, 04:01 PM IST

Mathematical Reasoning or the Principle of Mathematical Reasoning is a branch of mathematics where we study the truth values of a mathematical statement. Truth values i.e true and false symbolised by T and F respectively, are binary values therefore sometimes denoted by 1 and 0. In the JEE Main exam, these questions are low-hanging fruits for students. This article comprises concepts related to mathematical reasoning and truth tables including an explanation of concepts using previous year's questions of JEE Main.

Mathematical Reasoning Makes The Truth Table Easier

Mathematical Reasoning(Image: Shutterstock)

Mathematical Statement

Consider the statement “(x+1) is a prime number”

This statement can either be true or false depending on the value of x. This type of ambiguous statement can’t be accepted as a mathematical statement. Thus a statement can only be accepted mathematically if it is either true or false but can not be both at the same time.

Using connectives we can connect two or more statements. For example, she has beautiful eyes and he is intelligent. Here “and” is the connective, ‘she has beautiful eyes’ and ‘he is intelligent’ are component statements and the resultant statement is called a compound statement.

Mathematical Reasoning And Truth Table

A truth table is an arrangement of truth values of compound statements i.e when is a compound statement true or false depending on different truth values of component statements. Some connectives are listed below with Venn diagrams and a corresponding truth table.

Logical Connectives With Venn Diagram, Symbol, Term Used, Truth Table

Logical Connective

Venn Diagram

Symbol Used

Term Used

Truth Table

A or B

A∨B

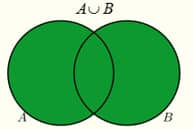
1654058637250

∨

Disjunction

A	B	A∨B
T	T	T
T	F	T
F	T	T
F	F	F

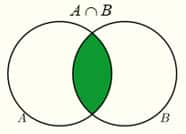
AND

A and B

A∧B

1654058637772

∧

Conjunction

A	B	A∧B
T	T	T
T	F	F
F	T	F
F	F	F

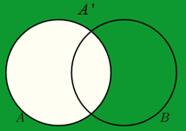
Not

∼A

1654058637636

∼

Negation

A	∼A
T	F
T	F
F	T
F	T

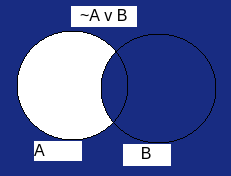
If……Then

If A then B

A→B

= ∼A∨B

1654058637081

→

⇒

Implication

A	B	A→B
T	T	T
T	F	F
F	T	T
F	F	T

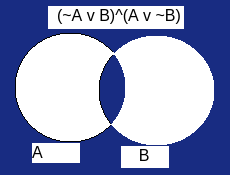
If And Only If

A↔B

= (∼A∨B)∧(A∨∼B)

1654058636807

↔

⇔

Double Implication

A	B	A↔B
T	T	T
T	F	F
F	T	F
F	F	T

Basic Important Points:

The following important points or properties can be used while solving reasoning questions.

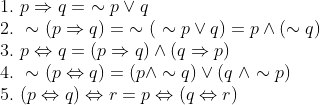
1654058637430

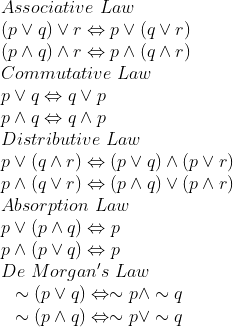
1654058655571

Previous Years Questions To Understand The Concepts

The Joint Entrance Exam or JEE Main is held in multiple sessions. Analyzing the previous year's question papers, students will realise that one or two questions are repeatedly being asked from mathematical reasoning. There are mainly six types of questions that are asked repeatedly, they are mentioned below.

The equivalent of a mathematical statement
Negation of mathematical statement
Find the truth value of a given mathematical statement
Tautology
Fallacy
The contrapositive of statement

Q-1: (JEE Main - 2021)

The Boolean expression is equivalent to:

$\sim \mathrm{q}$
$\mathrm{q}$
$\mathrm{p}$
$\sim \mathrm{p}$

Solution:

$\equiv \left ( \sim p\vee q \right )\wedge \left ( \sim q\vee \sim p \right )$

$\equiv \sim p\vee \left ( q\wedge \sim q \right )$

$\equiv \sim p$

Concepts Used:

p→q = ∼p v q
q→∼p = ∼q v ∼p
Distributive law: p v (q ∧ r) = (p v q) ∧ (p v r)

Alternative method: students can use the truth table to solve this.

p	q	p→q	∼p	∼q	q→∼p = ∼q v ∼p
T	T	T	F	F	F	F
T	F	F	F	T	T	F
F	T	T	T	F	T	T
F	F	T	T	T	T	T

Truth values of ∼p and 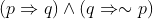1654058781963 are the same, thus correct answer is ∼p.

Alternative method: Venn diagram

Mathematical Reasoning Equation	Venn Diagram
p→q = ∼p v q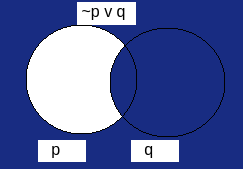
q →∼p = ∼q v ∼p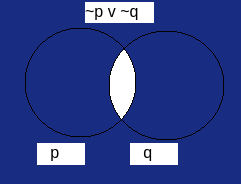

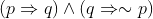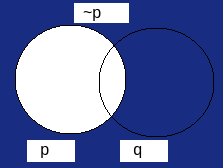It can be observed that the Venn diagram of 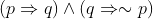1654058806646 is the same as the Venn diagram of ∼p.

Q-2: (JEE Main - 2021)

Negation of the statement $(p \vee r) \Rightarrow(q \vee r)$ is:

$\sim \mathrm{p} \wedge \mathrm{q} \wedge \sim \mathrm{r}$
$\sim \mathrm{p} \wedge \mathrm{q} \wedge \mathrm{r}$
$\mathrm{p} \wedge \sim \mathrm{q} \wedge \sim \mathrm{r}$
$\mathrm{p} \wedge \mathrm{q} \wedge \mathrm{r}$

Solution:

$p\Rightarrow q\\$ is equivalent to $\sim p \vee q$

$\equiv (p \vee r) \wedge(\sim q \wedge \sim r) \\$

$\equiv ((p \vee r) \wedge(\sim r)) \wedge \sim q \\$

$\equiv (p \wedge \sim r) \vee(r \wedge \sim r) \wedge \sim q$

$\equiv p\wedge \sim r\wedge\sim q$

Concept used:

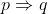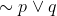
$p\Rightarrow q\\$ is equivalent to $\sim p \vee q$
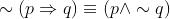
De morgan’s law: ∼(p v q) = ∼p ∧ ∼q
Associative law: (p ∧ q) ∧ r = (p ∧ r) ∧ q
Distributive law: (p v q) ∧ r = (p ∧ r) v (q ∧ r)

Similar to the previous question, we can also solve this question using truth table and Venn diagram method.

Q-3 : (JEE Main - 2021)
If the truth value of the Boolean expression 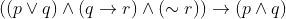$\left ( \left ( p\vee q \right )\wedge \left ( q\rightarrow r \right ) \wedge \left ( \sim r \right )\right )\rightarrow \left ( p\wedge q \right )$ is false, then the truth values of the statements p,q,r respectively can be:

F T F
T F F
T F T
F F T

Solution:

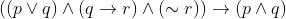
$\left ( \left ( p\vee q \right )\wedge \left ( q\rightarrow r \right ) \wedge \left ( \sim r \right )\right )\rightarrow \left ( p\wedge q \right )$

For this to be false.

$p\wedge q\equiv False\: and.$

$\left ( p\vee q \right )\wedge \left ( q\rightarrow r \right ) \wedge \left ( \sim r \right )\equiv True.$

$\Rightarrow$ At least one of p or q is false and $p\vee q\equiv true\, and\: q\rightarrow r\equiv true\, and \sim r\equiv true.$

$\Rightarrow$ At least one of p or q is false and $\sim r\equiv true\Rightarrow r$ is false and $q\rightarrow r$ is true $\Rightarrow q$ is false. $p\vee q\, is\, true\Rightarrow p$ is true.

$\therefore p,q,r\equiv T\; F\; F$

Q-4 (JEE Main - 2020)

Which of the following statements is a tautology?

$\sim (p\wedge \sim q)\rightarrow p\vee q$
$\sim (p\vee \sim q)\rightarrow p\wedge q$
$p\vee (\sim q)\rightarrow p\wedge q$
$\sim (p\vee \sim q)\rightarrow p\vee q$

Solution:

Tautology: A compound statement is called tautology if it is always true for all possible truth values of its component statement.

For example, ( p ⇒ q ) ∨ ( q ⇒ p )

Truth Table

$\sim (p\wedge \sim q)\rightarrow p\vee q$

∼(p∧∼q)→p∨q = (p∧∼q)∨(p∨q)

p	q	∼p	∼q	p∧∼q	∼(p∧∼q)	p∨q	∼(p∧∼q)→p∨q
T	T	F	F	F	T	T	T
T	F	F	T	T	F	T	T
F	T	T	F	F	T	T	T
F	F	T	T	F	T	F	F

$\sim (p\vee \sim q)\rightarrow p\wedge q$

∼(p∨∼q)→p∧q = (p∨∼q) ∨ p∧q

p	q	∼p	∼q	p∨∼q	∼(p∨∼q)	p∧q	∼(p∨∼q)→p∧q
T	T	F	F	T	F	T	T
T	F	F	T	T	F	F	T
F	T	T	F	F	T	F	F
F	F	T	T	T	F	F	T

$p\vee (\sim q)\rightarrow p\wedge q$

p∨(∼q)→p∧q = ∼(p∨∼q)∨(p∧q)

p	q	∼p	∼q	p∨∼q	∼(p∨∼q)	p∧q	p∨(∼q)→p∧q
T	T	F	F	T	F	T	T
T	F	F	T	T	F	F	F
F	T	T	F	F	T	F	T
F	F	T	T	T	F	F	F

$\sim (p\vee \sim q)\rightarrow p\vee q$

∼(p∨∼q)→p∨q = (p∨∼q)∨(p∨q)

p	q	∼p	∼q	p∨∼q	∼(p∨∼q)	p∨q	∼(p∨∼q)→p∨q
T	T	F	F	T	F	T	T
T	F	F	T	T	F	T	T
F	T	T	F	F	T	T	T
F	F	T	T	T	F	F	T

We can observe that in only option (d) all the truth value are true therefore option (d) $\sim (p\vee \sim q)\rightarrow p\vee q$ is a tautology.

Concept used:

p→q = ∼p v q
De morgan’s law: ∼(p v q) = ∼p ∧ ∼q
De morgan’s law: ∼(p ∧ q) = ∼p v ∼q

Q-5: (JEE Main - 2021)

Consider the two statements:

is a tautology.

$\left ( S2 \right ):\left ( p\wedge \sim q \right )\wedge \left ( \sim p\vee q \right )$ is a fallacy. Then?

only (S1) is true.
both (S1) and (S2) are false.
only (S2) is true.
both (S1) and (S2) are true.

Solution:

Contradiction (fallacy)

A compound statement is a contradiction if it is always false for all possible truth values of its component statement.

For example, ∼( p ⇒ q ) ∨ ( q ⇒ p )

$S1 : \left ( p\rightarrow q \right )\vee \left ( \sim q\rightarrow p \right )$

$\equiv \left ( \sim p\vee p \right )\vee q$

$\equiv t \vee q$

$\equiv t$

$S2:\left ( p\wedge \sim q \right )\wedge \left ( \sim p\vee q \right )$

$\equiv \left ( p\wedge \sim q \right )\wedge \sim \left ( p\wedge \sim q \right )$

$\equiv r\wedge \sim r\; \; \left ( let\, p\wedge \sim q\equiv r \right )$

$\equiv f$

Concepts used:

p→q = ∼p v q
Associative law: (p v q) v r = (p v r) v q
De morgan’s law: ∼(p ∧ q) = ∼p v ∼q

Q-6: (JEE Main - 2020)

The contrapositive of the statement: 'If a function is differentiable at a, then it is also continuous at “a” is:

If function 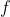is continuous at a, then it is not differentiable at a.
If function 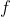is not continuous at a, then it is not differentiable at a.
If function 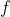is not continuous at a, then it is differentiable at a.
If function 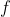is continuous at a, then it is differentiable at a.

Solution:

p = function is differentiable at a

q = function is continuous at a

contrapositive of statements p → q is

$\sim \mathrm{q} \rightarrow \sim \mathrm{p}$

Hence option (b): ‘If function is not continuous at a, then it is not differentiable at a.’ Is correct.

Having an understanding of mathematical reasoning helps in making Truth Tables. After getting the command in creating the truth table, Venn diagram, and important formulas, students will be able to score well in the examination.

Articles

DPUE Karnataka 2nd PUC Result 2026 Expected Date Live: Check Details Here

Apr 06, 2026

AP SSC Hall Ticket 2026 Out - Download 10th Class Hall Ticket @bse.ap.gov.in

Apr 06, 2026

CM SHRI Schools Admission Form 2026-27: Admit Card (April 8), Test Date (April 13), Result

Apr 06, 2026

AP 10th Class Exam Pattern 2026 | BSEAP SSC Subject-wise Marks Distribution & Question Paper Scheme

Apr 06, 2026