Volume And Capacity In Real-Life Containers: CBSE Class 8 Mensuration

Mathematics is not just a subject confined to textbooks and classrooms; it's a set of tools that help us understand and navigate the world around us. One such important tool is mensuration, which deals with the measurement of various geometric properties such as area, perimeter, volume, and capacity. In this article, we'll dive into understating volume and capacity, specifically focusing on real-life containers, as covered in the CBSE Class 8th Mensuration syllabus.

Menstruation is not just theoretical; it's a skill with real-world applications. Many competitive exams, including maths Olympiads and science fairs, require a strong grasp of these concepts. Solving practical problems involving volume and capacity can earn you extra points and recognition.

Understanding mensuration, especially volume, and capacity, is crucial for excelling in your Class 8th board exams. This article breaks down complex concepts into simple language, making it easier for you to understand. Step-by-step solved problems with real-life examples illustrate how to apply these concepts effectively.

Understanding Volume And Capacity

Volume is the measure of how much space an object occupies, while capacity refers to the maximum amount that a container can hold. Imagine filling a water bottle or a box with objects - the space occupied or the amount held corresponds to their volume or capacity, respectively.

Concepts Discussed In CBSE Class 8 Mensuration

In the CBSE Class 8th Mensuration chapter, you'll encounter various key concepts such as

A Recap of Fundamental Geometric Concepts

Points: These are the building blocks of geometry, entities with no dimensions, often represented as dots.

Lines: One-dimensional entities that stretch infinitely in both directions, forming the basis for paths and connections.

Angles: These are formed when two lines intersect, creating spaces between them. They are essential for understanding shapes' orientations.

Polygons: Closed figures with straight sides and vertices, encompassing an array of shapes like triangles, quadrilaterals, pentagons, and hexagons.

Calculating the Area of a Trapezium

A trapezium is a four-sided polygon with one pair of parallel sides.

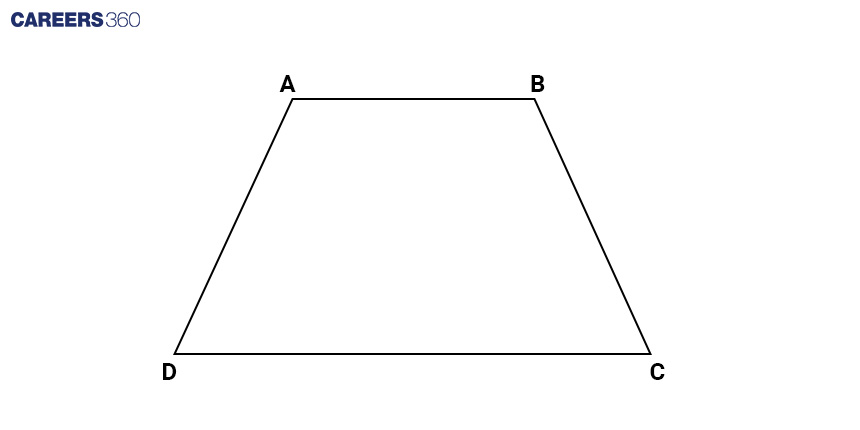
To calculate its area, we employ a straightforward formula:

Area = 1/2(Sum of Parallel Sides) Height

Here, the height represents the perpendicular distance between the parallel sides. This formula ingeniously calculates the average length of the parallel sides and multiplies it by the height, effectively determining the trapezium's area.

Unveiling the Area of a General Quadrilateral

When dealing with a quadrilateral that is not a trapezium, we need to dissect it into triangles to determine its area. This is done by finding the midpoints of the diagonals, effectively dividing the shape into four triangles.

The formula for calculating the area of a general quadrilateral is derived from this principle of triangulation.

Area Calculation for Polygons

For regular polygons—shapes with congruent sides and angles—the area can be determined using the formula:

Area = (1/2)Apothem Perimeter

Area = (1/2) (Apothem)(n)(Side)

The apothem refers to the distance from the centre of the polygon to a side. By combining the concepts of the shape's centre and its perimeter, we can accurately compute the area.

Exploring Three-Dimensional Solid Shapes

Moving beyond the realm of 2D shapes, we encounter solid shapes, objects with length, width, and height. These shapes—such as cubes, cuboids, cylinders, spheres, cones, and pyramids—possess distinct properties, including the number of faces, edges, and vertices they feature.

Surface Area and Volume

Calculating the surface area and volume of various solid shapes is another pivotal aspect of mensuration:

Surface Area: For a cube, it's simply six times the square of its side length. In the case of a cuboid, we sum up the areas of its six rectangular faces. The surface area of a cylinder involves adding the areas of its two circular bases and its lateral surface, essentially a wrapped-around rectangle.

Volume: The volume of a cube involves cubing its side length. For a cuboid, it's the product of its length, width, and height. The volume of a cylinder is determined by multiplying the base area (circle) by the height.

Volume and Capacity

Volume and capacity, often used interchangeably, are distinct concepts. Volume pertains to the measure of space occupied by a solid object, while capacity refers to the maximum amount of liquid a container can hold. While closely related, volume applies to all three-dimensional objects, not just containers.

Also check - NDA vs. JEE: A Comprehensive Comparison For A Bright Future

Volume And Capacity Derivation of Different Solids

Cubes

The volume of a cube can be determined through various formulas that correspond to the provided information. The calculation depends on either the given side length or the measurement of the cube's diagonal.

When the side length (s) of the cube is known, its volume (V) is calculated as V = s³.This can be shown below image

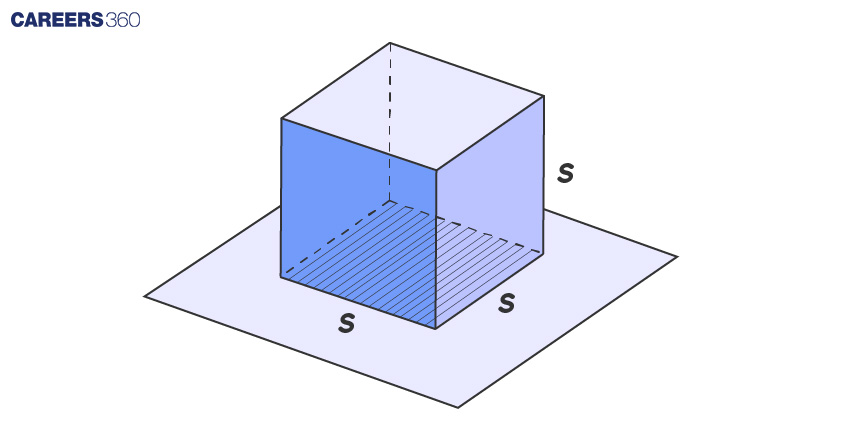
Alternatively, if the cube's diagonal (d) is given, the volume (V) can be computed using the formula V = (√3 × d3) / 9. This can be shown in the below image.

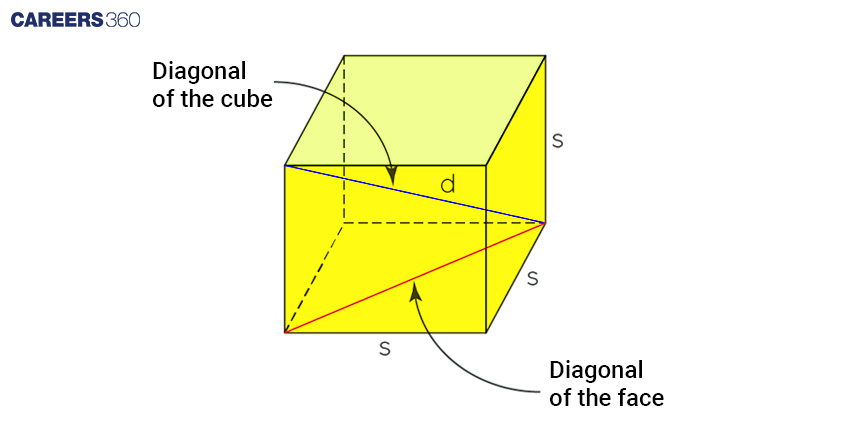
We diagonal of a face using Pythagoras formula

Face diagonal = √(Side²+Side²)

Face diagonal = √2 s

Diagonal of cube = √[(diagonal of face)²+side²]

Diagonal of cube =d = √3 s

V = s³ = (d/√3)³ = (√3 d³)/9

Cylinders

Imagine a cylinder like a can or a straw. It's a bit like a box, but the sides are curved. Now, even though a cylinder is not exactly like a box (we call it a prism), we can still use the same maths to find out how much stuff can fit inside it.

Here's the simple formula for the volume of a cylinder:

Volume = (Area of the base)(Height)

The "base" is the bottom part of the cylinder, like the bottom of a can. And the "height" is how tall the cylinder is, like the height of the can.

Now, let's look at different types of cylinders and their volume formulas:

Right Circular Cylinder: This is like a normal can or a glass. The formula for its volume is: Volume = π (radius²) height
Here, "radius" is the distance from the centre to the edge of the circle at the bottom.

Oblique Cylinder: If the cylinder isn't standing up straight, it's oblique. But guess what? We still use the same formula as the right circular one!

Elliptic Cylinder: Imagine a can that's squashed or stretched. The formula for its volume is: Volume = π (radius₁)(radius₂)(height)
Here, "radius1" and "radius2" are the distances from the centre to the edges of the oval base.

Right Circular Hollow Cylinder: This is like a pipe, with a hole in the middle. The formula for its volume is a bit different:

Volume = π (Outer Radius² - Inner Radius²) (height)
Here, "Outer Radius" is the distance from the centre to the outer edge of the pipe, and "Inner Radius" is the distance to the inner edge.

All of the above different types of cylinders can be visualised using the below image.

Cones:

Think of an ice cream cone. Its volume, or how much ice cream it can hold, can be found using a simple maths trick.

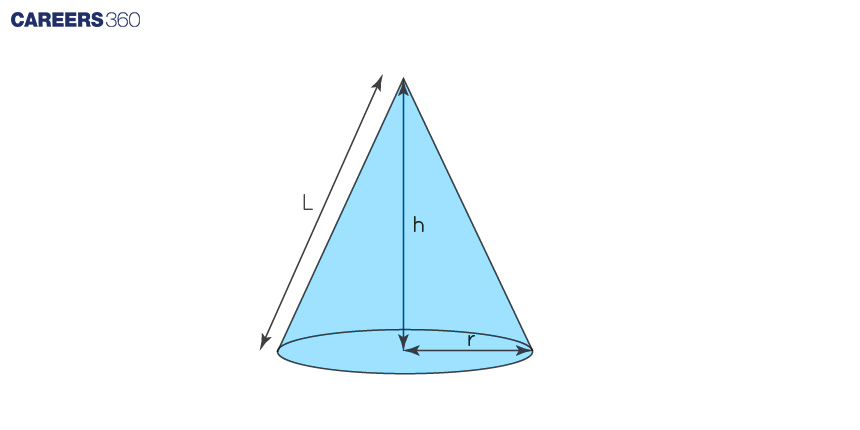
Imagine the bottom of the cone is a circle. The volume of the cone is like taking one-third of that circle and stretching it up to the tip of the cone.

Here's the easy formula for the volume of a cone:

Volume = (1/3) π (radius²)(height)

The "radius" is the distance from the centre of the circle at the bottom to its edge. And the "height" is how tall the cone is, from the tip to the bottom centre.

Volume in the format of slant height

L = √(r² + h²)

h = √(L² - r²)

Volume = (1/3) π r² (L² - r²)

Solved Problems

Problem 1:

Finding the Volume of a Cylinder Sam has a cylindrical water tank with a height of 50 cm and a base radius of 10 cm. He wants to know how much water the tank can hold. Help him find the volume of the cylinder.

Solution:

Given: Height (h) = 50 cm, Radius (r) = 10 cm

We know the formula for the volume of a cylinder is V = πr2h.

Substitute the values

Volume (V) = π (10 cm)² (50 cm)

Volume (V) = π (100 cm²)(50 cm)

Volume (V) = 5000π cm³

So, the cylinder can hold approximately 5000π cubic centimetres of water.

Problem 2:

Volume of a Cone Raju wants to make a party hat for her teddy bear. She has a cone-shaped piece of paper with a radius of 6 cm and a height of 12 cm. How much paper does he need to make the hat?

Solution:

Given: Radius (r) = 6 cm, Height (h) = 12 cm

The formula for the volume of a cone is V = (1/3)πr²h.

Substitute the values:

Volume (V) = (1/3)π (6 cm)²(12 cm)

Volume (V) = (1/3)π (36 cm²)(12 cm)

Volume (V) = 432π cm³

So, Raju needs approximately 432π square centimetres of paper to make the party hat for her teddy bear.

Also check - CBSE Class 10: How Quadratic Equations Can Help You Make A Shot In Basketball

Hope you now have a clear idea about volume and capacity and other concepts that are discussed in the Class 8 chapter on Mensuration. This will help you not only in competitive exams but also in understanding world events.