Master The Art Of Problem-Solving With Linear Equations

Mathematics, often considered a challenging subject, possesses an inherent beauty and practicality that can be unlocked through a sincere study of linear equations. As students progress in their educational journey, they encounter various mathematical concepts that bridge the gap between abstract theory and real-life application. Linear equations, a fundamental element of algebra, serves as an excellent example.

Linear equations appear in your exams, both the ones in school and competitive tests like JEE, NEET, and Olympiads. Learning how to handle these equations isn't just about passing exams; it's about gaining problem-solving skills. In this comprehensive exploration, we will discuss linear equations, focusing on the curriculum taught in Class 8, and discover how these seemingly complex mathematical tools are invaluable for solving real-life problems.

Understanding The Basics Of Linear Equations

Linear equations might sound intimidating at first, but they are essentially mathematical sentences that describe a relationship between two or more variables. In their simplest form, they look like this:

ax + b = c

where

a, b, and c are numbers, and x is the variable we're trying to find. These equations help us solve various real-world problems by finding the value of x.

Let's consider a straightforward example: You go to a store to buy some pens, and each pen costs 5 ₹. If you buy x pens and spend 20 ₹, how many pens did you buy? This situation can be represented by a linear equation: 5x = 20. To solve it, you simply need to figure out what value of x makes the equation true. In this case, x equals 4, which means you bought 4 pens.

Applications In Everyday Life

Here are some common scenarios where linear equations come into play in our daily lives:

Also Read | Discover the Science of Cooking: How Heat and Energy Help In Preparing Food

Financial Planning

Suppose you're saving up for a new bicycle, and you want to know how many weeks it will take to reach your savings goal. If you save 1,000 ₹ per week and need 12,000 ₹ for the bike, you can use a linear equation to find out how many weeks it will take: 1,000x = 12,000. Solving for x tells you that it will take 12 weeks to save enough money.

Distance, Time, and Speed

Linear equations can help you calculate how long it will take to reach a destination based on your speed and the distance you need to travel. For example, if you're driving at a constant speed of 60 kilometres per hour and you want to know how long it will take to cover 240 kilometres, you can use the equation 60x = 240. Solving for x reveals that it will take 4 hours.

Mixing Solutions

In chemistry or cooking, you might need to mix two solutions of different concentrations to achieve the desired concentration. Linear equations can help you calculate the amounts of each solution needed. For instance, if you have a 10 per cent sugar solution and want to make 500 ml of a 20 per cent sugar solution, you can set up linear equations and solve for variables.

Growth and Trends

Linear equations can also be used to analyse trends and make predictions. For instance, if you're tracking the growth of a plant over time and know that it grew two inches every week, you can use a linear equation to predict its height in the future.

These examples demonstrate how linear equations serve as powerful problem-solving tools in various aspects of our daily lives, from managing finances to planning travel and even creating delicious recipes.

Solving Linear Equations: Step-By-Step Approach

Now that we've seen how linear equations are used in real life, let's dive into the step-by-step process of solving them.

Step 1: Simplify Both Sides of the Equation

Begin by simplifying both sides of the equation. This might involve combining like terms, distributing numbers, or performing other basic operations to make the equation more manageable.

Step 2: Get the Variable on One Side

Your goal is to get all terms containing the variable x on one side of the equation and the constants on the other. You can achieve this by adding or subtracting the same value from both sides. For example, if you have 2x + 3 = 7, you can subtract 3 from both sides to isolate 2x on one side: 2x = 4.

Step 3: Isolate the Variable

To get x by itself, divide both sides of the equation by the coefficient of x. In our example, you'd divide both sides by 2: 2x/2 = 4/2, which simplifies to x = 2.

Step 4: Check Your Solution

Always double-check your solution by plugging the value you found for x back into the original equation to ensure it's correct.

Let's practise these steps with a few examples:

Example 1: Solve for x in the equation 2(x + 4) = 18.

Step 1: Simplify both sides: 2(x + 4) = 18.

Step 2: Distribute the 2 on the left side: 2x + 8 = 18.

Step 3: Get the variable on one side: Subtract 8 from both sides: 2x = 10.

Step 4: Isolate the variable: Divide both sides by 2: 2x/2 = 10/2, which simplifies to x = 5.

Also Check - Triangles And Parallelograms In Carpentry: A Fusion Of Mathematics And Craftsmanship In Class 9

Graphical Representation Of Linear Equations

Another valuable aspect of understanding linear equations is their graphical representation. Linear equations can be depicted as straight-line graphs, making it easier to visualise and analyse their behaviour. Let's explore how this graphical representation works:

Consider the linear equation y = 2x + 3. This equation describes a straight line on a graph, where y depends on the value of x. To create a graph for this equation, follow these steps:

Step 1: Choose a range of values for x, such as -2, -1, 0, 1, 2, and 3.

Step 2: Calculate the corresponding values for y using the equation y = 2x + 3. For example, when x = −2,

y = 2(−2) + 3 = −1.

Step 3: Plot the points

(−2,−1), (−1,1), (0,3), (1,5), (2,7), and (3,9) on a graph.

Step 4: Connect the points with a straight line. This line represents the graph of the equation y = 2x + 3.

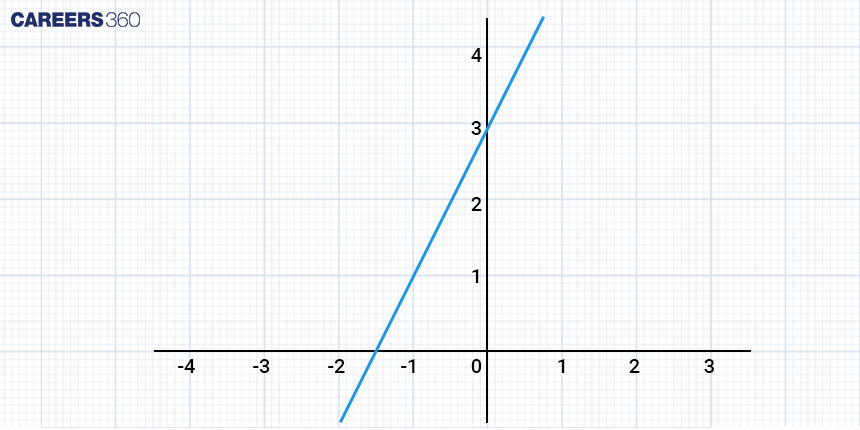
Now, you have a visual representation of the relationship between x and y described by the linear equation. This graphical approach can help you understand how changing the value of x affects y and vice versa.

Additionally, graphs can be used to solve systems of linear equations. When you have two or more linear equations, you can represent them as lines on a graph. The point where these lines intersect is the solution to the system of equations. This graphical method provides a visual way to find the solution and is particularly useful for understanding how different equations relate to each other.

Systems of Linear Equations

While we've primarily focused on solving single linear equations, it's essential to understand systems of linear equations. These systems involve multiple equations with the same variables, and the goal is to find values that satisfy all the equations simultaneously.

Let's consider a simple example:

Problem: You have ₹500 to spend on buying apples and bananas. Apples cost ₹40 each, and bananas cost ₹10 each. You want to buy a total of 20 fruits. How many apples and how many bananas should you buy?

To solve this problem, we can set up a system of linear equations:

Equation 1: x + y = 20 (where ‘x’ is the number of apples and ‘y’ is the number of bananas)

Equation 2: 40x + 10y = 500 (since apples cost ₹40 each and bananas cost ₹10 each)

Now, we have a system of two linear equations with two variables (a and b). To find the values of x and y that satisfy both equations, we can use methods like substitution or elimination.

Upon solving, you'll find that

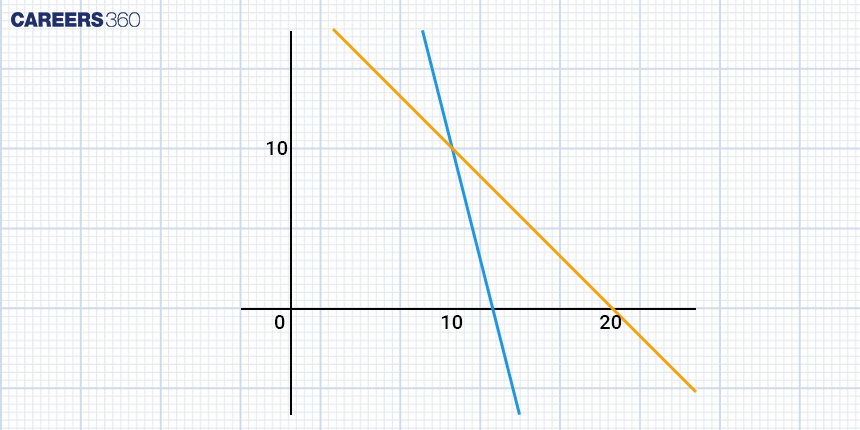
x = 10 (10 apples) and y = 10 (10 bananas). This means you should buy 10 apples and 10 bananas to stay within your budget and reach your desired total of 20 fruits.

Systems of linear equations are powerful tools for solving complex real-life problems that involve multiple conditions or constraints.

Also Check - How Does Early Onset Of Puberty Affect Individuals Over Time?

Applications In Science And Economics

Linear equations are not limited to mathematics classes; they have broad applications in various scientific and economic disciplines. Let's explore how they are used in these fields:

>>Physics: In physics, linear equations are used to model and analyse various phenomena. For instance, they describe the relationship between force (F), mass (m), and acceleration (a) in Newton's second law of motion, F = ma. This equation helps physicists understand how objects move and interact with each other.

>>Economics: Linear equations play a vital role in economics, particularly in the analysis of supply and demand. Equations like

P = a − bQ represents demand curves, where P is the price of a product, Q is the quantity demanded, and a and b are constants. These equations help economists predict how changes in price and quantity affect market behaviour.

>>Engineering: Engineers rely on linear equations to design and analyse systems and structures. For example, in electrical engineering, Ohm's law (V = IR) represents the relationship between voltage (V), current (I), and resistance (R) in an electrical circuit. Engineers use this equation to design circuits and troubleshoot electrical problems.

Challenges and Advanced Topics

As students progress through their mathematical journey, they may encounter more complex linear equations and related topics. While the class 8th curriculum primarily focuses on foundational concepts, it's beneficial to have a glimpse of what lies ahead. Here are a few advanced topics related to linear equations:

Systems of Linear Equations with Three Variables

In addition to systems with two variables, students will encounter systems with three variables. These systems involve three equations and three unknowns, requiring more advanced methods for solving.

Matrices and Determinants

Matrices are arrays of numbers used to represent linear equations compactly. Determinants, derived from matrices, play a crucial role in solving systems of linear equations and have applications in various mathematical and scientific fields.

Linear Programming

Linear programming is a mathematical technique used to optimise solutions to real-world problems. It involves maximising or minimising a linear objective function subject to linear constraints, making it a valuable tool in operations research, economics, and engineering.

Nonlinear Equations

While linear equations describe relationships with a constant rate of change, nonlinear equations involve more complex relationships. These equations can be graphed as curves rather than straight lines and are encountered in fields like calculus and physics.