Chemical Kinetics: Mathematical Modeling Of Reaction Rates

Chemistry is a fascinating subject that explores the composition, properties, and transformations of matter. As a Class 12 student, you may be wondering how mathematics plays a role in understanding chemical reactions. Well, in the realm of chemical kinetics, mathematics becomes a powerful tool to describe and predict the rates at which reactions occur.

Also check - Mathematics Of Optics: Understanding Light And Its Interactions With Matter

Let’s take a deeper look and understand how?

Fundamentals Of Chemical Kinetics

Chemical kinetics focuses on the study of reaction rates and the factors that influence them. It seeks to understand how and why chemical reactions occur at different speeds. Following are the fundamentals of chemical kinetics that give insights into the dynamics of reactions and make predictions about their behaviour.

Reaction Rate

The reaction rate refers to the speed at which a chemical reaction takes place. It is determined by how quickly the reactants are converted into products or how rapidly the product concentration increases. Reaction rates are typically expressed in terms of moles per unit time (e.g., mol/L/s).

Factors Influencing Reaction Rates

Several factors can influence the rate of a chemical reaction:

• Nature of Reactants: Different substances react at different rates due to variations in their chemical properties and molecular structures.

• Concentration of Reactants: Increasing the concentration of reactants generally leads to a higher reaction rate. This is because a higher concentration provides more reactant particles, increasing the frequency of collisions and, therefore, the likelihood of successful collisions.

• Temperature: Raising the temperature generally accelerates reaction rates. This is because higher temperatures increase the kinetic energy of molecules, resulting in more energetic collisions and a greater number of successful collisions.

• Surface Area: In reactions involving solids, increasing the surface area by grinding or subdividing the solid leads to a higher reaction rate. This is because a greater surface area provides more exposed particles, allowing for increased contact and faster reaction rates.

• Catalysts: Catalysts are substances that speed up reactions without being consumed in the process. They work by providing an alternative reaction pathway with lower activation energy, thus lowering the energy barrier for the reaction to occur. Catalysts can significantly increase reaction rates.

Rate Law

The rate law or rate equation is a mathematical expression that relates the rate of a reaction to the concentrations of the reactants. The general form of a rate law is:

Rate = k[A]^m[B]ⁿ

Here, [A] and [B] represent the concentrations of the reactants A and B, respectively. The exponents m and n are the reaction orders for reactants A and B, respectively. The reaction orders determine how changes in reactant concentrations affect the reaction rate.

The constant k is the rate constant, which incorporates the effects of temperature and the specific reaction mechanism. The rate constant remains constant at a given temperature and provides information about the speed of the reaction. Determining the rate law and rate constant requires experimental data, where the reaction rate is measured at different reactant concentrations.

Reaction Mechanism

The reaction mechanism describes the step-by-step sequence of elementary reactions that occur during a complex reaction. It explains how reactant molecules rearrange and bond to form products. Each step in the mechanism has its own rate equation, and the slowest step, known as the rate-determining step, determines the overall rate of the reaction. Understanding the reaction mechanism is essential in chemical kinetics, as it provides insights into the sequence of events that lead to product formation.

Activation Energy

Activation energy (Ea) is the minimum amount of energy required for a reaction to occur. Molecules must possess this energy to overcome the energy barrier and initiate the reaction. The Arrhenius equation relates the rate constant (k) to the temperature (T) and activation energy (Ea).

Higher activation energies generally correspond to slower reaction rates, as fewer molecules possess sufficient energy to overcome the barrier.

Reaction Order

The reaction order for a particular reactant indicates how the concentration of that reactant affects the rate of the reaction. It can be determined experimentally and may be zero, first, second, or even fractional. The sum of the reaction orders for all reactants in the rate law gives the overall reaction order.

Mathematics Behind Different Types Of Reactions

There are different types of reactions, and the rate law for each type depends on the order of the reaction.

Zero-Order Reaction

In a zero-order reaction, the rate of the reaction is independent of the concentration of the reactants. The rate law for a zero-order reaction is given by the equation:

Rate = k

Where:

• Rate is the rate of the reaction
• k is the rate constant

Example: Consider the decomposition of a substance A, where A → products. If the reaction is zero-order with respect to A, the rate law would be written as:

Rate = k

Mathematical Calculation: To determine the concentration-time relationship for a zero-order reaction, you can integrate the rate law. Let's assume the initial concentration of A is [A]0, and after a time t, the concentration of A is [A].

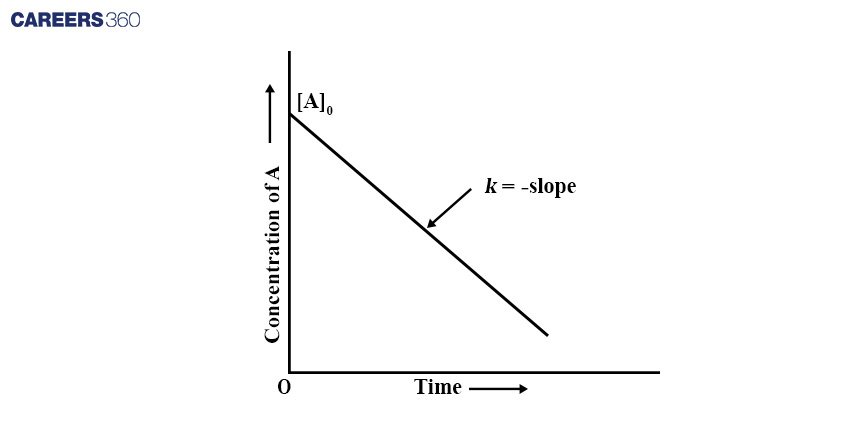
[A] - [A]₀ = -kt

Where:

• [A] is the concentration of A at time t
• [A]0 is the initial concentration of A
• k is the rate constant

First-Order Reaction

In a first-order reaction, the rate of the reaction is directly proportional to the concentration of a single reactant. The rate law for a first-order reaction is given by the equation:

Rate = k[A]

Example: Consider the decomposition of a substance A, where A → products. If the reaction is first order with respect to A, the rate law would be written as:

Rate = k[A]

Mathematical Calculation: Similar to the zero-order reaction, you can integrate the rate law to determine the concentration-time relationship for a first-order reaction. Assuming [A]0 is the initial concentration of A and [A] is the concentration of A at time t, the equation becomes:

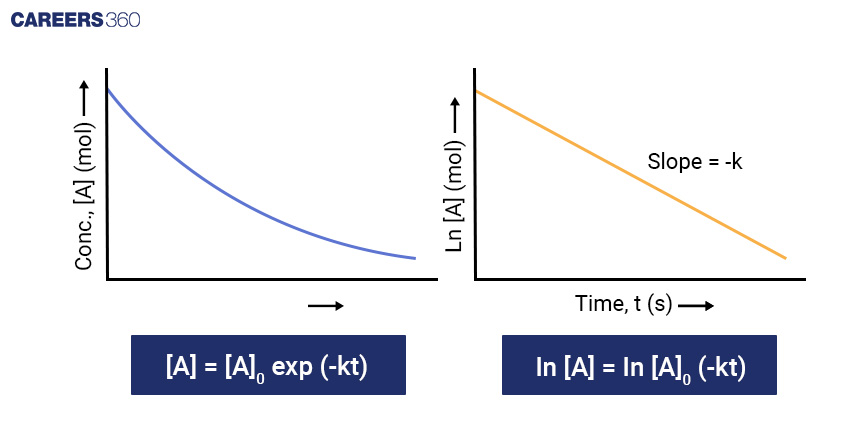
[A] = [A]₀ e^(-kt)

Taking natural log both side

ln[A] = ln[A]₀ - kt

Where:

• ln is the natural logarithm
• [A] is the concentration of A at time t
• [A]0 is the initial concentration of A
• k is the rate constant

Q-1. A first-order reaction where the rate constant (k) is 0.05 min⁻¹, and the initial concentration of the reactant (A) is 2.0 M. We want to determine the concentration of A after 10 minutes.

Solution:

To solve this, we can use the first-order rate law equation:

Rate = k[A]

Rearranging the equation, we have:

[A] = Rate / k

Given that Rate= -d[A]/dt (negative sign indicates the decrease in concentration),

d[A]/[A] = -kdt

Integrating both side for time 0 to t. In this time interval let's consider concentration change [A]₀ to [A]

∫d[A]/[A] = -∫kdt

ln[A]/[A]₀ = -kt

Where: [A]₀ is the initial concentration of A, [A] is the concentration of A at time t, k is the rate constant, t is the time.

Now, let's substitute the given values into the equation:

ln{[A]/2.0} = -(0.05 min-1)(10 min)

Solving for [A]:

ln{[A]/2.0} = -(0.5)

[A]/2.0 = e^(-0.5)

[A] = 2.0 e^(-0.5)

Using a calculator, we find that [A] ≈ 1.37 M after 10 minutes.

Second-Order Reaction

In a second-order reaction, the rate of the reaction is proportional to the square of the concentration of a single reactant or the product of the concentrations of two reactants. The rate law for a second-order reaction can take different forms:

a) Rate = k[A]²

b) Rate = k[A][B]

Example: Consider the reaction 2A → products. If the reaction is second order with respect to A, the rate law would be written as:

Rate = k[A]²

Mathematical Calculation: To determine the concentration-time relationship for a second-order reaction, you can use integrated rate laws similar to the first-order reaction.

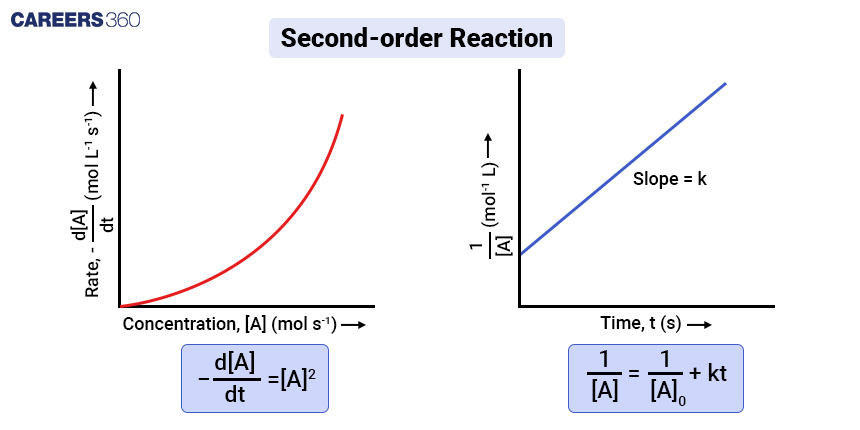
Assuming [A]₀ is the initial concentration of A and [A] is the concentration of A at time t, the equation becomes:

-d[A]/dt = k[A]²

Rearranging the equation

d[A]/[A]² = -kdt

Integrating both side for time 0 to t. In this time interval concentration change from [A]₀ to [A]

∫d[A]/[A]² = -∫kdt

1/[A] = 1/[A]₀ + kt

Where:

• [A] is the concentration of A at time t
• [A]₀ is the initial concentration of A
• k is the rate constant

Q-1. A second-order reaction with respect to A, where the rate constant (k) is 0.02 M⁻¹ min⁻¹ and the initial concentration of A is 0.5 M. We want to determine the time required for the concentration of A to decrease to 0.1 M.

Solution:

The rate law for this reaction is:

Rate = k[A]²

We know

1/[A] = 1/[A]₀ + kt

Given,

[A]₀ = 0.5 M, [A] = 0.1 M, k = 0.02 M^(-1)Min^(-1)

Putting all the values in equation

10/0.1 = 1/0.5 + (0.02)t

Simplifying:

10 = 2 + (0.02)t

t = 8/0.02 = 400 min

Therefore, it would take approximately 400 minutes for the concentration of A to decrease from 0.5 M to 0.1 M in this second-order reaction.

Also check - Class 12 Biology: Biotech Innovations And Ethical Issues

Now, You have a basic idea of how mathematical calculations and concepts play a crucial role in understanding the kinetics and behaviour of chemical reactions.