RD Sharma Class 12 Exercise 13.1 Differentials, Errors and Approximations Solutions Maths

RD Sharma Class 12 Exercise 13.1 Differentials, Errors and Approxim Solutions Maths - Download PDF Free Online

Edited By Kuldeep Maurya | Updated on Jan 27, 2022 10:00 AM IST

The class 12 mathematics syllabus is vast and pretty difficult to finish. Students in class 12 suffer a lot because there is not enough time to clear their doubts in school and to make sure they have understood the concepts properly. Therefore, students are recommended to use RD Sharma class 12th exercise 13.1 solutions for their home practice as it would help them improve their performance. The 13th chapter of the NCERT Mathematics Textbook is titled Differentials, Errors, and Approximations. This section will explore concepts like Absolute error, Relative error, Percentage error, Geometrical meaning of differentials, etc. The RD Sharma Solutions contains 10 questions based on the entire chapter.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics

This Story also Contains

RD Sharma Class 12 Solutions Chapter 13 Differentials, Errors and Approximations - Other Exercise
Differentials, Errors and Approximations Excercise: 13.1
RD Sharma Chapter wise Solutions

RD Sharma Class 12 Solutions Chapter 13 Differentials, Errors and Approximations - Other Exercise

Differentials, Errors and Approximations Excercise: 13.1

Differentials, errors and approximations exercise 13.1 question 1

Answer: $\Delta y=0-$ No change

Given: $y=sinx$ and $x$ changes from $\frac{\pi }{2}$ to $\frac{22}{14}$
Solution: Suppose $\chi=\frac{\pi}{2}$ Therefore $x+\Delta x=\frac{22}{14}$
$\begin{aligned} &\rightarrow \frac{\pi}{2}+\Delta x=\frac{22}{14} \\\\ &\Delta x=\frac{22}{14}-\frac{\pi}{2} \end{aligned}$

→ Differentiate y with respect to x

$\frac{d y}{d x}=\cos x$
⇒ As we know that $(\sin x)=\cos x$
$\therefore \frac{d y}{d x}=\cos x$
⇒ when, $x=\frac{\pi}{2}$ we have $\frac{d y}{d x}=\cos \left(\frac{\pi}{2}\right)$
$\begin{aligned} &\Rightarrow\left(\frac{d y}{d x}\right) x=\frac{\pi}{2}=0 \\\\ &\Rightarrow \Delta y=\left(\frac{d y}{d x}\right) \Delta x \end{aligned}$

Here $\frac{d y}{d x}=0$ and $\Delta x=\frac{22}{14}-\frac{\pi}{2}$

$\Delta y=(0)\left(\frac{22}{14}\right)-\left(\frac{\pi}{2}\right)$

$\Delta y=(0)\$

Differentials, errors and approximations exercise 13.1 question 2

Answer: decrease $80\pi \; cm^{2}$
Hint: As we know, volume of a sphere of radius $x$ is given by $v=\left(\frac{4}{3}\right) \pi x^{3}$
Given: the radius of a sphere changes from 10cm to 9.8cm
Solution: Suppose $x$ be the radius of the sphere and $\Delta x$ be the change in the value of $x$
$\Rightarrow$ Thus, we have $x=10$ and $x+ \Delta x=9.8$ $\begin{aligned} &\Rightarrow 10+\Delta x=9.8 \\\\ &\Delta x=9.8-10 \\\\ &=-0.2 \end{aligned}$

⇒ Differentiate $v$ with respect to $x$

$\begin{aligned} &\frac{d v}{d x}=\frac{d}{d x}\left(\left(\frac{4}{3}\right) \pi x^{3}\right) \\\\ &\frac{d v}{d x}=\frac{4 \pi}{3} \frac{d}{d x}\left(x^{3}\right) \\\\ &\frac{d}{d x}\left(x^{3}\right)=n x^{n-1} \end{aligned}$

$\begin{aligned} &\frac{d v}{d x}=4 \pi x^{2} \text { when } \frac{d v}{d x}=4 \pi \times 100=400 \\\\ &(x=10) \\\\ &\Rightarrow \Delta y=\left(\frac{d y}{d x}\right) \Delta y \end{aligned}$

$\begin{aligned} &\frac{d v}{d x}=400 \pi \text { and } \Delta x=-0.2 \\\\ &\Delta x=(400 \pi)(-0.2)=-80 \pi \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 3

Answer: $2 k \pi c m^{2}$
Hint: Here, Area of a circular plate of radius $x$ is given by $A=\pi x^{2}$
Given: the radius of a circular plate initially is 10 cm and it increase by K%
Solution: Suppose $x$ be the radius of the plate, and $\Delta x$ is the change in the value of $x$
Thus we have $x=10 \text { and } \Delta x=\frac{K}{100} \times 10$
So, $\Delta x=0.1 K$
Differentiating A with respect to $x$
$\begin{aligned} &\frac{d A}{d x}=\frac{d}{d x}\left(\pi x^{2}\right) \\\\ &\frac{d A}{d x}=\pi \frac{d}{d x}\left(x^{2}\right)=n x^{n-1} \\\\ &\Rightarrow \frac{d A}{d x}=2 \pi x \end{aligned}$
$\begin{aligned} &\Rightarrow \text { when } x=10 \text { and } \frac{d A}{d x}=2 \pi(10) \text { so, } \frac{d A}{d x}=20 \pi \\\\ &\Rightarrow \Delta y=\frac{d y}{d x} \Delta x \end{aligned}$
$\begin{aligned} &\text { Here, } \frac{d A}{d x}=20 \pi \text { and } \Delta x=0.1 K \\\\ &\Delta A=(20 \pi)(0.1 K) \\\\ &\Delta A=2 K \pi \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 4

Answer: 2% Error
Hint: area of a cubical box of radius $x$ is given by $s=6 x^{2}$
Given: $\Delta x$ is the error in the value of $x \; \; \Delta x=0.01 x$
Solution: suppose $x$ be the of cubical box
So, $\Delta x=0.01 x$
Differentiate $s$ with respect to $x$
$\begin{aligned} &\frac{d s}{d x}=\frac{d}{d x}\left(6 x^{2}\right) \\\\ &\Rightarrow \frac{d s}{d x}=6 \times \frac{d}{d x}\left(x^{2}\right) \\\\ &\frac{d}{d x}\left(x^{n}\right)=n x^{n-1} \Rightarrow \frac{d s}{d x}=6 x 2 x=12 x \end{aligned}$
⇒ As we know that if $y=F(x) \Delta x$ is a small increment in $x$ , then the corresponding increment in $y$
$\Delta x=F(x+\Delta y)-F(x)$ , is approximately given as $\Delta y=\left(\frac{d y}{d x}\right) \Delta x$
$\begin{aligned} &\Rightarrow \text { Here, } \frac{d s}{d x}=12 x \Delta x=0.01 x \\\\ &\Delta s=12 x \times 0.01 x \\\\ &\Delta s=0.12 x^{2} \end{aligned}$
$\Rightarrow$ Percentage of error is
$\text { Error }=\frac{0.12 x^{2}}{6 x^{2}} \times 100 \%=0.02 \times 100 \%=2 \%$

Differentials, errors and approximations exercise 13.1 question 5

Answer: 0.3%
Hint: Surface volume of a sphere of radius $x$ is given by $v=\frac{4}{3} \pi x^{3}$
Given: let $x$ be the radius and $\Delta x$ be the error in the value $x$
Solution: Suppose $x$ be the radius of the sphere and $\Delta x$ be the error in the value $x$
⇒ Thus, we have $\Delta x=\left(\frac{0.1}{100}\right) \times(x)$
So, $\Delta x=0.001 x$
⇒ Volume of a sphere, $v=\frac{4}{3} \pi x^{3}$
So, Differentiate v with respect $x$
$\begin{aligned} &\Rightarrow \frac{d v}{d x}=\frac{d}{d x}\left(\frac{4}{3} \pi x^{3}\right) \Rightarrow \frac{d v}{d x}=\frac{4 \pi}{3} \frac{d}{d x}\left(x^{3}\right) \\\\ \\\\ &\Rightarrow \frac{d v}{d x}=\frac{4 \pi}{3}\left(4 x^{2}\right)=4 \pi x^{2} \end{aligned}$
$\Rightarrow$ As we know, $y=f(x)$ and $\Delta x$ is a smaller increment,
$\begin{aligned} &\Delta y=\left(\frac{d v}{d x}\right) \Delta x=0.001 x \\\\ &\Delta x=0.004 \pi x^{3} \\\\ &\text { Here, } \frac{d v}{d x}=4 \pi x^{2} \text { and } \Delta x=0.001 x \end{aligned}$

$\Rightarrow$ Percentage error $=\frac{0.004 \pi x^{3}}{\frac{4}{3} \pi x^{3}} \times 100=0.003 \times 100=0.3 \%$

Differentials, errors and approximations exercise 13.1 question 6

Answer: 0.7%

Hint: Here we use the basic concept of area and logarithm
Given: $pv^{1.4}$ =constant
Solution: Given as $pv^{1.4}$ =constant and the decrease in $v$ is $\frac{1}{2}%$
$\Rightarrow$ Thus, we have $\Delta v=\left(\frac{-1}{2}\right) 100 x v$
So, $\Delta v=-0.005 v$
$\Rightarrow$ Now, $pv^{1.4}$ =constant
taking log on both sides,
$\log \left(p v^{1.4}\right)=\log (\text { constant })$
$\Rightarrow$ Differentiate both sides with respect to v
$\begin{aligned} &\frac{d}{d p}(\log p) x \frac{d p}{d v}+\frac{d}{d v}(1.4 \log v)=0 \\\\ &\Rightarrow \frac{d}{d p}(\log p) x \frac{d p}{d v}+1.4 \frac{d}{d v}(\log v)=0 \end{aligned}$
$\begin{aligned} &\Rightarrow \frac{d}{d x}(\log x)=\frac{1}{x} \\\\ &\Rightarrow \frac{d}{d v}=\frac{-1.4}{v} P \end{aligned}$
$\begin{aligned} &\Delta p=\left(\frac{-1.4}{v} p\right)(-0.005 x) \\\\ &\Delta p=0.007 p \end{aligned}$
$\Rightarrow$ Percentage of error is
$\text { Error }=\frac{0.007 p}{p} \times 100=0.7 \%$

Differentials, errors and approximations exercise 13.1 question 7

Answer: 2k%
Hint: total surface area of the cone is given by $s=\pi r^{2}+\pi r l$
Given: $\Delta x=\left(\frac{k}{100}\right) \times(x)$
$\Delta x=0.01 k x$
Solution: Suppose $x$ be the height of the cone and $\Delta x$ be the change in the value of $x$
⇒ Thus we have $\Delta x=\left(\frac{k}{100}\right) \times x$
$\Delta x=0.01 k x$
⇒ suppose us assume that radius, the semi height and semi vertical angle of the come to be $r$ , 1 and respectively as shown

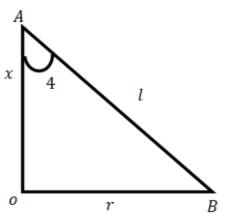
⇒ from above figure, using trigonometry

$\tan d=\frac{O B}{O A}=\frac{r}{x}$
⇒ we have also
$\cos x=\frac{O A}{A B}=\frac{x}{l}$
$1=\frac{x}{\cos x}$
⇒ Now the total surface area of the cone is given by
$s=\pi x^{2}+\pi r l$
⇒ from the above, we have $r=x \tan x \text { and } l=x \sec x$
$\Rightarrow s=\pi x^{2}+\pi(x \tan x \cdot x \sec x)$
⇒ Differentiate s with respect to $x$
$\begin{aligned} &\frac{d s}{d x}=\frac{d}{d x}\left[\pi x^{2} \tan x(\tan x+\sec x)\right] \\\\ &\Rightarrow \frac{d s}{d x}=\pi \tan x(\tan x+\sec x) \frac{1}{d x}\left(x^{2}\right) \end{aligned}$
$\begin{aligned} &\frac{d}{d x}\left(x^{n}\right)=n x^{n-1} \\\\ &\Rightarrow \frac{d s}{d x}=2 \pi x \tan x(\tan x+\sec x) \end{aligned}$
$\begin{aligned} &\Rightarrow \text { so, } \Delta x=\left(\frac{d y}{d x}\right) \Delta x \\\\ &\Rightarrow \text { Here } \frac{d s}{d x}=2 \pi x(\tan x+\sec x) \text { and } \Delta x=0.01 k x \\\\ &\Rightarrow \Delta s=(2 \pi x \tan (x)[\tan (x)+\sec (x)](0.01 k x) \end{aligned}$
⇒ Percentage of increase in S
$\begin{aligned} &\text { Increase }=\frac{\Delta s}{s} \times 100 y \\\\ &=100+\times 0 . .03 k \pi x^{2} \tan x[\tan x+\sec x] \\\\ &\pi x^{2} \tan x(\tan x+\sec x) \end{aligned}$
$\begin{aligned} &\text { Increase }=0.02 k \times 100 \\\\ &=2 k \% \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 8

Answer: 3k %
Hint: volume of a sphere of radius $x$ is given by $v=\frac{4}{3} \pi x^{3}$
Given: we have $\Delta x=0.01 k x$
Solution: Suppose the error in measuring the radius of a sphere be $k$
⇒ Suppose $x$ be the radius of the sphere and $\Delta x$ be the error in the value of $x$
⇒ Thus, we have $\Delta x=\left(\frac{k}{100}\right) \times(x)$
So, $\Delta x=0.01 k x$
⇒ Differentiate v with respect to $x$
$\begin{aligned} &\frac{d v}{d x}=\frac{d}{d x}\left(\frac{4}{3}\right) \pi x^{3} \\\\ &\Rightarrow \frac{d v}{d x}=\frac{4 \pi}{3} \frac{d}{d x}\left(x^{3}\right) \Rightarrow \frac{d}{d x}\left(x^{n}\right)=n x^{n-1} \end{aligned}$
$\begin{aligned} &\frac{d v}{d x}=\frac{4 \pi}{3}\left(3 x^{2}\right) \frac{d v}{d x}=4 \pi x^{2} \\\\ &\Rightarrow \Delta y=\frac{d y}{d x} \Delta x, \text { Here } \frac{d v}{d x}=4 \pi x^{2} \Delta x=0.01 k x \end{aligned}$
$\therefore \Delta x=0.04 k \pi x^{3}$
⇒ percentage of error is,
$\begin{aligned} &\text { Error }=\frac{0.04 k \pi x^{3}}{\frac{4}{3} \pi x^{3}} \times 100 \% \\\\ \end{aligned}$
$=\frac{0.04 k \pi x^{3}}{4 \pi x^{3}} \times 100 \times 3=3 k \%$

Differentials, errors and approximations exercise 13.1 question 9 (i)

Answer: 5.03
Hint: Here we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\sqrt{25.3}$
Solution: let $y=\sqrt{x}$
$\begin{aligned} &x=25 \& \Delta x=0.3 \\\\ &\Rightarrow \text { Since } y=\sqrt{x} \\\\ &\frac{d y}{d x}=\frac{d \sqrt{x}}{d x}=\frac{1}{2 \sqrt{x}} \end{aligned}$
⇒ Now,
$\begin{aligned} &\Delta y=\frac{d y}{d x} \Delta x \\\\ &=\frac{1}{2 \sqrt{x}} \times 0.3 \\\\ &=\frac{1}{2 \sqrt{x}} \times 0.3=0.03 \end{aligned}$
$\begin{aligned} &\Rightarrow \text { Also, } \Delta y= \frac{f(x+\Delta x)-f(x)}\ ={\sqrt{25+0.3}-\sqrt{25}} \\\\ &\sqrt{25.3}=5.03 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (ii)

Answer: 0.208
Hint: here we use the formula
Given: $(0.009)^{\frac{1}{3}}$
Solution: consider $y=x^{\frac{1}{3}} \text { Let } x=0.009 \text { and } \Delta x=0.001$ $\Delta x=(x+\Delta x)^{\frac{1}{3}}=(0.009)^{\frac{1}{3}}-(0.008)^{\frac{1}{3}}(0.009)^{\frac{1}{3}}=0.2+\Delta y$

⇒ Now, $dy$ is approximately equal to $\Delta y$ and is given by,

$\begin{aligned} &d y=\left(\frac{d y}{d x}\right) \Delta x=\frac{1}{3(x)^{\frac{2}{3}}}(\Delta x) \\\\ &=\frac{3}{3 \times 0.04}(0.001)=\frac{0.001}{0.12} \\\\ &=0.008 \end{aligned}$
Hence, the approximate value of $(0.004)^{\frac{1}{3}} i \text { is } 0.2+0.08=0.208$

Differentials, errors and approximations exercise 13.1 question 9 (iii)

Answer: 0.191667

Hint: Here we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $(0.007)^{\frac{1}{3}}$
Solution: consider the function $f(x)=3 \sqrt{x}$
Let:
$\begin{aligned} &x=0.008 \\\\ &x+\Delta x=0.007 \end{aligned}$
Then,
$\begin{aligned} &\Delta x=-0.001 \\\\ &\text { For } x=0.008, \end{aligned}$
$\begin{aligned} &y=\sqrt{0.008}=0.2 \\\\ &\text { Let, } d x=\Delta x=0.001 \\\\ &\text { Now } y=3 \sqrt{x} \end{aligned}$
$\begin{aligned} &\frac{d y}{d x}=\frac{1}{3(x)^{\frac{2}{3}}} \\\\ &\left(\frac{d y}{d x}\right) x=0.008=\frac{1}{0.12} \times 0.001=\frac{1}{120} \end{aligned}$ $\begin{aligned} &\Rightarrow \Delta y=\frac{1}{120}=0.008333 \\\\ &(0.007)^{\frac{1}{3}}=y+\Delta y=0.191667 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (iv)

Answer: 20.025
Hint: Here, we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\sqrt{401}$
Solution:
Let $y=x^{\frac{1}{2}}$
Where, $x=400$
$\begin{aligned} &x+\Delta x=401 \\\\ &\Delta x=1 \end{aligned}$
Now, $\frac{d y}{d x}=\frac{1}{2 \sqrt{x}}$
Using, $\Delta y=\frac{d y}{d x} \Delta x=\frac{1}{2 \sqrt{x}} \times 1$
Putting the value of $x$
$\begin{aligned} \sqrt{401} &=y+\Delta y \\\\ &=20+0.025 \\\\ &=20.025 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (v)
Answer: 1.96875

Hint : Here, we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $(15)^{\frac{1}{4}}$
Solution:
Let $y=x^{\frac{1}{4}}=(16)^{\frac{1}{4}}=2$
Where , $x=16$
$\begin{aligned} &x+\Delta x=15 \\\\ &\Delta x=-1 \end{aligned}$
Now, $y=x^{\frac{1}{4}}$
Differentiating w.r.t $x$
$\frac{d y}{d x}=\frac{1}{4} x^{\frac{-3}{4}}$
Using, $\Delta y=\frac{d y}{d x} \Delta x=\frac{1}{4 x^{\frac{3}{4}}} \times-1$
Putting the value of $x$
$\Delta y=\frac{-1}{4(16)^{\frac{3}{4}}}=\frac{-1}{4 \times 2^{3}}=-0.03125$
$\begin{aligned} (15)^{\frac{1}{4}} &=y+\Delta y \\\\ &=2+(-0.03125) \\\\ &=1.96875 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (vi)

Answer: 3.9961
Hint: Here, we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $(255)^{\frac{1}{4}}$
Solution:
Let $y=x^{\frac{1}{4}}=(256)^{\frac{1}{4}}=4$
where $x=16$
$\begin{aligned} &x+\Delta x=255 \\\\ &\Delta x=-1 \end{aligned}$
Now, $y=x^{\frac{1}{4}}$
Differentiating w.r.t $x$
$\frac{d y}{d x}=\frac{1}{4} x^{\frac{-3}{4}}$
Using,
$\Delta y=\frac{d y}{d x} \Delta x=\frac{1}{4 x^{\frac{3}{4}}} \times-1$
Putting the value of $x$
$\begin{aligned} &\Delta y=\frac{-1}{4(256)^{\frac{3}{4}}}=\frac{-1}{4 \times 4^{4 \times \frac{3}{4}}}=\frac{-1}{256}=-0.0039 \\\\ &(255)^{\frac{1}{4}}=y+\Delta y \end{aligned}$
$\begin{aligned} &=4+(-0.0039) \\\\ &=3.9961 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (vii)

Answer: 0.2495
Hint: Here, we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\frac{1}{(2.002)^{2}}$
Solution:
consider $y=\frac{1}{x^{2}}$
Here $x=2 \text { and } \Delta x=0.002$
On differentiating wrt $x$ ,
$\frac{d y}{d x}=\frac{-2}{x^{3}}$
So we get,
$\Delta y=\frac{d y}{d x} \cdot \Delta x$
On substituting the value we get,
$\Delta \mathrm{y}=\frac{-2}{8}(0.002)$
On further calculating we get,
$\Delta \mathrm{y}=\frac{-0.5}{1000}=-0.0005$
On substitution we get,
$-0.005=\frac{1}{(2.002)^{2}}-\frac{1}{4}$
We get
$\frac{1}{(2.002)^{2}}=0.2495$

Differentials, errors and approximations exercise 13.1 question 9 (viii)

Answer: 1.396368
Hint: Here, we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\log _{10} 4=0.6021$
$\log _{10} \mathrm{e}=0.4343$
Solution:
consider $\mathrm{y}=\log _{10} x$
Or $\mathrm{y}=\frac{\log _{10} \mathrm{x}}{\log _{10} \mathrm{e}}$
We get
$y=0.4343 \log _{e} x$
Here
$\mathrm{x}=4 \text { and } \Delta \mathrm{x}=.04$
On differentiating wrt $x$
$\begin{aligned} &\frac{d y}{d x}=\frac{0.4343}{x} \Delta \mathrm{x} \\\\ &\text { At } \mathrm{x}=4 \\\\ &\frac{d y}{d x}=\frac{1}{4} \end{aligned}$
$\begin{aligned} &\text { So }, \Delta y=\frac{d y}{d x} d x=\frac{1}{4} 0.04=0.01 \\\\ &\text { i.e } \Delta y=0.01 \\\\ &\text { Therefore } \log _{\mathrm{e}} 4.04=\mathrm{y}+\Delta \mathrm{y}=1.396368 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (ix)

Answer: $2.3046$
Hint: Here we use
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\log e 10.2=2.3026$
Solution:
Consider $y=\operatorname{loge} x$
Here $x=10 \text { and } \Delta x=0.02$
By Differentiating w.r.t x,
So we get
$\Delta y=\frac{d y}{d x} \Delta x$
$\Rightarrow \Delta y=\frac{d y}{d x} \Delta x=\frac{1}{10} \times 0.02$
on further calculation
$\begin{aligned} &\Delta y=\frac{0.02}{10}=0.002 \\\\ &\Rightarrow \Delta y=f(x+\Delta x)-f(x) \\\\ &0.002=\operatorname{loge}(10+0.02)-\operatorname{loge} 10 \end{aligned}$
It can be written as
$0.002=\operatorname{loge} 10.02=2.3026$
We get,
$\log 10.02=2.3026$

Differentials, errors and approximations exercise 13.1 question 9 (x)

Answer: $1.004343$
Hint: Here we use
$\Delta y=f(x+\Delta x)-f(x)$
Given:
Solution:
let $x=10$
$x+\Delta x=10.1$
Then
$\begin{aligned} &\Delta x=0.1 \\\\ &\text { For } x=y \log _{10}=1 \\\\ &\text { Let: } d x=\Delta x=0.1 \end{aligned}$ $\begin{aligned} &\Delta x=0.1 \\\\ &\text { For } x=y \log _{10}=1 \\\\ &\text { Let: } d x=\Delta x=0.1 \end{aligned}$ $\begin{aligned} &\Delta x=0.1 \\\\ &\text { For } x=y \log _{10}=1 \\ &\text { Let: } d x=\Delta x=0.1 \end{aligned}$
Now, $y=\log _{10} x=\frac{\log e x}{\log e 10}=\frac{1}{2.3025 x}$
$\begin{aligned} &\left(\frac{d y}{d x}\right)_{x=10}=0.04343 \\\\ &\Delta y=d y=\frac{d y}{d x} x d x=0.04343 \times 0.1 \\\\ &\Delta y=0.004343 \end{aligned}$

$\log _{10} 10.1=y+\Delta y=1.004343$

Differentials, errors and approximations exercise 13.1 question 9 (xi)

Answer: $0.4849$

Hint: $f(x+\Delta x)=f(x)+\Delta f(x)$
Given: $f(x)=\cos x=\cos 60^{\circ}$
$\Delta x=1=0.01745 \text { radius }$
Solution:
$\cos 61^{\circ}=f\left(61^{\circ}\right)=f\left(60^{\circ}+1^{\circ}\right)=f\left(60^{\circ}\right)+\Delta x f^{1}\left(60^{\circ}\right)=0.5+[0.01745]$
$\left[-\sin 60^{\circ}\right]$
$\begin{aligned} &{\left[\therefore f^{1}(x)=-\sin x\right]} \\\\ &\Rightarrow \cos 61^{\circ}-0.5+(0.01745)(-0.86603) \\\\ &\therefore \cos 61^{\circ}=0.4848 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xiv)

Answer: $0.57560442$
Hint: Here, we use $f(x+\Delta y)-f(x)$
Given: $\cos \left(\frac{11 \pi}{36}\right)$
Solution: Let $x=\frac{12 \pi}{36}=\frac{\pi}{3}$
$\begin{aligned} &\text { So, } x+\Delta x=\frac{\pi}{36} \\\\ &\Rightarrow \Delta x=\frac{-\pi}{36}=\frac{-22}{7}=-0.0873 \end{aligned}$

Differentiating $f(x)$
$\frac{d f}{d x}=\frac{d}{d x}(\cos x)$
we know
$\begin{aligned} &\frac{d}{d x}(\cos x)=-\sin x \\\\ &\frac{d f}{d x}=-\sin x \end{aligned}$
when, $x=\frac{\pi}{3}$
we have
$\frac{d f}{d x}=-\sin \left(\frac{\pi}{3}\right)$
$\begin{aligned} &\Rightarrow\left(\frac{d f}{d x}\right)_{x=\frac{\pi}{3}}=-0.86603 \\\\ &\Rightarrow f(x+\Delta x)-f(x) \\\\ &\Delta y=\left(\frac{d y}{d x}\right) \Delta x \end{aligned}$
$\begin{aligned} &\text { Here, } \frac{d f}{d x}=-0.86603 \\\\ &\Delta x=0.0873 \\\\ &\Rightarrow \Delta f=0.07560442 \end{aligned}$
now, we have
$\begin{aligned} &f\left(\frac{11 \pi}{36}\right)=f\left(\frac{\pi}{3}\right)+\Delta f \\\\ &f\left(\frac{11 \pi}{36}\right)=\cos \left(\frac{\pi}{3}\right)+0.07560442 \end{aligned}$
$\begin{aligned} &f\left(\frac{11 \pi}{36}\right)=0.5+0.07560442 \\\\ &f\left(\frac{11 \pi}{36}\right)=0.57560442 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xvi)

Answer: $3.074$
Hint: Here, we use
$\Delta y=f(x)+\Delta x)-f(x)$
Given: $29^{\frac{1}{2}}$
Solution: $y=f(x)=(x)^{\frac{1}{3}}$
$\begin{aligned} &\Rightarrow \text { let } \\\\ &x=27 \\\\ &x+\Delta x=29 \end{aligned}$
Thus,
$\begin{aligned} &\Delta x=2 \\\\ &\text { For } x=27 \\\\ &y=(27)^{\frac{1}{3}}=3 \end{aligned}$
Let $d x=\Delta x=2$
Now, $y=(x)^{\frac{1}{3}}$
$\Rightarrow \frac{d y}{d x}=\frac{1}{3 x^{\frac{1}{3}}}$
$\begin{aligned} &\left(\frac{d y}{d x}\right)_{x=27}=\frac{1}{27} \\\\ &\Delta y=d y=\frac{d y}{d x} d x=\frac{1}{27} \times 2=0.074 \end{aligned}$
$\begin{aligned} &\Delta y=0.074 \\\\ &\text { Hence, } 29^{\frac{1}{3}}=3+0.074=3.074 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xvii)

Answer: $4.042$
Hint: here we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $66^{\frac{1}{3}}$
Solution: Consider the function $y=f(x)=x^{\frac{1}{3}}$
Let,
$\begin{aligned} &x=64 \\\\ &x+\Delta x=66 \end{aligned}$
Then,
$\begin{aligned} &\Delta x=2 \\\\ &\Rightarrow \text { for } x=64 \\\\ &y=(64)^{\frac{1}{3}}=4 \end{aligned}$
Let,
$\begin{aligned} &d x=\Delta x=2 \\\\ &\text { Now, } y=\left(x^{\frac{1}{3}}\right) \\\\ &\frac{d y}{d x}=\frac{1}{3(x)^{\frac{2}{3}}} \\\\ &\left(\frac{d y}{d x}\right)=\frac{1}{48} \end{aligned}$
$\begin{aligned} &\Delta y=d y=\frac{d y}{d x} d x=\frac{1}{48} \times 2=0.042 \\\\ &\Delta y=0.042 \\\\ &(66)^{\frac{1}{3}}=y+\Delta y=4.042 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9(xviii)

Answer: 5.1
Hint:Here, we use the formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\sqrt{26}$
Solution: Consider the function $y=f(x)=\sqrt{x}$
Let
$\begin{aligned} &x=25 \\\\ &x+\Delta x=26 \end{aligned}$
Then,
$\begin{aligned} &\Delta x=2 \\\\ &\text { For } x=25 \\\\ &y=\sqrt{25}=5 \end{aligned}$
Let,
$d x=\Delta x=1$
Now
$y=(x)^{\frac{1}{2}}$
$\begin{aligned} &\frac{d y}{d x}=\frac{1}{2 \sqrt{x}} \\\\ &\left(\frac{d y}{d x}\right)_{x=25}=\frac{1}{10} \\\\ &\Delta y=d y=\frac{d y}{d x} \times d x=\frac{1}{10} \times 1=0.1 \end{aligned}$
$\begin{aligned} &\Delta y=0.1 \\\\ &\sqrt{26}=y+\Delta y=5.1 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xix)

Answer: 6.08
Hint: $\Delta y=f(x+\Delta x)-f(x)$
Let's use this formula
Given: $\sqrt{37}$
Solution: $\frac{d y}{d x}=\frac{1}{2 \sqrt{x}}$
So, we get
$\Delta y=\frac{d y}{d x} \Delta x$
So , we get
$\Delta y=\frac{1}{2 \sqrt{x}} \times 1$
on further calculation
$\Delta y=\frac{1}{12}=0.08$
we know that
$\Delta y=f(x+\Delta x)-f(x)$
By substituting the values,
$\begin{aligned} &0.08=\sqrt{36+1}-\sqrt{36} \\\\ &0.08=\sqrt{37}-6 \\\\ &\sqrt{37}=6.08 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xx)

Answer: 0.693
Hint: $\Delta y=f(x+\Delta x)-f(x)$
we use this formula
Given: $\sqrt{0.48}$
Solution: consider the function $y=f(x)=\sqrt{x}$
Let
$\begin{aligned} &x=0.49 \\\\ &x+\Delta x=0.48 \end{aligned}$
Then,
$\begin{aligned} &\Delta x=-0.01 \\\\ &\Rightarrow \text { for } x=0.49 \\\\ &y=\sqrt{0.19}=0.7 \end{aligned}$
Let,
$\begin{aligned} &d x=\Delta x=0.01 \\\\ &\Rightarrow \text { now } y=(x)^{\frac{1}{2}} \\\\ &\frac{d y}{d x}=\frac{1}{2 \sqrt{2 x}} \\\\ &\left(\frac{d y}{d x}\right)_{x=0.49}=\frac{1}{1.4} \end{aligned}$
$\begin{aligned} &\Delta y=d y=\frac{d y}{d x} \times d x=\frac{1}{1.4} \times(-0.01) \\\\ &\Delta y=-0.007143 \\\\ &\sqrt{0.48}=y+\Delta y=0.693 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xxi)

Answer: $3.00926$

Hint: Here we use below formula,
$\Delta y=f(x+\Delta x)-f(x)$
Given: $(82)^{\frac{1}{4}}$
Solution: $x=81$
$\Delta x=1$
on differentiating $f(x)$ with respect to $x$
$\frac{d f}{d x}=\frac{d}{d x}\left(x \frac{1}{4}\right)$
we know $\frac{d}{d x}\left(x^{3}\right)=n x^{n-1}$
$\begin{aligned} &\frac{d f}{d x}=\frac{1}{4} x^{\frac{1}{4}-1} \\\\ &\frac{d f}{d x}=\frac{1}{4} x^{\frac{3}{4}}=\frac{1}{4 x^{\frac{3}{4}}} \end{aligned}$
$\begin{aligned} &\Rightarrow \text { when } x=81 \text { we have } \frac{d f}{d x}=\frac{1}{4(81)^{\frac{3}{4}}} \\\\ &\Rightarrow \frac{d f}{d x}=\frac{1}{4(34)^{\frac{3}{4}}}=\frac{1}{4\left(3^{3}\right)}=\frac{1}{4 \times 27}=\frac{1}{108}=0.00926 \end{aligned}$
$\begin{aligned} &\Rightarrow \Delta y=\left(\frac{d y}{d x}\right) \Delta x \\\\ &\Delta f=0.00926 \\\\ &\Rightarrow \text { now, } f(82)=f(81)+\Delta f \end{aligned}$
$\begin{aligned} &f(82)=3+0.00926 \\\\ &f(82)=3.00926 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xxii)

Answer: 0.677

Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\left(\frac{17}{81}\right)^{\frac{1}{4}}$
Solution: Let $y=x \frac{1}{4}$
where $x=16 \text { and } \Delta x=1$
Since $y=x^ \frac{1}{4}$
$\frac{d y}{d x}=\frac{d\left(x ^\frac{1}{4}\right)}{d x}=\frac{1}{4} x^{\frac{1}{4}-1}=\frac{1}{4} x^{\frac{-3}{4}}=\frac{1}{4 x^{\frac{3}{4}}}$
$\begin{aligned} &\Rightarrow \text { Now, } \Delta y=\frac{d y}{d x} \Delta x=\frac{1}{4} \times \frac{1}{16^{\frac{3}{4}}} \times 1 \\\\ &=\frac{1}{4} \times \frac{1}{24^{\frac{3}{4}}}=\frac{1}{4} \times \frac{1}{2^{3}}=\frac{1}{32} \end{aligned}$
Now,
$(17)^{\frac{1}{4}}=y+\Delta y$
Putting values,
$\begin{aligned} &(17)^{\frac{1}{4}}=(16)^{\frac{1}{4}}+\Delta y \\\\ &(17)^{\frac{1}{4}}=(24)^{\frac{1}{4}}+\Delta y \end{aligned}$
$\begin{aligned} &(17)^{\frac{1}{4}}=2+\frac{1}{32} \\ &(17)^{\frac{1}{4}}=2.03125 \end{aligned}$
Now,
$\left(\frac{17}{81}\right)^{\frac{1}{4}}=\frac{2.03125}{3}=0.677$

Differentials, errors and approximations exercise 13.1 question 9 (xxiii)

Answer: 2.0125
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $(33)^{\frac{1}{5}}$
Solution: $(33)^{\frac{1}{5}}=(32+1)^{\frac{1}{5}}$
let $y=f(x)=x^{\frac{1}{5}}$
$\begin{aligned} &\Rightarrow y+\Delta y=(x+\Delta x)^{\frac{1}{5}} \\\\ &\Rightarrow \Delta y=(x+\Delta x)^{\frac{1}{5}}-x^{\frac{1}{5}} \end{aligned}$
Also,
$\begin{aligned} &\Delta y=f^{1}(x) \Delta x \\\\ &(x+\Delta x)^{\frac{1}{5}}-x^{\frac{1}{5}}=\frac{1}{5} x^{\frac{-4}{5}} \times \Delta x \end{aligned}$
Put $x=32, \Delta x=1$
$\begin{aligned} &(33)^{\frac{1}{5}}-(32)^{\frac{1}{5}}=\frac{1}{5}(2)^{4}(1) \\\\ &\Rightarrow(33)^{\frac{1}{5}}=2+0.0125=2.0125 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xxiv)

Answer: 6.05
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\sqrt{36.6}$
Solution: $y=\sqrt{x} \text { let } x=36 \text { and } A x=0.6$ then,
$\begin{aligned} &\Delta y=\sqrt{x+\Delta x}-\sqrt{x} \\\\ &=\sqrt{36.6}-\sqrt{36} \\\\ &=\sqrt{36.6}-6 \\\\ &\Delta y=\sqrt{36.6}-6 \end{aligned}$
now, $dy$ is approximate equal to $Ay$ and is given by.
$\begin{aligned} &d y=\left(\frac{d y}{d x}\right) d x=\frac{1}{2 \sqrt{x}}(0.6) \\\\ &\frac{1}{2 \sqrt{36}} \times 0.6=0.05 \end{aligned}$
The approximate value of $\sqrt{36.6} \text { is } 6+0.05=6.05$

Differentials, errors and approximations exercise 13.1 question 9 (xxv)

Answer: $25^{\frac{1}{3}}=2.926$
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $25^{\frac{1}{3}}$
Solution: Let $y=x^{\frac{1}{3}}$
where $x=27 \text { and } \Delta x=-2$
Since $y=x^{\frac{1}{3}}$
$\begin{aligned} &\frac{d y}{d x}=\frac{d\left(x \frac{1}{3}\right)}{d x} \\\\ &=\frac{1}{3} x^{\frac{1}{3}-1} \\\\ &=\frac{1}{3} x^{\frac{-2}{3}}=\frac{1}{3 x^{\frac{2}{3}}} \end{aligned}$
Now,
$\Delta y=\frac{d y}{d x} \Delta x$
Putting values
$\begin{aligned} &\Delta y=\frac{1}{3(27)^{\frac{2}{3}}} \times(-2) \\\\ &\Delta y=\frac{-2}{3 \times\left(3^{3}\right)^{\frac{2}{3}}}=\frac{2}{3 \times 3^{2}}=\frac{2}{27}=-0.074 \end{aligned}$
$\begin{aligned} &(25)^{\frac{1}{3}}=3-0.074 \\\\ &(25)^{\frac{1}{3}}=2.926 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xxvi)

Answer: 7.036
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\sqrt{49.5}$
Solution: $\text { let } f(x)=\sqrt{x} \quad \text { where } x=49$
$\text { Let } \Delta x=0.5$
$f(x+\Delta x)=\sqrt{x+\Delta x}=\sqrt{49.5}$
Now by definition approximately we can write
$\begin{aligned} &f{}'(x)=\frac{f(x+\Delta x)-f(x)}{\Delta x} \\\\ &f(x)=\sqrt{x}=\sqrt{49}=7 \\\\ &\Delta x=0.5 \\\\ &\Rightarrow f(x)=\frac{1}{2 \sqrt{x}}=\frac{1}{2 \sqrt{49}}=\frac{1}{14} \end{aligned}$
putting values in (i) we get,
$\begin{aligned} &\frac{1}{14}=\frac{\sqrt{495}-7}{0.5} \\\\ &\sqrt{49.5}=\frac{0.5}{14}+7=\frac{05+98}{14}=\frac{485}{14} \\\\ &=7.036 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xxvii)

Answer: 7.904
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $(3.968)^{\frac{3}{2}}$
Solution: $\text { let } y=f(x)=x^{\frac{3}{2}}, x=4$
$\begin{aligned} &x+\Delta x=3.968 \\\\ &\Delta x=-0.032 \\\\ &\Delta y=\left[\frac{d y}{d x}\right]_{x=4} \times \Delta x \end{aligned}$
$\begin{aligned} &\Delta y=\left[\frac{3}{2} x^{\frac{1}{2}}\right]_{x=4} \times \Delta x \\\\ &\Delta y=\frac{3}{2} \times 2(-0.032)(0.096) \\\\ &(3.968)^{\frac{3}{2}}=f(x+\Delta x) \end{aligned}$
$\begin{aligned} &=f(x)+\Delta y \\\\ &=8-0.096 \\\\ &=7.904 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xxviii)

Answer: 31.920
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $(1.999)^{5}$
Solution: $\operatorname{let} x=2 \text { and } \Delta x=-0.001$
$\text { Let } y=x^{5}$
on differentiating both side wrt we get
$\begin{aligned} &\frac{d y}{d x}=5 x^{4} \\\\ &\text { Now, } \Delta y=\frac{d y}{d x} \Delta x=5 x^{4} \times \Delta x \\\\ &=5 \times 2^{4} \times[-0.001]=-80 \times 0.001 \end{aligned}$
$\begin{aligned} &=-0.080 \\\\ &(1.999)^{5}=y+\Delta y=2^{5}+(-0.080) \\\\ &=32-0.080 \\\\ &=31.420 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 9 (xxix)

Answer: 0.2867
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\sqrt{0.082}$
Solution: $\text { let } f(x)=\sqrt{x}$
Using $f(x+\Delta x)=f(x)+\Delta x \times f(x)$
Taking $x=09 \text { and } \Delta x=-0.008$
We get $f(0.09-0.008)=f(0.09)+(-0.008)(0.09)$
$\begin{aligned} &\Rightarrow \sqrt{0.082}=\sqrt{0.09}-0.0008 \times \frac{1}{2 \sqrt{0.09}} \\\\ &=0.3-\frac{0.008}{0.6} \\\\ &=0.3-0.01333=0.2867 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 10

Answer: 28.21
Hint: Here we use this below formula
$f(x+\Delta x)-f(x)=\Delta y$
Given: $f(2.01), f(x)=4 x^{2}+5 x+2$
Solution: $f 2.01=f(x+\Delta x)$
$=4(x+\Delta x)^{2}+5(x+\Delta x)+2$
$\begin{aligned} &\Delta y=f(x+\Delta x)-f(x) \\\\ &\Rightarrow f(x)+f(x) x \Delta x \\\\ &f(2.01)=\left(4 x^{2}+5 x+2\right)+(8 x+5) \Delta x \end{aligned}$
$\begin{aligned} &=\left(4(2)^{2}+5((2)+2)[8(2)+5](0.01)\right. \\\\ &=(16+10+2)+(16+5)(0.01) \\\\ &=28+0.21 \\\\ &=28.21 \end{aligned}$
Hence, the approximate value of $f(2.01) \text { is } 28.21$

Differentials, errors and approximations exercise 13.1 question 11

Answer: 34.495
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $x^{3}-7 x^{2}+15$
Solution: $x=5 \Delta x=0.001$
⇒ then we have,
$\begin{aligned} &f(5.001)=f(x+\Delta x)=(x+\Delta x)^{2}-7(x+\Delta x)^{2} \\ &=f 15 \end{aligned}$
Now, $\Delta y=f(x+\Delta x)-f(x)$
$\begin{aligned} &\therefore f(x+\Delta x)=f(x)+\Delta y \\\\ &=f(x)+f(x) \Delta x \\\\ &\Rightarrow f(5.001)=\left(x^{3}-7 x^{2}+15\right)+\left(3 x^{2}-14 x\right) \Delta x \\\\ &=\left[(5)^{3}-7(5)^{2}+15\right]+\left[3(5)^{2}-14(5)\right](0.001) \end{aligned}$
$\begin{aligned} &=-35+(s)(0.001) \\\\ &=-35+0.005 \\\\ &=-34.995 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 12

Answer: 3.0021715
Hint: Here we use this below formula
$\Delta y=f(x+\Delta x)-f(x)$
Given: $\log _{10} e=0.4343$
Solution: Let: $y=f(x)=\log _{10} x$
⇒ Here,
$\begin{aligned} &x=1000 \\\\ &x+\Delta x=1005 \\\\ &\Delta x=5 \\\\ &d x=\Delta x=5 \end{aligned}$
$\begin{aligned} &\text { For } x=1000 \\\\ &y=\log _{10} 1000=\log _{10}(10)^{3}=3 \\\\ &\Rightarrow \text { Now } y=\log _{10} x=\frac{\log e x}{\log e 10} \\\\ &\frac{d y}{d x}=\frac{0.4343}{x} \end{aligned}$
$\begin{aligned} &\left(\frac{d y}{d x}\right)_{x=1000}=\frac{0.4343}{1000}=0.00043 \\\\ &\Delta y=d y=\frac{d y}{d x} \times d x=0.0004343 \times 5=3.0021715 \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 13

Answer: $2.16 \pi m^{2}$
Hint: Here, we use the surface area of the sphere (s)
$s=4 \pi r^{2}$
Given: $r=9 \mathrm{~m} \text { and } \Delta r=0.03 \mathrm{~m}$
Solution: $s=4 \pi r^{2}$
$\begin{aligned} &\frac{d s}{d x}=8 \pi r \\\\ &d s=\left(\frac{d s}{d x}\right) \Delta r \\\\ &=(8 \pi r) \Delta r \end{aligned}$
$\begin{aligned} &=8 \pi(9)(0.03) m^{2} \\\\ &=2.16 \pi m^{2} \end{aligned}$

⇒ Hence, the approximate error in circulating the surface area is $2.16 \pi m^{2}$

Differentials, errors and approximations exercise 13.1 question 14

Answer: 2% decrease
Hint: Here, we use the formula of surface area of cube
$s=6 x^{2}$
Given: $\Delta x=1 \% \text { decrease }$
Solution:
$\begin{aligned} &\Delta x=(-0.01) x \\\\ &d s=\frac{d s}{d x} \times \Delta x=6 \times 2 \Delta x \end{aligned}$
$\begin{aligned} &=6 \times 2 x \times(-0.01 x) \\\\ &=-0.12 x^{2} \end{aligned}$
Therefore $-0.12x^{2}$ is the approximate change in surface area of cube

Differentials, errors and approximations exercise 13.1 question 15

Answer: $3.92 \pi \mathrm{m}^{3}$
Hint: Here volume $V$ the so here is given by $V=\frac{4}{3} \pi r^{3}$
Given: $r=7 \mathrm{~m} \text { and } \Delta r=0.02 \mathrm{~m}$
Solution: $\frac{d v}{d x}=4 \pi r^{2}$
$\begin{aligned} &\Delta v=d v\left(\frac{d v}{d r}\right) \Delta r=4 \pi r^{2} \Delta r \\\\ &=4 \pi(7)^{2}(0.02)=3.92 \pi m^{3} \end{aligned}$

Differentials, errors and approximations exercise 13.1 question 16

Answer: $0.03 x^{3} m^{3}$
Hint: Here we use the formula of a cube of side $x$ is given by $v=x^{3}$
Given: 1% increasing
Solution: $\left(\frac{d v}{d r}\right) \Delta x$
$\begin{aligned} &=3 x^{2} \Delta x \\\\ &=3 x^{2} \times 0.01 x \\\\ &=0.03 x^{3} \end{aligned}$
⇒ hence the approximate change in the volume of the cube is $0.03 x^{3} m^{3}$

RD Sharma class 12th exercise 13.1 is a top choice for students who are going to sit for their board exams pretty soon. Ex-students and toppers also recommend using this NCERT solution because they have benefitted from it in their board exams. The class 12 RD Sharma chapter 13 exercise 13.1 solution book so that aspiring students can experience the magic of using RD solutions for themselves.

Here is a list of reasons why the class 12 RD Sharma chapter 13 exercise 13.1 solution book is such a popular choice for students:-

The RD Sharma class 12th exercise 13.1 board exam preparations as many students have found common questions from the book in their maths papers. Common Questions can be solved quickly and will fetch a high score in exams.
RD Sharma class 12 solutions chapter 13 ex 13.1 can be great for self-study, especially when there are exams upcoming. It's impossible to read everything the day before exams, so students can use these solutions to test their knowledge.
Maths requires plenty of self-practice for perfection. In this case, the answers in the RD Sharma class 12 solutions chapter 13 ex 13.1 can be used by students to check their own answers and mark their progress.
School homework can also be solved by using RD Sharma class 12 solutions chapter 13 ex 13.1 at home. Teachers like to test students by giving questions from this book and exercise to check if they are up to date with their lessons. Hence, students can seek help from the book when they are stuck with difficult questions.
Experts have created the RD Sharma class 12 solutions Differentials, Errors and Approximations ex 13.1 book and they belong to the education sector. Therefore, students will find some new and interesting methods to help them with math questions.
The class 12 RD Sharma chapter 13 exercise 13.1 solution receives regular updates so that they correspond to questions in the NCERT textbooks. You can download the free pdf online from Career360.

RD Sharma Chapter wise Solutions

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

Frequently Asked Questions (FAQs)

1. How can I use RD Sharma class 12th exercise 13.1 to solve homework?

The RD Sharma class 12th exercise 13.1 solutions book is often used by teachers to give and check homework. Students can, therefore, seek the help of this book when they cannot answer difficult questions.

2. Is class 12 RD Sharma chapter 13 exercise 13.1 solution q good book?

The class 12 RD Sharma chapter 13 exercise 13.1 solution book is trusted by students and teachers in India. Experts have created the answers in the book so they are accurate and easy to understand.

3. Can I use RD Sharma class 12 solutions Differentials, Errors and Approximations ex 13.1 for JEE preparations?

Yes, students can definitely use RD Sharma class 12 solutions Differentials, Errors and Approximations ex 13.1 for their JEE mains preparations as they follow a similar syllabus.

4. How to download RD Sharma class 12 chapter 13 exercise 13.1 pdf?

The RD Sharma class 12 chapter 13 exercise 13.1 pdf can be easily downloaded from the Career360 website.

5. How many questions are there in RD Sharma class 12 chapter 13 exercise 13.1?

The RD Sharma class 12 chapter 13 exercise 13.1 book has a total of 10 questions based on the entire chapter.