Triangles And Parallelograms In Carpentry: A Fusion Of Mathematics And Craftsmanship In Class 9

Carpentry, the ancient craft of shaping wood into functional and aesthetic structures, relies heavily on mathematical concepts drawn directly from the Class 9 curriculum. The chapter on triangles and parallelograms, often overlooked by students as mere mathematical exercises, forms the very foundation of carpentry. This article discusses the mathematical principles and their applications, particularly for carpentry.

Geometry Behind The Artistry

The Class 9 maths curriculum introduces students to fundamental geometric concepts that inadvertently shape the world of carpentry. Before we explore their practical application, let's recap the core concepts discussed in the chapter.

Essence Of Area

At the heart of both mathematics and carpentry lies the concept of area. It quantifies the two-dimensional space enclosed by a geometric figure. In the realm of carpentry, precise area calculations are pivotal to optimising material utilisation and assessing resource requirements.

Congruence And Area Equivalence

A cornerstone of geometry is understanding that two congruent figures boast equal areas, although the converse is not necessarily true.

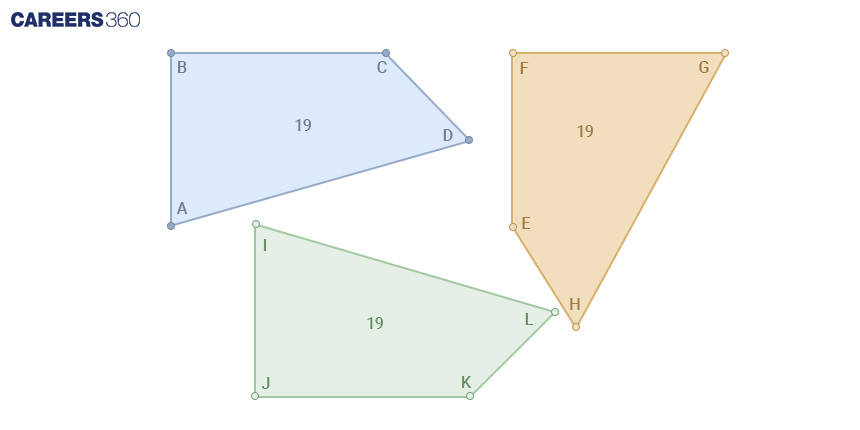
This principle resonates deeply with carpenters, who rely on this knowledge to ensure precise measurements and alignments in their creations.

Also check - Maternal Behaviour: How Do Animals Nurture Their Young Ones?

Merging Composite Figures

The chapter unveils methods to compute the area of a composite figure formed by combining distinct, non-overlapping regions. This concept echoes in the realm of carpentry, where intricate structures are often deconstructed into simpler components for calculation.

Parallelogram Area Formula

The formula for computing the area of a parallelogram:

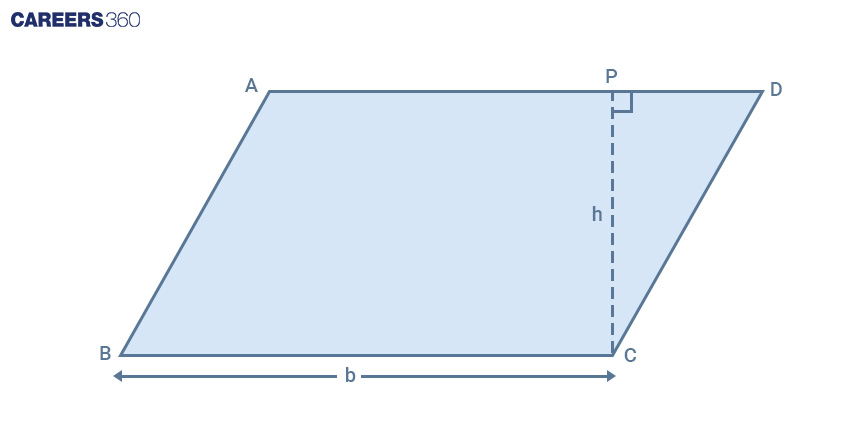
Consider a parallelogram ABCD with base BC as ‘b’ and height as ‘h’.

Area = Base * Altitude

Area = bh

This assumes substantial relevance in carpentry. Carpenters leverage this formula to ascertain the required surface area of materials like plywood or flooring.

Parallelograms And Common Bases

Carpenters frequently encounter parallelograms - quadrilaterals with opposite sides both parallel and of equal length. Understanding figures situated on the same base and between identical parallels is pivotal for maintaining accurate alignment in carpentry projects.

Consider two parallelograms, Parallelogram ABCD and Parallelogram ABEF, both sharing the same base and being located between the same pair of parallel lines.

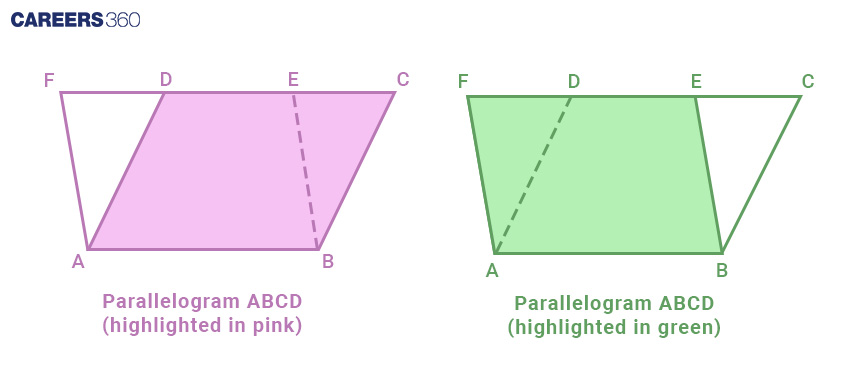
Let's denote the common base AB as "b" and the height (distance between the parallel lines) as "h." The height is perpendicular to the common base.

The formula to calculate the area of a parallelogram is

Area = base × height

For Parallelogram ABCD: Area₁ = b * h

For Parallelogram ABEF: Area₂ = b * h

Since both parallelograms have the same base and height, their areas are equal:

Area₁ = Area₂

b * h = b * h

This demonstrates that the area of parallelograms with common bases and between the same pair of parallel lines is indeed equal. The reason behind this equality is that both parallelograms share the same dimensions (base and height), and the area formula takes these dimensions into account, resulting in the same area for both shapes.

A Bridge Between Triangles And Parallelograms

The invaluable insight that the area of a triangle amounts to half that of a parallelogram with matching base and height unfurls a world of possibilities.

Let's consider a parallelogram ABCD and triangle ABE as shown below, with common base AB.

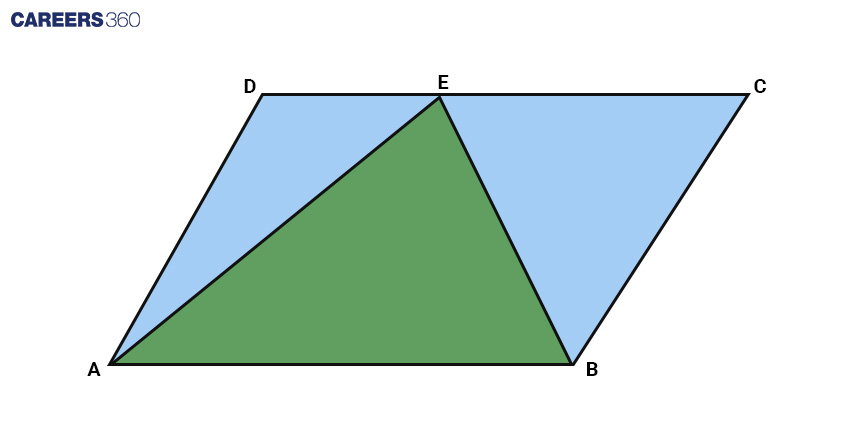
We know that

the Area of a triangle = (1/2) * base * height

And the Area of a parallelogram = base * height

This shows that the area of a triangle is half of the area of a parallelogram when both have the same base and same height. Carpenters employ this principle when constructing triangular roof structures or inclined supports.

Equal Areas And Parallel Lines

Understanding that figures boasting equal areas rest between identical parallels resonate deeply with carpenters. This comprehension underpins the quest for symmetry and equilibrium in woodworking projects.

Dividing Medians

In the carpentry realm, creating equal divisions within structures is a recurring necessity. The concept of medians bisecting triangles into two regions of equal area is a carpenter’s ally, ensuring precision in element arrangement.

Applying Mathematics To Craftsmanship

Now, let’s transition from theory to practice and explore practical scenarios where these mathematical tenets shape carpenters’ work.

Example 1: Flooring Precision

Imagine a carpenter embarking on installing wooden flooring in a room. Conceptualise each floorboard as a parallelogram, with its length as the base and the perpendicular distance from the floor to the bottom of the board as the altitude. Calculating the area to be covered now becomes a straightforward application of the parallelogram area formula.

Problem:

Suppose a carpenter is installing floorboards with a length of 1.5 metres and an altitude of 0.2 metres. Calculate the area covered by each floorboard.

Solution:

Area = Base * Altitude

Area = 1.5 metres * 0.2 metres

= 0.3 square metres

Example 2: Crafting Roof Trusses

Crafting roof trusses entails erecting triangular structures that offer support to the roof. The insight that a triangle's area equates to half that of a parallelogram with equivalent base and height assumes direct relevance here. Carpenters rely on this relationship to ascertain the requisite material for truss components.

Problem:

A carpenter is constructing a triangular roof truss with a base of 4 metres and a height of 3 metres. Determine the area of the triangular truss.

Solution:

Area = 0.5 * Base * Height

Area = 0.5 * 4 metres * 3 metres

= 6 square metres

Example 3: Precision Door Frame Alignment

During door frame installation, precision is paramount. Ensuring that the frame is aligned and vertical aligns with the concept of figures sharing the same base and lying between identical parallels. By validating that the sides of the door frame are parallel and accurately aligned, carpenters fashion sturdy and well-fitted frames.

Problem:

A carpenter is installing a door frame with sides that are 80 centimetres apart and a height of 2 metres. Are the sides of the door frame parallel?

Solution:

Yes, the sides of the door frame are parallel as they are equidistant and maintain the same distance of 80 centimetres throughout their length.

Example 4: Reinforcing Structures

Carpenters often need to create triangular supports or braces to bolster structures. The principle that triangles with equal base and height boast the same area contributes to stability. By distributing forces uniformly, these triangular supports enhance structural integrity.

Problem:

A carpenter needs to reinforce a shelf with triangular brackets. Each bracket has a base of 15 centimetres and a height of 20 centimetres. Calculate the area of each triangular bracket.

Solution:

Area = 0.5 * Base * Height

Area = 0.5 * 15 centimetres * 20 centimetres

= 150 square centimetres

Classroom And Beyond: Board Exam Relevance

The concepts discussed within this chapter resonate not only with carpenters but also with students preparing for board exams such as CBSE Class 10 or state boards as well. These assessments gauge students’ grasp of geometry and their capacity to wield mathematical principles in practical settings.

Also check - What Is The Physics Behind Rocket Boosters?

Expect to encounter questions that beckon students to:

• Compute areas of composite figures by dissecting them into simpler shapes.

• Demonstrate cognizance of congruence and area parity.

• Apply the formula for parallelogram area to address tangible problems.

• Expound upon the nexus between triangles and parallelograms boasting shared base and height.

• Resolve quandaries entailing medians and equal triangle areas.

Hope you have now gained a comprehensive understanding of Triangles And Parallelograms, and their applications, particularly in woodwork by carpenters.