Euler's Formula And Topology: A Discussion On Polyhedra

Polyhedra, those intriguing three-dimensional shapes with flat faces and sharp edges, have fascinated people for centuries. They can be found in famous buildings like the Great Pyramid of Giza, in incredible artwork like MC Escher's mind-bending drawings, and even in the tiny structures of crystals. These shapes are not just visually captivating; they hide a remarkable mathematical secret that has intrigued mathematicians for centuries.

In this article, we'll explore the world of polyhedra, discuss Euler's formula, and unveil the beauty of these geometric wonders.

What Are Polyhedra?

Polyhedra are three-dimensional shapes with flat surfaces, straight edges, and sharp corners. Think about a dice – it's a classic example of a polyhedron. A polyhedron can have many sides, and they can be triangles, squares, pentagons, or any other flat shape.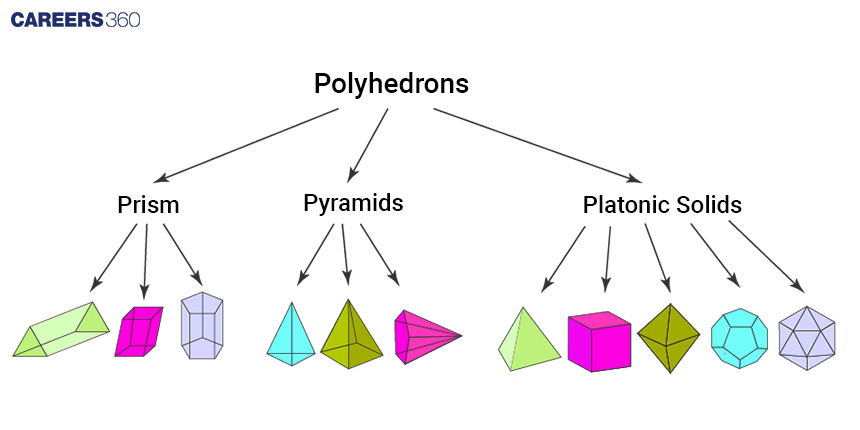

Polyhedra are all around us. When you look at a box, a soccer ball, or even a pyramid, you're looking at polyhedra. These shapes have fascinated people for centuries because they come in so many different forms and sizes.

Great Pyramid Of Giza

One of the most famous polyhedra in the world is the Great Pyramid of Giza. This ancient wonder of architecture is a massive polyhedron with a square base and four triangular sides. It was built thousands of years ago in Egypt and is still standing today.

The Great Pyramid is a testament to the skill and knowledge of the ancient Egyptians. They used polyhedra to create this incredible structure, and it's an enduring symbol of their civilization's greatness.

The Molecular World Of Polyhedra

Polyhedra aren't just found in the human-made world; they also exist in the natural world. One fascinating example is the molecular structure of crystals. Crystals are made up of repeating units, and these units often have a polyhedral shape.

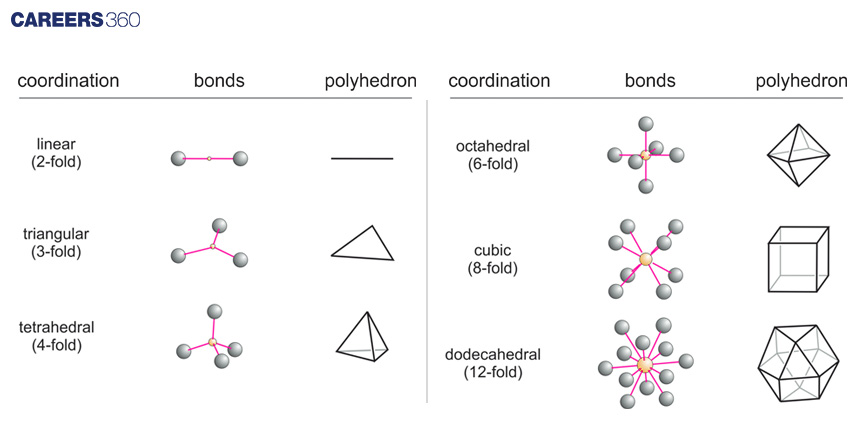
The arrangement of atoms or molecules in crystals follows specific patterns, and these patterns are often based on polyhedral shapes. This connection between polyhedra and the molecular world highlights the importance of these shapes in understanding the building blocks of matter.

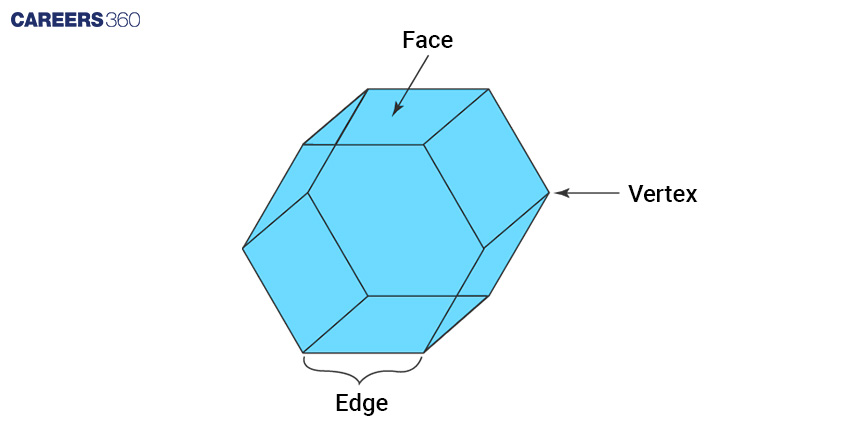
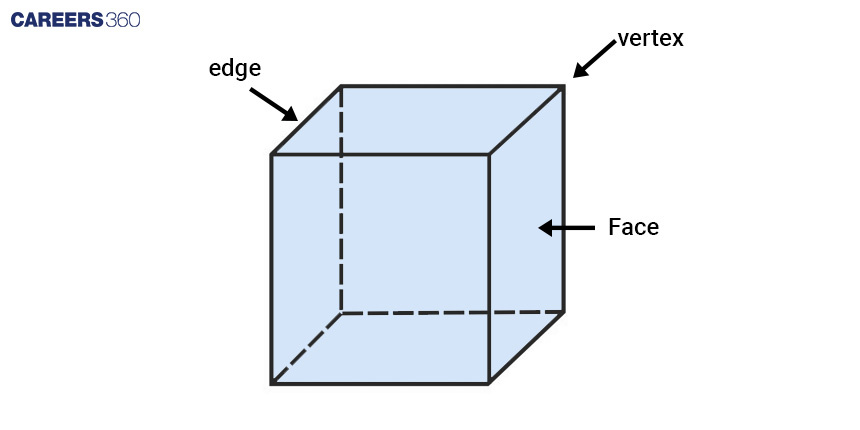
Components Of A Polyhedron

A polyhedron's characteristics are categorised into faces, edges, and vertices.

Face: The term 'face' refers to the flat surface of a polyhedron.

Edge: An 'edge' is a line where two faces meet.

Vertices: A 'vertex' is the point where two edges intersect.

Refer to the illustration depicting the face, vertex, and edges of a polyhedron for visual clarity.

Types Of Polyhedra

Polyhedra are primarily categorised into two groups:

(i) regular polyhedra and (ii) irregular polyhedra.

Regular Polyhedron

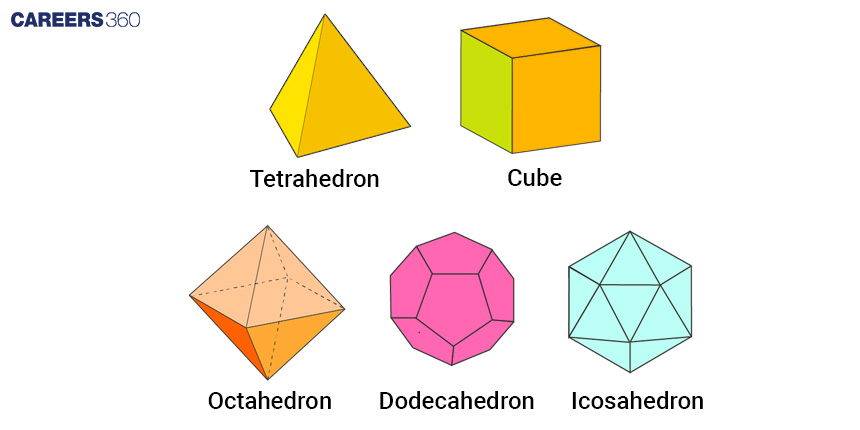
A regular polyhedron, also known as a Platonic solid, possesses faces that are regular polygons and are identical to each other. In a regular polyhedron, all the polyhedral angles are equal. There exist five regular polyhedra. The following is a listing of these five regular polyhedra:

>> Tetrahedron: A tetrahedron boasts 4 faces, 6 edges, and 4 vertices (corners); each face is in the shape of an equilateral triangle.

>> Cube: A cube comprises 6 faces, 12 edges, and 8 vertices; each face is a square.

>> Regular Octahedron: A regular octahedron encompasses 8 faces, 12 edges, and 6 vertices; each face is an equilateral triangle.

>> Regular Dodecahedron: A regular dodecahedron features 12 faces, 30 edges, and 20 vertices; each face is a regular pentagon.

>> Regular Icosahedron: A regular icosahedron possesses 20 faces, 30 edges, and 12 vertices; each face is an equilateral triangle.

Refer to the different types of regular polyhedra for visual reference.

Non-Regular Polyhedron

A polyhedron characterised by irregular polygonal faces that are dissimilar and do not share congruence, and in which the polyhedral angles are not uniform, is referred to as a non-regular polyhedron.

Euler's Formula

Now, let's discuss Euler's formula. This formula, created by the 18th-century Swiss mathematician Leonhard Euler, is a simple equation that has profound implications for polyhedra.

Euler's formula is all about the relationship between the number of vertices (corners), edges (straight lines connecting corners), and faces (flat surfaces) of a polyhedron. It's written as V - E + F = 2.

Here's what it means:

V = number of vertices (corners).

E = number of edges (straight lines).

F = number of faces (flat surfaces).

The formula says that if you add the number of vertices to the number of faces and then subtract the number of edges, you'll always get 2 for a convex polyhedron. Convex means that the polyhedron has no dents or holes in its surface.

Euler's formula might seem simple, but it's incredibly powerful. It's like a hidden code that reveals the secrets of polyhedra.

Also check - Blindness: How Much Can Visually Impaired People See?

Why Is Euler's Formula Important?

Euler's formula is crucial because it helps us understand and classify polyhedra. Let's break down its significance:

>> Classification: Euler's formula allows mathematicians to classify polyhedra into different categories. For example, there are regular polyhedra (also known as Platonic solids), like the cube or tetrahedron, which have specific properties that satisfy Euler's formula. This classification helps us understand the fundamental differences between different types of polyhedra.

>> Topology: Euler's formula is essential in the field of topology, which studies the properties of shapes that remain the same under continuous deformations like stretching and bending. It helps mathematicians compare and categorise different shapes based on their fundamental properties. This is crucial not just for mathematics but also for understanding how shapes and structures behave in the real world.

>> Geometry: Understanding Euler's formula deepens our knowledge of geometry. It reveals the intricate relationships between the vertices, edges, and faces of polyhedra, providing a foundation for further exploration in this field.

>> Problem Solving: Euler's formula can also be used as a problem-solving tool. If you know the number of vertices, edges, or faces of a polyhedron, you can use the formula to find the missing piece of information. It's like a puzzle solver for 3D shapes.

Exploring Euler's Formula

Let's explore Euler's formula with a practical example. Consider a cube, which is a regular polyhedron with six faces, eight vertices, and twelve edges.

V (vertices) = 8

E (edges) = 12

F (faces) = 6

Now, let's use Euler's formula:

V - E + F = 2

8 - 12 + 6 = 2

It works! Euler's formula holds true for the cube. No matter how you manipulate the cube or any other convex polyhedron, the sum V - E + F will always be 2.

But Euler's formula isn't limited to regular polyhedra. You can apply it to irregular polyhedra as well. The formula helps us understand the underlying structure and beauty of these shapes, even when they don't have perfect symmetry.

Beyond Polyhedra

Euler's formula isn't limited to polyhedra alone; it has applications in various areas of mathematics and science. Here are a few examples:

>> Graph Theory: Euler's formula is closely related to graph theory, which deals with networks of connected points (vertices) and lines (edges). It plays a crucial role in solving problems related to networks and circuits.

>> Geographical Maps: In cartography (the science of map-making), Euler's formula helps in understanding the relationships between regions, borders, and vertices on maps.

>> Architecture and Engineering: Architects and engineers use the principles of polyhedra and Euler's formula when designing structures like bridges and buildings to ensure stability and balance.

>> Molecular Chemistry: In chemistry, Euler's formula is used to understand the structures of complex molecules, especially those with a three-dimensional arrangement of atoms.

Also check - Quantum Numbers: What Are The Rules for Electron Arrangement?

Polyhedra, with their intricate shapes and hidden symmetries, serve as a canvas for mathematical exploration and artistic expression. They have inspired mathematicians, artists, architects, and scientists for centuries, and they continue to do so today.