Fun Maths Puzzles: Attempt These To Hone Your Number Skills

Do you love playing with numbers and having fun while learning? If you're a student looking to improve your maths skills or just someone who finds maths intriguing, you're in for a treat. In this article, we've put together a collection of entertaining maths puzzles designed to make learning numbers enjoyable.

Maths puzzles are not only fun but also essential for students. They provide a unique way to boost your maths skills while enhancing critical thinking, problem-solving abilities, and creative reasoning. These puzzles encourage you to explore different aspects of numbers and make learning an engaging and memorable experience. First, Let's start with the basics of the number system.

Also, check - Measurement Accuracy: How Calculate The Area Of Your Home?

Numbers And Related Concepts

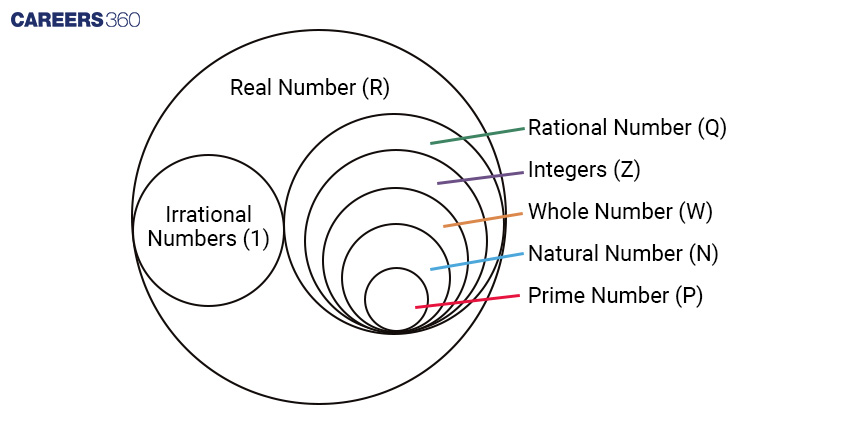
>> Natural Numbers are the numbers we use for counting things, like how many apples you have or how many friends you invite to a party. They start at 1 and keep going forever, with each number being one more than the one before it. It's like 1, 2, 3, 4, and so on. Natural numbers don't include negative numbers or zero

>> Whole numbers are like natural numbers, but they include one extra number: zero. They start with zero and then go on to the positive counting numbers, just like natural numbers. So, the whole numbers are 0, 1, 2, 3, 4, and so on.

>> Integers are like natural numbers, but they also include the numbers less than zero. So, they include all the positive numbers (like 1, 2, 3) and all the negative numbers (like -1, -2, -3), as well as zero. Integers are the whole numbers family, including both positive and negative members.

>> Rational numbers are a type of number that can be expressed as a fraction. A fraction is like having a part of something. For example, if you have 3/4 of a pizza, that's a rational number. Rational numbers include whole numbers and numbers with decimal parts that either stop or repeat.

>> Irrational numbers are a bit different from the numbers you use for everyday counting. They are numbers that cannot be expressed as simple fractions or ratios of two whole numbers. What makes them "irrational" is that their decimal expansions go on forever without repeating any pattern such as π and √2.

>> Real numbers are a group of numbers that includes everything you can think of when it comes to numbers. They cover all the numbers you encounter in your life, whether they are whole numbers, fractions, or decimals. Real numbers are like a big family of numbers that fills up the entire number line.

>> Prime numbers are special numbers that can only be divided by 1 and themselves. Prime numbers start with 2 and continue indefinitely. Less than 100, there exist 25 prime numbers, including 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.

>> Co-prime Numbers are pairs of numbers that have only 1 as their common factor. In other words, when you look at two co-prime numbers, you won't find any other number (except 1) that can divide both of them evenly. It's like a special kind of number friendship. For example, 15 and 28 are co-prime because the only number that can divide both of them evenly is 1. But 12 and 18 are not coprime because both can be divided by 6

>> Composite numbers are a bit different from natural numbers. While natural numbers are the ones we use for counting, composite numbers are natural numbers that are not prime. In other words, composite numbers have more than just two factors, unlike prime numbers that have only two factors (1 and the number itself). Some examples of composite numbers are 4, 6, 8, and 9.

The above type of numbers can be visualised as

>> Factors are numbers that you can multiply together to get your original number. For 12, its factors are 1, 2, 3, 4, 6, and 12 because you can multiply these numbers to make 12. Factors are like ingredients you mix to bake a cake. They're what you need to make the number.

>> Multiples are like the results of multiplying your number by different numbers. For 12, some of its multiples are 24, 36, 48, and so on. These are the "cakes" you get when you bake your "ingredient," which is 12. Multiples are what you get after multiplying.

>> Prime factorization is like taking a big number and breaking it down into its smallest building blocks, which are prime numbers. For instance, if you want to find the prime factorization of 12, you break it down into 2 x 2 x 3.

Prime factorization of a number N = p₁^a1p₂^a2p₃^a3...p_k^ak

Where p₁, p₂, p₃, ..., p_k are distinct prime numbers, and a₁, a₂, a₃, ..., a_k are their respective exponents.

Number of Factors = (a₁ + 1)(a₂ + 1)...(a_k + 1)

For example 12 = 2 * 2 * 3 = 2² * 3

Number of Factors = (2 + 1)(1 + 1) = 6

Fun Puzzles

Question 1: If we take a 3-digit number ABC and multiply it by a single-digit number D, we get a result that looks like 37DD, where A, B, C, and D are different digits, and none of them are zero. What is the sum of A, B, and C?

Solution:

We have three digit number: ABC

Here A, B, C, and D are single non-zero different digits

Therefore values can be 1, 2, 3, 4, 5, 6, 7, 8, and 9

Also the condition given is: ABCD = 37DD

This can also be rewritten as ABC = 37DD/D

Let's consider D = 1

ABC = 3711/1 = 3711 not as expected result

Consider D = 2

ABC = 3722/2 = 1861 not as expected result

Consider D = 3

ABC = 3733/3 not as expected result

Consider D = 4

ABC = 3744/4 = 936

We can observe that A, B, C, and D values are respectively 9, 3, 6, and 4 that are different digits. So A + B + C = 9 + 3 + 6 = 18

Consider D values = 5, 6, 7, 8, and 9

ABC = 3755/5 = 751 digit 5 is repeated so not as expected.

ABC = 3766/6 not divisible by 6

ABC = 3777/7 not divisible by 7

ABC = 3788/8 not divisible by 8

ABC = 3799/9 not divisible by 9

The only valid case is when D = 4 so that A, B, C, and D values are respectively 9, 3, 6, and 4 that are different digits.

Hence A + B + C = 9 + 3 + 6 = 18

Question 2: In the office of Yamraj, there are an equal number of chairs with four legs and tables with four legs, and the same number of stools with three legs as there are almirahs with four legs. If the number of stools is one more than the number of workers, and the total number of legs in the office is 585, how many workers are there?

Solution:

Given that the number of chairs with four legs = number of tables with four legs = Number Of Workers = X

Number of stools with three legs = number of almirahs with four legs = Y

Number of workers = Number of stools - 1 = Y - 1

Total number of legs = 585

Find: how many workers?

According to given conditions

4X + 4X + 3Y + 4Y + 2(Y - 1) = 585

X = Y - 1 ⇒ Y = X + 1

4X + 4X + 3(X + 1) + 4(X + 1) + 2(X) = 585

4X + 4X + 3X + 3 + 4X + 4 + 2X = 585

17X = 585 - 7

X = 578/17 = 34

Hence there are 34 workers

Question 3: How can a cricket player score 25 runs by hitting the ball for either 1 run, 4 runs, or 6 runs at a time, and in any order they like?

Solution: Consider different cases as given below in the table

We can observe that the total number of cases are 19 hence there are a total 19 different ways in which 25 runs can be scored.

Question 4: How many three-digit numbers (with no repeating digits) are there where each digit is an odd number, and the number can be divided by 5?

Solution: Given that the three-digit number with no repeating digits. Each digit is odd: 1, 3, 5, 7, 9. Number can be divided by five, therefore the unit digit can only be five.

Consider the following cases

Hence. total three digits numbers are 3*4 = 12

Question 5: ABC is a three-digit number. Where A, B, and C are non-zero integers. When the tenth place digit (B) is removed, the new number is AC. How many numbers are such that ABC = 9AC + 4C?

Solution: Given number ABC, and condition ABC = 9AC + 4C

Find: number of ways ABC can be written

ABC = 100A + 10B + C

9AC = 9(10A + C) = 90A + 9C

Thus

ABC = 100A + 10B + C = 90A + 9C + 4C

10A + 10B = 12C

5A + 5B = 6C

Consider C = 5

A + B = 6

Cases:

Hence, There are five numbers.

Also, check - How Do Parasites Survive By Exploiting Other Organisms?

Hope this gives you a better grasp of ideas like rational numbers, irrational numbers, prime numbers, co-prime numbers, factors, and how to work with number system challenges.