Smart Shopping CBSE Class 8: Comparing Quantities For Better Deals

In the fast-paced world of consumerism, smart shopping has become an essential skill. CBSE Class 8 introduces students to the concept of "Comparing Quantities," a mathematical skill that equips them to make informed decisions while shopping. This article will delve into the significance of comparing quantities in smart shopping, and how mastering this concept can help students excel not only in their exams like Maths Olympiads and Boards but also in competitive exams like JEE, CGL, CAT, and many more. Through solved examples, we will demonstrate how students can apply this knowledge in real-life scenarios to secure better deals.

Importance In Exams And Real-Life Applications

Scoring well in Maths olympiads and board exams

• Ratios and Percentages: Students must understand the relationship between two quantities in the form of ratios and express them as percentages.

• Profit and Loss: Solving questions on cost price, selling price, and profit percentage help in various problem-solving exercises.

• Discounts and Compound Interest: Students can excel in numerical problems involving discounts, compound interest, and instalment schemes.

Competitive Exams (JEE, CGL, CAT, etc.)

• Logical Reasoning: Comparing quantities trains students to identify patterns and make logical deductions, essential for competitive exams.

• Time Management: Efficiency in solving questions related to percentages and profit and loss helps manage time during exams.

• Data Interpretation: Mastery in comparing quantities aids in interpreting graphs and charts, frequently asked in competitive exams.

Also check - Improve Your Speed And Accuracy With The Fraction Percentage Table

Understanding Comparing Quantities

Comparing quantities involves evaluating different aspects of products or services to determine their value. In CBSE Class 8, this topic covers ratios, percentages, profit and loss, discounts, and compound interest. This mathematical foundation is invaluable in making optimal shopping choices.

Ratios And Proportions In Shopping

Comparing quantities involves the understanding of ratios and proportions, which are invaluable when evaluating different products or services. For instance, when choosing between two similar products with different quantities and prices, students can calculate their unit prices using ratios to determine which one offers better value for money.

Example: If a pack of 500g of cereal costs Rs. 200 and another pack of 750g costs Rs. 300, students can use ratios to find the cost of 1g of cereal for each pack. By comparing these unit prices, they can identify the better deal.

Students can memorise the below friction percentage table to do quick calculations and conversions from one quantity to another.

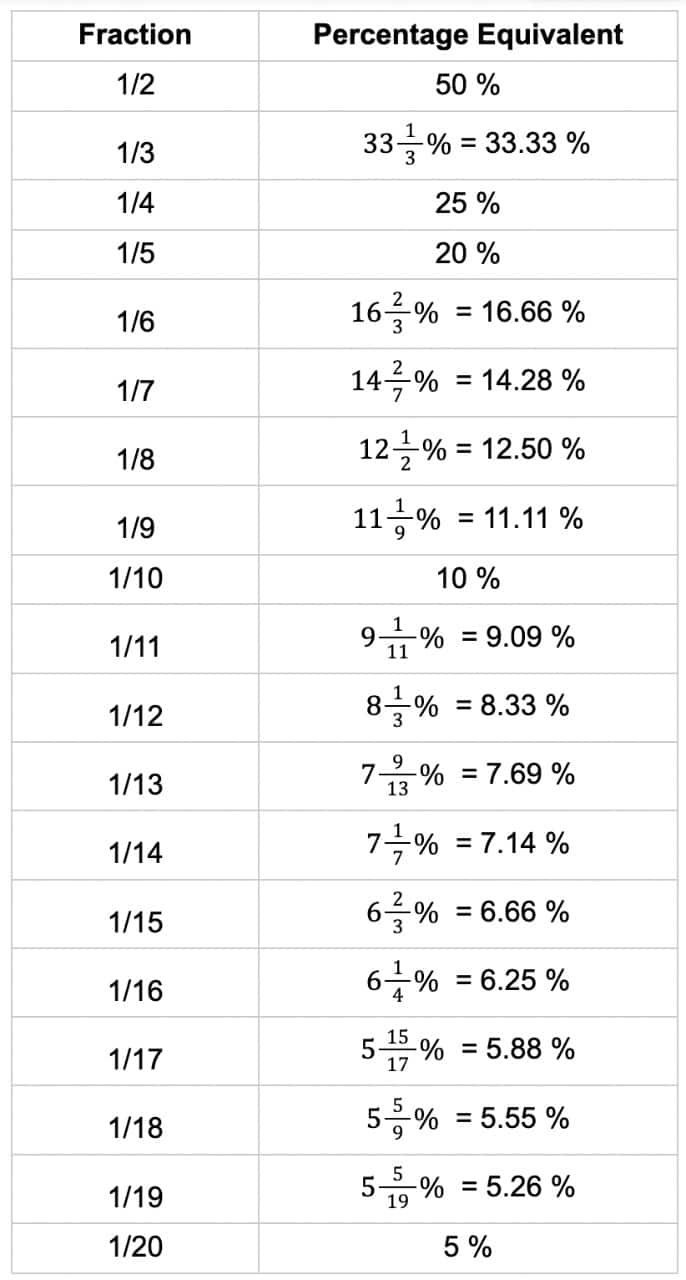
Problem 1: A customer bought a laptop for ₹80000, and the sales tax rate is 8%. Calculate the total amount the customer has to pay, including sales tax.

Solution:

Sales Tax Amount = 8% of ₹80000

= (8/100) * ₹80000

= ₹6400

Total Amount to Pay = Original Price + Sales Tax Amount

Total Amount to Pay = ₹80000 + ₹6400 = ₹86400

Therefore, the customer has to pay ₹86400, including sales tax.

Calculating Discounts And Savings

Knowing how to calculate discounts is an essential skill for smart shopping. Class 8 students learn to apply the concept of percentages to evaluate discounts offered by retailers. This knowledge empowers them to identify the actual price after the discount and make informed decisions while shopping.

Problem 1: Two stores are selling the same type of television. Store A offers the television for ₹1200 with a 10% discount, while Store B offers the television for ₹1100 with a 5% discount. Which store offers the better deal?

Solution:

Store A: Discount Amount = 10% of ₹1200

= 0.10 * ₹1200

= ₹120

Discounted Price = Original Price - Discount Amount

Discounted Price = ₹1200 - ₹120 = ₹1080

Store B:

Discount Amount = 5% of ₹1100

= 0.05 * ₹1100

= ₹55

Discounted Price = Original Price - Discount Amount

Discounted Price = ₹1100 - ₹55 = ₹1045

Comparing the discounted prices: Store A offers the television for ₹1080, and Store B offers it for ₹1045.

Therefore, Store B offers the better deal, as the television is cheaper at ₹1045 compared to ₹1080.

Profit And Loss Analysis

The ability to understand profit and loss is crucial for becoming a smart shopper. Class 8 students learn to apply percentage concepts to calculate profit margins and assess the actual cost of products or services after a discount or markup.

Let’s understand cost price, selling price, and profit percentage with an example of a Coke.

Also Check - Class 10: How Can I Get 100 Marks In Maths

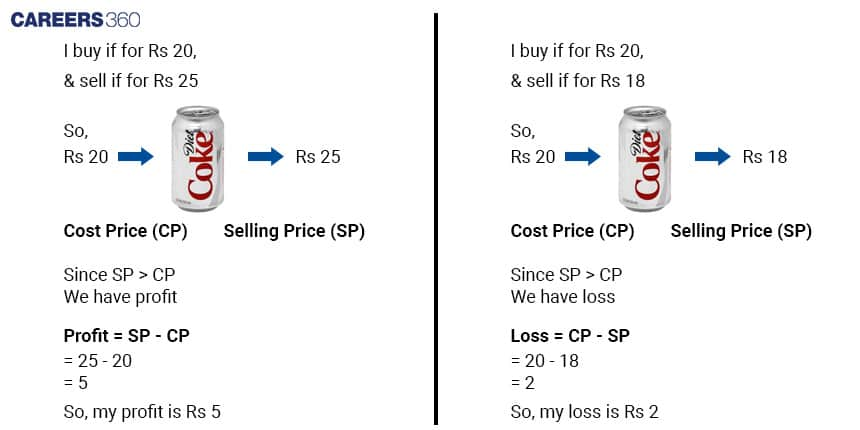
To calculate in percentage use the below formulae

Profit Percentage = (profit/Cost Price)100

Loss Percentage = (Loss/Cost Price)100

Problem 1: A supermarket is offering a bulk discount on apples. For every 4 apples purchased, the customer gets 1 apple for free. If the price of one apple is ₹20, how much would it cost to buy 12 apples?

Solution:

For every 4 apples, 1 apple is free. So, in a set of 4 apples, the customer pays for 3 apples. Cost of 4 apples = 3 * ₹20 = ₹60

To buy 12 apples, we can divide them into sets of 4 apples each. Number of sets of 4 apples = 12 apples ÷ 4 apples/set = 3 sets

Total Cost = Cost of 4 apples * Number of sets Total Cost = ₹60 * 3 = ₹180

Therefore, it would cost ₹180 to buy 12 apples with the bulk discount.

Compound Interest for Better Financial Choices

In CBSE Class 8, students are introduced to the concept of compound interest, which has real-life applications in financial planning. Understanding compound interest empowers students to make informed choices regarding long-term investments and savings.

Compound Interest = Principle [1 + (Interest Rate/100)]^Time - Principle

A = P[1 + r/n)]^nt

Where,

A = final amount

P = Principal amount (initial investment)

r = Annual interest rate (expressed as a decimal)

n = number of times interest is compounded per year

t = number of years

Problem 1: John decides to invest 5,000 in a savings account that pays an annual interest rate of 4%. The interest is compounded annually. Calculate the amount John will have after 5 years.

Solution:

To calculate the amount after 5 years with compound interest, we use the formula

A = P[1 + r/n)]^nt

Given: P = ₹5,000

r = 0.04 (4% as a decimal)

n = 1 (compounded annually)

t = 5 years

Now, substitute the values into the formula:

A = 5000[1 + 0.04/1)]^1*5

A = 5000[1.04]⁵

A = 5000*1.21665

A = 6083.25

After 5 years, John will have approximately ₹6,083.25 in his savings account.

Hope, you have now a good understanding of Comparing Quantities Class 8 which helps you not only in exams but also aids in making informed decisions while in your daily life.