Heron's Formula In Practice: Accurately Determining Area

Heron's Formula is a remarkable mathematical tool for calculating the area of triangles. This formula doesn't rely on the angles of the triangle but is solely dependent on the lengths of its sides. It's an invaluable asset in geometry and trigonometry, offering a precise method for area calculation.

In this comprehensive exploration, we'll dissect Heron's Formula, understand its historical significance, witness its practical applications, explore its adaptability to various types of triangles, and detail its concepts as discussed in Chapter 12 of Class 9 Mathematics by NCERT.

Historical Significance

Heron's Formula bears a rich historical heritage dating back to its originator, Heron of Alexandria, a Greek engineer, and mathematician. Heron formulated this method around 60 CE, using it to calculate triangle areas based solely on side lengths. His contributions extended to proving trigonometric laws, including the Laws of Cosines and the Laws of Cotangents. Heron's work laid the foundation for modern trigonometry and geometry, making his formula a pivotal achievement in the world of mathematics.

Fundamental Components

Heron's Formula deals with triangles, which are defined by their three sides, denoted as 'a', 'b', and 'c'. To apply the formula, we first need to calculate the semi-perimeter, often represented as 's', of the triangle. The semi-perimeter is half of the triangle's perimeter and is computed as:

s = (a + b + c) / 2

With the semi-perimeter (s) in hand, we can proceed to calculate the area (A) of the triangle using Heron's Formula:

A = √(s(s - a)(s - b)(s - c))

This formula elegantly encapsulates the relationship between the sides and area of a triangle. It reveals the beauty of mathematics in its ability to derive precise results from seemingly simple components.

Also Read | Euler's Formula And Topology: A Discussion On Polyhedra

Proof of Heron's Formula for the Area of a Triangle

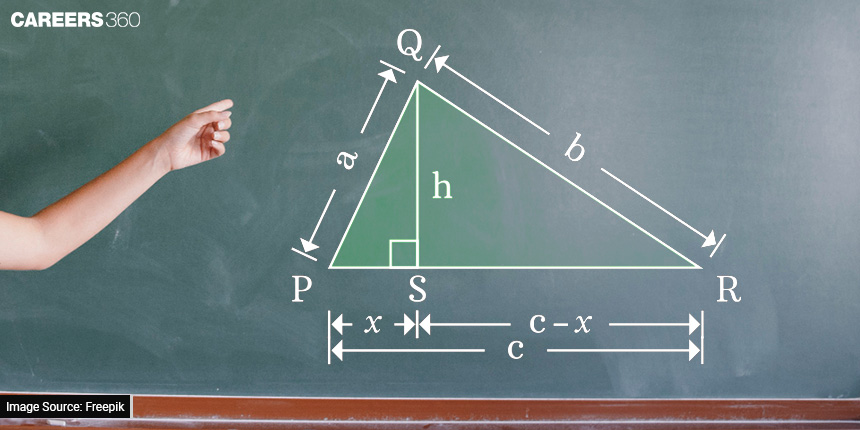
Heron's formula can be derived using Pythagoras' theorem, the formula for the area of a triangle, and algebraic identities. Consider a triangle with sides of length a, b, and c, where the semi-perimeter is denoted as "s," the perimeter as "P," and the area as "A." To illustrate, let's assume that side length b is divided into two segments, p and q, with a perpendicular (h) dropped from vertex B onto side AC at point M. Visualise the triangle below:

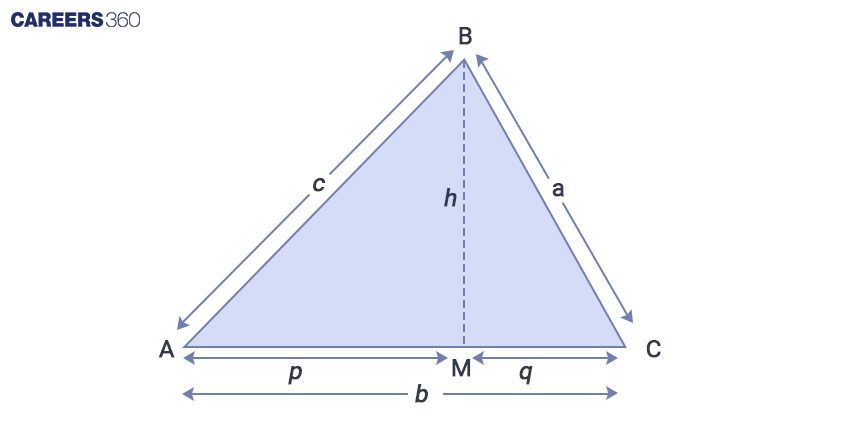
As we know, the area of a triangle is given by (1/2) * base * height, where b represents the base and h is the height of the triangle. Let's begin by calculating the value of h.

From the image, we can express b as the sum of p and q:

⇒ b = p + q ....(1)

Squaring both sides, we obtain:

⇒ q² = b² + p² - 2bp ....(2)

Adding h² to both sides, we get:

q² + h² = b² + p² - 2bp + h² ....(3)

Applying the Pythagoras theorem to triangle BCM, we have:

h² + q² = a² ....(4)

Similarly, applying the Pythagoras theorem to triangle MBA, we get:

p² + h² = c² ....(5)

Substituting the values of (4) and (5) into (3), we obtain:

q² + h² = b² + p² - 2bp + h²

⇒ a² = b² + c² - 2bp

⇒ p = (b² + c² - a²) / (2b) ....(6)

From equation (5), we have:

p² + h² = c²

⇒ h² = c² - p² = (c + p)(c - p) ....(7) (Using the identity a² - b² = (a + b)(a - b))

Substituting (6) into (7), we get:

h² = (c + p)(c - p)

⇒ h² = (c + (b² + c² - a²) / (2b))(c - (b² + c² - a²) / (2b))

⇒ h² = ((2bc + (b² + c² - a²)) / (2b))((2bc - (b² + c² - a²)) / (2b))

⇒ h² = ((b + c)² - a²) / (2b)((a² - (b - c)²) / (2b))

⇒ h² = ((b + c + a)(b + c - a)(a + b - c)(a - b + c)) / (4b²) ....(8) (Using the identity a² - b² = (a + b)(a - b))

Since the perimeter of the triangle is P = a + b + c, and P = 2s (where s is the semi-perimeter, s = P/2), we have:

2s = a + b + c ....(9)

Substituting (9) into (8), we obtain:

h² = ((b + c + a)(b + c - a)(a + b - c)(a - b + c)) / (4b²)

⇒ h² = (2s * (2s - 2a) * (2s - 2b) * (2s - 2c)) / (4b²)

⇒ h = √(4s(s - a)(s - b)(s - c) / b²) ....(10)

The area of triangle ABC is given by A = (1/2) * base * height, which can be expressed as:

A = (1/2) * b * h

A = (1/2) * b * √(4s(s - a)(s - b)(s - c) / b²) (Using equation (10))

A = √(s(s - a)(s - b)(s - c))

Therefore, the area of triangle ABC is A = √(s(s - a)(s - b)(s - c)) square units.

Heron's Formula in Practice

Example 1: Calculating the Area of a Triangle

Let's put Heron's Formula to practical use with an example. Consider a triangle with side lengths of 5 units, 6 units, and 9 units (a = 5, b = 6, c = 9). We aim to find the area of this triangle using Heron's Formula.

Solution:

Calculate the semi-perimeter (s):

s = (a + b + c) / 2 = (5 + 6 + 9) / 2 = 10 units

Apply Heron's Formula:

A = √(s(s - a)(s - b)(s - c)) = √(10(10 - 5)(10 - 6)(10 - 9)) = √(10 * 5 * 4 * 1) = √200 ≈ 14.142 square units

This example illustrates how Heron's Formula enables precise area calculations for triangles, even when dealing with irregular side lengths.

Also Read | How Does Heavy Rainfall Affect The Soil And Animals?

Example 2: Heron's Formula for Quadrilaterals

Heron's Formula isn't confined to triangles; it's a versatile tool for calculating the area of quadrilaterals as well. By dividing a quadrilateral into two triangles and applying Heron's Formula to each, we can determine the total area of the quadrilateral.

Consider a quadrilateral ABCD with side lengths 'a', 'b', 'c', and 'd', along with diagonal 'e' (as depicted in the diagram earlier). To find the area of ABCD, follow these steps:

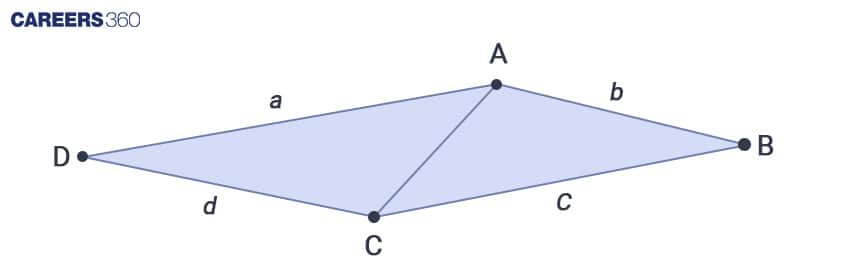
Calculate the semi-perimeters (s₁ and s₂) for the triangles ADC and ABC:

s₁ = (a + d + e) / 2 and s₂ = (b + c + e) / 2

Apply Heron's Formula to find the areas of triangles ADC (A₁) and ABC (A₂):

A₁ = √(s₁(s₁ - a)(s₁ - d)(s₁ - e)) and A₂ = √(s₂(s₂ - b)(s₂ - c)(s₂ - e))

Calculate the total area of quadrilateral ABCD:

Total Area = A₁ + A₂

This approach enables the calculation of the area of irregular quadrilaterals, showcasing Heron's Formula's versatility.

Heron's Formula for Different Types of Triangles

Heron's Formula isn't confined to specific triangle types. Whether you're dealing with equilateral, scalene, or isosceles triangles, Heron's Formula stands as a reliable method for area calculation. Let's explore how Heron's Formula adapts to these different scenarios:

Equilateral Triangle

An equilateral triangle has three equal sides, each of length 'a'. To calculate its area using Heron's Formula, apply the following formula:

Area = (√3 * a²) / 4

This formula elegantly caters to the symmetry of equilateral triangles, making area calculations straightforward.

Scalene Triangle

A scalene triangle has all sides of different lengths ('a', 'b', and 'c'). The application of Heron's Formula to find the area of a scalene triangle involves the standard formula:

Area = √(s(s - a)(s - b)(s - c)), where s = (a + b + c) / 2

Heron's Formula readily handles the complex geometry of scalene triangles, making it an essential tool for area calculations.

Isosceles Triangle

In an isosceles triangle, two sides have equal lengths ('a' and 'b'), while the third side ('c') is distinct. To find the area of an isosceles triangle using Heron's Formula, use the formula below:

Area = (b / 4) * √(4a² - b²)

This formula streamlines Heron's Formula's application to isosceles triangles, offering an efficient solution for area calculations.

Also Read | What Happens To Paper When It Burns? Does It Disappear Or Change Form?

Practical Applications

Heron's Formula finds application in a myriad of real-world scenarios, making it an indispensable tool in various fields:

Architecture and Construction

Architects and engineers rely on Heron's Formula to calculate the areas of irregularly shaped spaces, ensuring precise material estimates for construction projects. From designing rooms with unique layouts to optimising material usage for curved structures, Heron's Formula aids in creating efficient and aesthetically pleasing architectural designs.

Cartography and Geography

In cartography, the science of mapmaking, accurately determining the area of regions and territories is crucial. Heron's Formula allows cartographers to calculate the area of irregularly shaped land masses, providing accurate measurements for maps and geographical studies.

Art and Design

Artists and designers frequently encounter irregular shapes and patterns in their work. Heron's Formula assists in accurately estimating areas for painting, sculpture, and design projects, ensuring that the desired visual impact is achieved.