Non-Euclidean Geometry: Hyperbolic and Spherical Geometry

Geometry is the branch of mathematics that deals with shapes, sizes, and properties of objects and spaces. When we think of geometry, we often picture straight lines, angles, and familiar geometric shapes like squares and circles. This is the world of Euclidean geometry, which most of us learn in school. But what if I told you that there are other kinds of geometry where the rules are different? These alternative geometries, known as non-Euclidean geometries, take us on a journey into worlds where straight lines behave strangely, triangles have surprising angles, and the very nature of space itself is transformed.

Euclidean Geometry: The Geometry We Know

Let's first revisit the geometry we're familiar with. Euclidean geometry, named after the ancient Greek mathematician Euclid, forms the basis of our traditional understanding of space and shapes. It's built on a set of five fundamental rules, or postulates, that describe how points, lines, and shapes interact:

>> Straight Line Segment: You can draw a straight line between any two points.

>> Infinite Extension: Any straight line segment can be extended infinitely in both directions.

>> Circle Construction: Given a point and a distance, you can draw a circle with the point as its centre and the distance as its radius.

>> Right Angles: All right angles, like the corners of a square, are equal to each other.

>> Parallel Postulate: If two lines are drawn that intersect a third line in such a way that the sum of the inner angles on one side is less than two right angles, then those two lines will eventually intersect on that side.

These postulates serve as the building blocks of Euclidean geometry, guiding our understanding of the world in terms of flat, two-dimensional space and the three-dimensional space we live in.

Non-Euclidean Geometry: A Departure from the Norm

Non-Euclidean geometries emerged in the 19th century when mathematicians began to question the fifth postulate of Euclidean geometry, also known as the parallel postulate. This postulate asserts that given a line and a point not on that line, there is exactly one line parallel to the given line passing through the given point. However, attempts to prove this postulate led to paradoxes and contradictions, pushing mathematicians to explore alternative geometric systems.

Hyperbolic Geometry: The World of Infinite Choices

One of the alternative geometries that emerged is hyperbolic geometry. Mathematicians such as Carl Friedrich Gauss, Nikolai Lobachevsky, and János Bolyai independently developed hyperbolic geometry. In this geometry, a fundamental change is made to the parallel postulate:

>> Revised Parallel Postulate for Hyperbolic Geometry: Through a given point not on a given line, there are infinitely many lines parallel to the given line.

This change creates a space where parallel lines behave differently from what we're used to in Euclidean geometry. Instead of having just one parallel line, you can have countless parallel lines, and this has some fascinating consequences.

Solved Problem 1: Finding the Angle Sum in a Hyperbolic Triangle

In hyperbolic geometry, the angles of a triangle add up to less than 180 degrees, which is different from Euclidean geometry where they always add up to 180 degrees. Let's say we have a hyperbolic triangle with angles A, B, and C. We can use the formula for the angle sum:

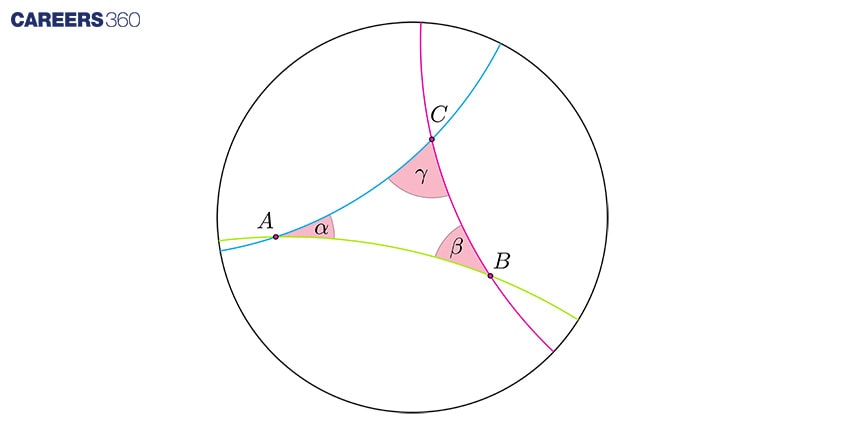
Angle Sum (A + B + C) < 180 degrees

Suppose angles A = 60 degrees and B = 70 degrees. To find the third angle C:

Angle Sum (60 + 70 + C) < 180 130 + C < 180

Solving for C:

C < 180 - 130 C < 50

So, in hyperbolic geometry, the third angle C must be less than 50 degrees for the triangle to be valid.

Formula 1: Hyperbolic Distance

In hyperbolic geometry, distance is measured differently than in Euclidean space. The hyperbolic distance (δ) between two points with coordinates (x₁, y₁) and (x₂, y₂) on the hyperbolic plane is given by:

δ = cosh⁻¹(cosh(x₁ - x₂) ⋅ cosh(y₁ - y₂))

Here, cosh represents the hyperbolic cosine function.

Spherical Geometry: The Curvature of the Cosmos

On the other hand, spherical geometry explores spaces with positive curvature, just like the surface of a sphere. This geometry is particularly relevant to fields like astronomy and geography, where the Earth's surface is considered as a sphere.

Properties of Spherical Geometry

>> Positive Curvature: Spherical surfaces curve toward each other, much like the surface of a ball. This positive curvature is different from the flat surfaces of Euclidean geometry.

>> Shortest Paths: In spherical geometry, the shortest path between two points is an arc of a great circle. A great circle is the largest circle that can be drawn on a sphere, and it plays a crucial role in navigation.

>> Angle Excess: Unlike Euclidean and hyperbolic geometry, where the angles of a triangle always add up to a fixed value (180 degrees in Euclidean and less than 180 degrees in hyperbolic), the angles of a spherical triangle always add up to more than 180 degrees.

Also check - What Causes Preserved Food To Get Contaminated?

Solved Problem 2: Navigating on a Sphere

Imagine you're sailing on Earth, and you want to find the shortest distance between two cities along the surface. You have a globe with a radius (R) of 6371 kilometres (which is roughly the Earth's radius). The coordinates of the two cities are City A (latitude 40° N, longitude 70° W) and City B (latitude 35° N, longitude 85° W). What is the shortest distance between these two cities along the surface of the Earth?

To find the shortest distance, we use spherical geometry, which tells us that the shortest path between two points on a sphere is an arc of a great circle. In this case, the great circle connecting City A and City B is the same as the circle of latitude at 40° N.

Now, we need to find the central angle (θ) between City A and City B. The difference in longitudes between the cities is 70° W - 85° W = 15° in the westward direction. To convert this into a central angle, we use the formula:

θ = (Longitude Difference / 360°) * 2π

Substituting the values:

θ = (15° / 360°) * 2π

θ = (1/24) * 2π

θ = π/12

Now, we can find the length of the arc along the sphere's surface:

Length (L) = Radius (R) * θ

Substituting the radius (R = 6371 kilometres) and θ = π/12:

Length (L) = 6371 * (π/12)

Length (L) ≈ 1672.48 kilometres

So, the shortest distance between City A and City B along the surface of the Earth is approximately 1672.48 kilometres.

Formula 2: Spherical Law of Cosines

The spherical law of cosines relates the sides and angles of a spherical triangle. For a spherical triangle with sides (a, b, c) and opposite angles (A, B, C) respectively, the formula is:

cos(c) = cos(a) * cos(b) + sin(a) * sin(b) * cos(C)

Where:

cos(c) is the cosine of side c,

cos(a) and cos(b) are the cosines of sides a and b,

sin(a) and sin(b) are the sines of sides a and b,

cos(C) is the cosine of angle C.

Also check - What Is The Role Of Capacitors In Electronic Devices?

Practical Applications of Non-Euclidean Geometry

Non-Euclidean geometries, particularly hyperbolic and spherical geometries, might seem like abstract mathematical concepts, but they have found surprising and practical applications in various fields.

Hyperbolic Geometry in Art and Design

The unique visual properties of hyperbolic geometry have inspired artists and designers. One of the most famous artists who incorporated hyperbolic patterns into his work is M.C. Escher. His intricate and mind-bending designs often featured hyperbolic tessellations, where shapes repeat infinitely.

Hyperbolic Geometry in Physics

Hyperbolic geometry plays a role in our understanding of the curvature of spacetime in Einstein's theory of general relativity. In this theory, gravity is described as the curvature of spacetime caused by mass and energy, and hyperbolic geometry contributes to the mathematical framework that describes this curvature.

Hyperbolic Geometry in Computer Graphics

In the world of computer graphics, algorithms based on hyperbolic geometry are used to create 3D scenes on flat computer screens. These algorithms help simulate realistic environments, enabling the development of video games, simulations, and virtual reality experiences.

Spherical Geometry in Navigation

Spherical geometry is essential for navigation on Earth's surface. When you want to find the shortest distance between two locations on Earth, you use the principles of spherical geometry to calculate it. Navigational instruments like sextants and GPS systems rely on spherical geometry to determine positions accurately.