Crucial Concepts For Exams: Understanding Pipes And Cisterns

Understanding pipes and cisterns goes way beyond everyday use. They’re crucial in maths tests, asking how fast water flows or how long to fill a tank. From middle school to high school, these concepts pop up in different parts of maths and science, making it easier to understand and solve problems, especially in exams.

Knowing about pipes and cisterns isn’t just for school—it’s super handy in jobs like engineering or management. It helps handle water-related issues and saves water too. In exams, questions about them are a big deal, often getting good marks. Figuring out how long it takes to fill or empty a cistern using different pipes is key.

These ideas are everywhere in exams, not just in school but in jobs like banking, SSC, RRB, and insurance tests. So, taking time to understand pipes and cisterns is important if you want to do well in these tests. Here in this article we comprehensively discuss concepts of pipe and cisterns including formulae, tricks, and solved problems based on daily issues.

Formulae and Concepts of Pipe and Cisterns

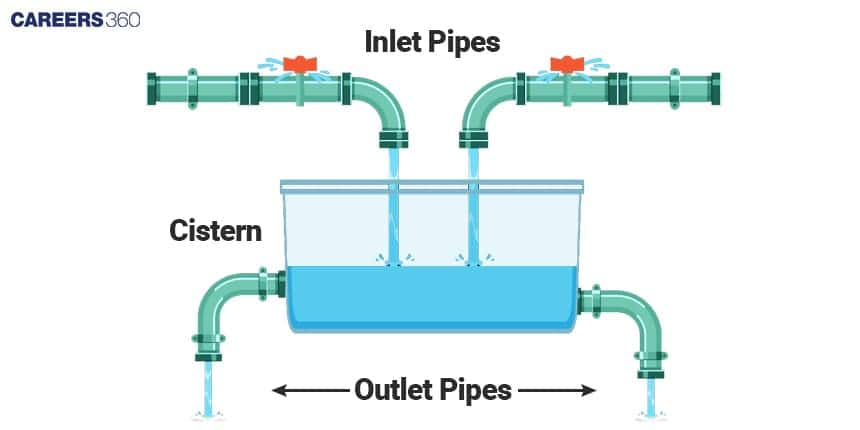
These concepts revolve around the flow of liquids, focusing on inlet and outlet pipes connected to a container, often referred to as a cistern or tank.

Key Components:

>> Inlet Pipe: The pipe responsible for filling the cistern or tank is termed the inlet. It's associated with positive work, adding liquid to the container.

>> Outlet Pipe: The pipe that empties the cistern is the outlet. It's linked with negative work, draining liquid from the container.

Fundamental Formulas:

>> Filling a Tank: If x hours are required to fill the tank, the part filled in 1 hour = 1/x.

>> Emptying a Tank: If y hours are required to empty the tank, the part emptied in 1 hour = 1/y.

Combined Pipe Operations:

When both an inlet and an outlet are operational:

If a pipe can fill a tank in x hours and empty the same tank in y hours:

• Net part of the tank filled in 1 hour = {(xy) / (y-x)} .... (y > x)

• Net part of the tank filled in 1 hour = {(xy) / (x-y)} .... (x > y)

Net Work Done: Net work done = (Sum of work done by Inlets) – (Sum of work done by Outlets).

Multiple Inlets:

If two inlets fill a tank in x and y hours respectively:

Time taken when both inlets are open = 1/{1/x + 1/y} = xy/(x + y).

Inlets and Outlet:

If two pipes take x and y hours to fill a tank and a third pipe empties it in z hours:

• Time taken to fill the tank = 1 / {(1/x) + (1/y) - (1/z)}.

• Net part of the tank filled in 1 hour = (1/x) + (1/y) - (1/z).

Work done = Time taken * Rate of work

Part of the cistern filled/emptied in 1 hour = 1 / Time taken

Problem Solving Methods

There are many methods including Unitary method and LCM method that are discussed below.

>> Unitary Method Using Formulas: Apply formulas directly based on the given conditions.

In this method, we use 1 as the total work amount, figure out how efficient each pipe is in parts, and solve the problem step by step.

Let's use this method to solve a problem:

Example:

There are three pipes—A, B, and C. A fills a tank in 30 hours, B in 40 hours, and C empties it in 20 hours. If all three are open together, how long will it take to fill the tank?

Step 1: Imagine the total work as 1.

Step 2: Find out how much each pipe does in an hour.

Pipe A fills 1/30th of the tank in 1 hour.

Pipe B fills 1/40th of the tank in 1 hour.

Pipe C empties 1/20th of the tank in 1 hour.

Step 3: Calculate how much work they do together in an hour.

130 + 140 - 120 = (4 + 3 - 6)/120 = 1/120

It turns out that together, they do 1/120th of the work in 1 hour.

Step 4: To find out how long it takes to fill the tank, we take the inverse of the work done in 1 hour.

So, the tank will be filled in 120 hours

>> LCM Method: Determine the rates of each pipe, find the combined rate, and calculate the time required for a specified quantity.

In this approach, we use the least common multiple (LCM) of the given numbers as the total work, figure out how much each pipe does in whole numbers, and solve the problem efficiently.

Let's solve an example problem:

Pipes A and B can fill a tank in 30 and 40 hours respectively, while Pipe C can empty it in 20 hours. If all three pipes are opened together, how long will it take to fill the tank?

Step 1: Assume the total work as the LCM of 30, 40, and 20, which is 120.

Step 2: Find how much work each pipe does in 1 hour using this total work.

Pipe A does 4 units of work in 1 hour (120 work in 30 hours).

Pipe B does 3 units of work in 1 hour (120 work in 40 hours).

Pipe C takes away 6 units of work in 1 hour (120 work in 20 hours).

Step 3: Calculate how much work they do together in 1 hour.

4 + 3 - 6 = 1

Together, they do 1 unit of work in 1 hour.

Step 4: Divide the total work by the work done in 1 hour, which gives us 120/1, resulting in 120 hours to fill the tank

Also check - What Are Exponential And Logarithmic Functions, And How Do They Work?

Solved Problem

Delving into solved problems offers a practical lens through which to comprehend these concepts thoroughly. By witnessing the application of these principles in real-life scenarios, a deeper understanding ensues.

Problem: Two pipes, A and B, can fill a tank by themselves in 20 and 30 minutes, respectively. If both pipes are turned on together, how long will it take to fill the tank completely?

(a) 10 minutes (b) 12 minutes (c) 15 minutes (d) 25 minutes

Solution:

Given that Pipe A can fill tank in 20 minutes

Pipe B can fill a tank in 30 minutes

Find out: how much time both pipes take to fill this tank.

Unitary Method

Work done by A in one minute = 1/20 units

Work done by B in one minute = 1/ 30 units

Work done by both in one minute = 1/20 + 1/30 units

= (3 + 2)/60

= 5/60

1/12 units

Time taken to fill the tank by both pipes = 1/(1/12) = 12 minutes

Hence, option b) 12 minutes is correct.

LCM Method

Assume total work = LCM(20, 30) = 60 units.

Work done by A in one minute = 60/20 = 3 units

Work done by B in one minutes = 60/30 = 2 units

Work done by both in one minutes = 3 + 2 = 5 units

Time take to complete 60 units of work = 60/5 = 12 minutes

Problem: A drain pipe that drains a tank needs 12 hours, while a filling pipe can do it in 6 hours. If a total of 'n' pipes, some filling and the rest draining, work together, they can fill the tank in 2 hours. How many following different values could 'n' be? {24, 16, 33, 13, 9, 8}

Solution:

Given that

Drain pipe drains tank in 12 hr

Filling pipe fills tank in 6hr

Total n pipe, some filling and rest are draining, fill the tank in 2 hr

Find: value of n

Unitary Method

Work done by drain pipe in 1 hr = 1/12

Work done by fill pipe in 1 hr = 1/6

Let x are filling pipe, so draining pipe = n - x

Work done by n pipe in 1 hr = x(1/6) - (n - x)(1/12)

x/6 - n/12 + x/12 = (2x - n + x)/12

Time taken to fill the tank = 12/(3x - n) = 2

3x - n = 6

n = 3x - 6

For x = 1, n = -3

x = 2, n = 0

x = 3, n = 3

x = 4, n = 6

x = 5, n = 9

x = 6, n = 12

We can observe that the value of n can be 0, 3, 6, 9, 12, 15, 18…

Multiple of three therefore values (9, 24, 33 can be possible)

LCM Method

Suppose total work = LCM(6,12) = 12

Work done by drain pipe in 1 h r= 12/12 = 1 unit

Work done by filling pipe in 1 hr = 12/6 = 2 unit

Let x are filling pipe, so draining pipe = n - x

Total work done by both in 1 hr = 2x - 1(n - x) = (3x - n) unit

Time taken to fill the tank = 12/(3x - n) = 2

3x - n = 6

n = 3 (x - 2)

Therefore the value of n can be multiple of 3, possible values are 9, 24, 33.

Effective Problem Solving Strategies

>> Familiarity with Terminology: Familiarising yourself with crucial terms such as inlet, outlet, pipe, cisterns, and leak is vital. Understanding them helps in deciphering the roles of different elements and how they affect the overall situation.

>> Practice and Memorisation: Consistent practice and committing formulas to memory are fundamental. The more you practise solving problems involving pipes and cisterns, the better you'll become at applying the right formulas and methods. Memorising these formulas aids in quick recall during exams or problem-solving sessions, enabling faster and accurate solutions.

Also check - Asexual Reproduction In Animals: Exploring Parthenogenesis And Budding

Hope this helps you to understand the mathematics of Pipe and Cisterns concepts such as unitary method, LCM method, and how these concepts can be applied in real life issues.