Permutation And Combinations: It Is Not Just A Game Of Choice, But A Well Calculated Effort

Permutations and combinations are like solving puzzles by arranging things in different ways. They might seem a bit tough, but they're super helpful, especially for students in Class 12. These ideas aren't just for tests; they're for solving real problems we face every day.

Imagine you're figuring out a game or solving a tricky puzzle—knowing about permutations and combinations is like having a secret code to solve these challenges. These maths tools help to solve tough problems, understand how likely things are in games, or even find patterns in things like passwords or how traits pass on in families.

This article is here to make these maths ideas easier to understand. It's like a helpful guide that shows how to use these ideas in real life. In school, these ideas are part of the books from NCERT. In Class 11, you start learning the basics about arranging and choosing things in certain ways. Then, in Class 12, it gets more interesting, showing how these ideas connect to different parts of science or technology. This article is like an extra tool to understand and use what's in those textbooks, making it easier to see why these maths ideas are important and how they help us in our daily lives.

What is Permutation and combination?

>> Permutations: It's like lining up things in a specific order. Imagine arranging toys on a shelf in a particular sequence. The way you arrange them matters.

>> Combinations: This is more about picking things without caring about the order. It's like choosing a group of friends to play with, where who you pick matters, not the order you pick them in.

Sum Rule

Performing Tasks Together (Connected by 'AND'): When you do two tasks in a row, like eating breakfast and then brushing your teeth, you have to find the total ways by multiplying how many choices you have for each task.

Product Rule

Performing Either Task (Connected by 'OR'): If you're doing only one of two tasks, like choosing between eating breakfast or lunch, you have to find the total ways by adding the number of ways for each task.

For example examples, In a shop with 'd' doors and 'w' windows:

If a thief wants to enter through either a door or a window, they can do it in (d + w) ways.

If the thief enters through a door and leaves through a window, they can do it in (d × w) ways by multiplying the number of doors and windows.

Also Read | Learn To Solve Maths Alligation And Mixtures Problems like A Pro

Arrangement And Related Concepts

Linear arrangement of 'r' out of 'n' distinct items (nPr):

nPr = n × (n - 1) × (n - 2) × ... × (n - r + 1) = n! / (n - r)!

Circular arrangement of 'n' distinct items:

For 'n' items arranged in a circle, fix one item and arrange the rest linearly, resulting in (n - 1)! ways.

Selection of 'r' items out of 'n' distinct items (nCr):

nCr = nPr / r! = n! / (r! × (n - r)!)

Arranging identical items:

Formula: Number of ways to arrange 'n' items where 'p' are alike, 'q' are alike, 'r' are alike, etc.:

n! / (p! × q! × r! × ...)

Solved Problems

Let's have fun figuring out how to put things in different orders! We'll solve puzzles that help us see all the different ways things can be arranged.

Question 1: How many ways can we make a flag with 4 horizontal stripes using red, green, and yellow, without having two stripes of the same colour next to each other?

Solution:

There are four horizontal stripes and three colour choices: red, green and Yellow.

Also Read | Is There A Maths Shortcut For Stock Market Success?

Let's see how many ways we can make a flag using different colours for each strip.

For the first strip, we can pick from three colours: red, green, or yellow.

Then, for the next strip, we have two choices because we can't use the same colour as the one beside it.

For the next two strips, C and D, we also have two options each because we can't use the same colour as the one next to it. So, multiplying all the choices together gives us a total of 24 ways to make the flag.

Question 2: A password consists of 5 characters using letters and digits. How many different passwords are possible if repetition of characters is allowed?

Solutions:

There are 26 letters and 10 digits, meaning a total of 36 choices are available for one character.

Here repetition is allowed.

Hence total number of ways in which a password can be generated

36^5

Question 3: A group of 7 people includes 4 mathematicians and 3 physicists. In how many ways can a committee of 3 people be formed such that there is at least 1 mathematician?

Solution:

Total ways to choose 3 people C(7,3) = 35

Ways to choose all physicists = 1.

Therefore, ways to have at least 1 mathematician: 35−1 = 34.

Question 4: Imagine A, B, and C are three spots. There are 3 roads from A to B, 4 roads from B to C, and 3 roads from A to C. How many ways can someone go from A to C using these roads?

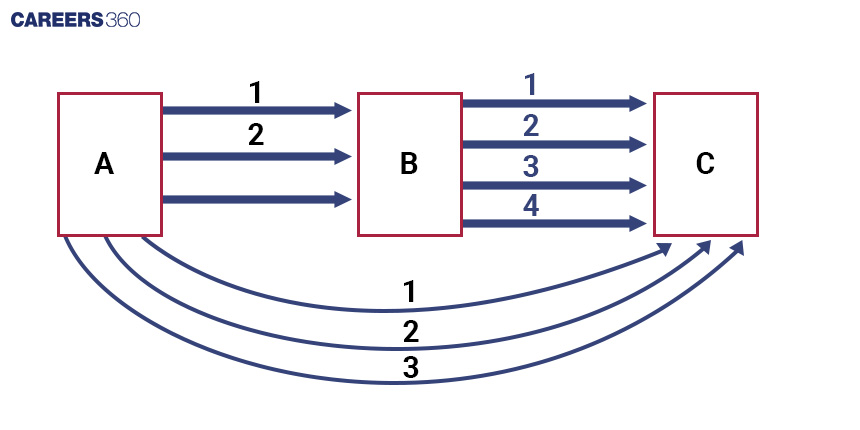
Solution:

First, we try going from A to B, then B to C. We use product rules. That's 3 roads from A to B times 4 roads from B to C, which gives us 12 ways.

Next, we think about taking the direct road from A to C, which gives us 3 ways. Now, we use the sum rule. We add the 12 ways we found earlier to the 3 ways from A to C directly. That's 12 plus 3, which gives us a total of 15 ways to reach spot C from A.

Hope this helps you better understand concepts such as permutation, combinations, sum rule, product rule and how to tackle problems connected to these ideas.