Mathematical Tools In Thermodynamics: Understanding Heat And Energy Transfer

Thermodynamics, as a branch of physics, deals with the study of energy and its transformations in various systems. It provides the foundation for understanding and analysing the behaviour of matter and energy in a wide range of phenomena, from the behaviour of gases to the operation of heat engines. One of the crucial aspects of thermodynamics is the study of heat and energy transfer, which allows us to comprehend the fundamental processes underlying the functioning of our physical world.

This Story also Contains

1. Basic Concepts Of Thermodynamics
2. Laws Of Thermodynamics
3. Mathematical Tools For Quantifying Heat And Energy Transfer
4. Laws Of Heat Transfer

To delve into the intricacies of heat and energy transfer, mathematical tools play a vital role in providing a systematic framework for analysis and prediction. By utilising mathematical techniques, such as calculus, differential equations, and statistical methods, we can gain profound insights into the behaviour of thermodynamic systems, enabling us to make accurate predictions and design efficient energy systems.

This article aims to explore the basics of thermodynamics such as concepts of energy, heat, specific heat, latent heat, and temperature, the fundamental mathematical tools employed in thermodynamics, and their significance in comprehending heat and energy transfer processes.

Also check - Chemical Kinetics: Mathematical Modeling Of Reaction Rates

Basic Concepts Of Thermodynamics

Latent Heat

Latent heat is the heat energy absorbed or released during a phase change of a substance, without a change in its temperature. It is classified into two types: latent heat of fusion and latent heat of evaporation.

>> Latent Heat of Fusion: The latent heat of fusion is the amount of heat energy required to change a substance from a solid to a liquid state, or vice versa, at a constant temperature. Let's take an example to understand this concept better.

Imagine we have an ice cube at 0 degrees Celsius. To melt this ice cube, we need to provide heat energy. The amount of heat energy required is given by the formula:

Q = mL

Where:

• Q = Heat energy absorbed or released (in Joules)

• m = Mass of the substance (in kilograms)

• L = Latent heat of fusion (in Joules per kilogram)

For water, the latent heat of fusion is approximately 334,000 J/kg. So, if we have a 1 kg ice cube, the amount of heat energy required to melt it completely would be 334,000 J.

>> Latent Heat of Evaporation: The latent heat of evaporation is the amount of heat energy required to change a substance from a liquid to a gas state, or vice versa, at a constant temperature. Let's consider an example to understand this concept.

Suppose we have water at 100 degrees Celsius and we want to convert it into steam. To achieve this, we need to provide heat energy. The amount of heat energy required is given by the formula:

Q = mL

Where:

• Q = Heat energy absorbed or released (in Joules)

• m = Mass of the substance (in kilograms)

• L = Latent heat of evaporation (in Joules per kilogram)

For water, the latent heat of evaporation is approximately 2,260,000 J/kg. So, if we have 1 kg of water, the amount of heat energy required to completely evaporate it would be 2,260,000 J.

Specific Heat

Specific heat is the amount of heat energy required to raise the temperature of a substance by a certain amount. Different substances have different specific heat capacities, which are measured in Joules per kilogram per degree Celsius (J/kg°C).

The formula to calculate the heat energy using specific heat is:

Q = mcΔT

Where:

• Q = Heat energy absorbed or released (in Joules)

• m = Mass of the substance (in kilograms)

• c = Specific heat capacity (in J/kg°C)

• ΔT = Change in temperature (in degrees Celsius)

For example, let's consider a 2 kg block of iron with a specific heat capacity of approximately 450 J/kg°C. If the temperature of the iron block increases by 10 degrees Celsius, the amount of heat energy absorbed or released can be calculated using the formula above.

Q = mcΔT

Q = (2 kg) × (450 J/kg°C) × (10°C) Q

Q = 9,000 J

So, a 2 kg block of iron would absorb or release 9,000 Joules of heat energy when its temperature changes by 10 degrees Celsius.

Laws Of Thermodynamics

The laws of thermodynamics govern the behaviour of energy in various systems. Let's explore two important laws: the first law of thermodynamics and Newton's law of cooling.

Zeroth Law

The Zeroth Law states that if two objects are in thermal equilibrium with a third object, they are also in equilibrium with each other. This law establishes the concept of temperature and the basis for temperature measurements.

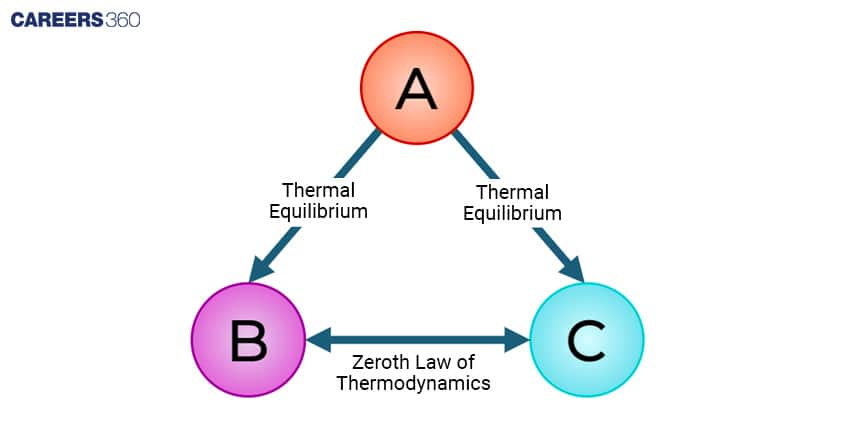
Mathematically, the Zeroth Law can be represented as If object A is in thermal equilibrium with object C, and object A is also in thermal equilibrium with object B, then object B and object C are in thermal equilibrium with each other.

First Law of Thermodynamics

The first law of thermodynamics states that energy cannot be created or destroyed; it can only be transferred or transformed from one form to another. This law is also known as the law of conservation of energy. It can be expressed mathematically as:

ΔU = Q - W

Where:

• ΔU = Change in internal energy of the system

• Q = Heat energy absorbed or released by the system

• W = Work done by the system

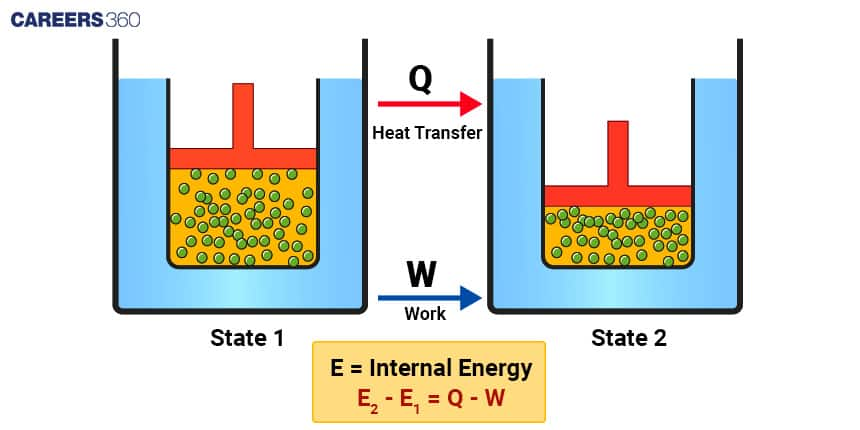
This equation indicates that the change in internal energy (E2 -E1) of a system is equal to the heat energy absorbed or released by the system minus the work done by the system.

Consider A gas undergoes a thermodynamic process described by the equation

PV² = constant, where P is the pressure and V is the volume. During this process, the volume changes with time according to V(t) = 3t², where t is the time in seconds. Calculate the rate of change of the internal energy of the gas with respect to time.

Solution:

We know that the first law of thermodynamics

ΔU = Q - W

Given that

PV² = constant

differentiate both sides of the equation

P2VdV/dt = 0, substituting V(t) = 3t²

6Pt²dV/dt = 0 dVdt = 0, Therefore work done =0

Since no information of heat is given so we assume that change in Q = 0

Thus ΔU = 0

Second Law of Thermodynamics

The Second Law encompasses several principles related to the direction and efficiency of heat transfer. One important concept in the Second Law is entropy (S), which measures the disorder or randomness in a system.

Mathematically, the Second Law can be stated as:

ΔS ≥ Q/T

Where:

• ΔS = Change in entropy

• Q = Heat transferred

• T = Absolute temperature

Mathematical Tools For Quantifying Heat And Energy Transfer

Here, we explore some of the key mathematical techniques used in thermodynamics

>> Differential Calculus: Differential calculus plays a significant role in thermodynamics by allowing us to express and analyse rates of change. Differential equations, a cornerstone of differential calculus, help describe how thermodynamic variables, such as temperature, pressure, and volume, change with respect to one another. These equations enable us to understand the dynamic behaviour of thermodynamic systems and make predictions about their future states.

>> Integral Calculus: Integral calculus complements differential calculus in thermodynamics by providing tools to calculate cumulative quantities and perform energy balance analyses. Integrating thermodynamic properties over a given range allows us to determine quantities such as heat transfer, work done, and changes in energy. These integrals aid in quantifying the flow and transformation of energy within a system.

Laws Of Heat Transfer

Stefan-Boltzmann's Law (Thermal Radiation):

Stefan-Boltzmann's Law quantifies the total amount of thermal radiation emitted by a black body. It states that the total power (P) radiated per unit surface area is proportional to the fourth power of the absolute temperature (T) of the object.

Mathematically, Stefan-Boltzmann's Law can be expressed as:

P = σAT⁴

Where:

• P = Total power radiated

• σ = Stefan-Boltzmann constant,

• A = Surface area

• T = Absolute temperature.

Newton's Law of Cooling

Newton's law of cooling describes the rate at which an object cools or heats when placed in contact with a medium at a different temperature. According to this law, the rate of change of temperature of an object is directly proportional to the temperature difference between the object and its surroundings. Mathematically, it can be expressed as:

dT/dt = -k(T - Ts)

Where:

• dT/dt = Rate of change of temperature with respect to time

• k = Cooling constant (depends on the nature of the object and the medium)

• T = Temperature of the object

• Ts = Temperature of the surroundings

To find the solution, we rearrange the equation as follows:

dT / (T - Ts) = -k dt

Next, we integrate both sides of the equation:

∫ dT / (T - Ts) = -k ∫ dt

To simplify the integration on the left-hand side, we use the substitution u = T - Ts, which implies du = dT:

∫ du / u = -k ∫ dt

Applying the integral on both sides, we get:

ln|u| = -kt + C

Here, C is the constant of integration. Substituting back u = T - Ts, we have:

ln|T - Ts| = -kt + C

To find the value of the constant C, we use the initial condition T = T0 at t = 0:

ln|T0 - Ts| = -k(0) + C

ln|T0 - Ta| = C

Substituting C back into the equation, we obtain:

ln|T - Ts| = -kt + ln|T0 - Ta|

Exponentiating both sides gives:

|T - Ts| = |T0 - Ts| * e(-kt)

Since the exponential term e^(-kt) is always positive, we can remove the absolute value signs:

T - Ts = (T0 - Ts) * e(-kt)

Finally, isolating T, we get the final form of Newton's Law of Cooling:

T = Ts + (T0 - Ts) * e(-kt)

Example: Let's consider a cup of hot coffee with an initial temperature of 90 degrees Celsius, placed in a room with a temperature of 20 degrees Celsius. The cooling constant, k, is determined by the properties of the cup and coffee.

Solution:

If the rate of change of temperature is given as -2 degrees Celsius per minute, we can use Newton's law of cooling to find the value of k:

-2 = k(90 - 20)

-2 = 70k

k = -2/70

k ≈ -0.0286

By substituting the obtained value of k and the given temperatures into the equation, we can calculate the time it takes for the coffee to cool down to a certain temperature.

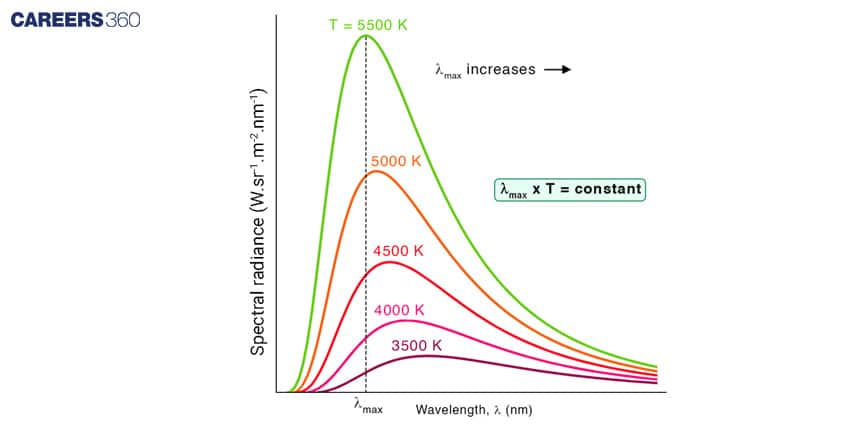
Wien's Law

Wien's Law establishes the relationship between the peak wavelength (λ_max) of the radiation emitted by a black body and its absolute temperature (T). It states that the product of the peak wavelength and the absolute temperature is constant.

Mathematically, Wien's Law is given by:

λ_max T = b

where:

• λmax = peak wavelength

• T = Absolute temperature

• b = Wien displacement constant

Now, You have a basic idea of how mathematical tools and concepts play a crucial role in understanding thermodynamics and transfer of heat.

Also check - Chronic Inflammation: Causes And Solution To Eliminate Pain