Mathematical Principles Behind Geographic Information Systems (GIS)

Geographic Information Systems, or GIS are computer-based tools that allow us to collect, store, analyse, and visualise spatial data. They have become an essential part of modern-day decision-making in a wide range of fields, from urban planning and natural resource management to emergency response and public health.

But what are the mathematical principles that make GIS work? In simple terms, GIS is built on a foundation of geometry, trigonometry, and calculus. Geometry is used to represent the shape, size, and location of geographic features such as roads, buildings, and rivers. Trigonometry is used to calculate distances, angles, and elevations between these features, while calculus is used to model and analyse complex spatial phenomena such as water flow, land use change, and population growth.

Beyond these foundational principles, GIS also relies on a range of statistical and computational techniques such as clustering, regression analysis, and machine learning. These tools allow GIS users to uncover patterns and trends in spatial data, make predictions about future events, and optimise decision-making in real-time.

As a Class 12 student, learning GIS is important not just for subjects like geography, environmental science, and agriculture that are relevant for the board and competitive exams like SSC CGL, State PCS, and UPSC, but also for future careers in fields like business and marketing where understanding of demographics trends is crucial. This article will explain how GIS works, the mathematical principle behind GIS, how it is used in real life, and what difficulties come up when working with spatial data.

How Does GIS Work?

Geographic Information Systems (GIS) is a system designed to capture, store, manipulate, analyse, manage, and present spatial or geographic data. GIS technology combines various types of data such as maps, satellite imagery, aerial photography, and geographic data from various sources to provide a comprehensive view of a location or region. It helps in visualising, interpreting, and understanding patterns and relationships in data that can be used in making informed decisions about a particular location or area.

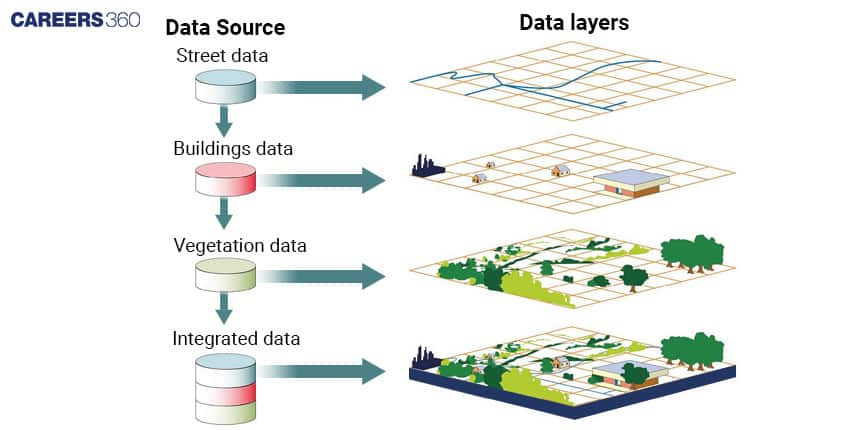
Mathematical Principles Behind GIS

GIS is built on a foundation of several mathematical principles that enable the manipulation, analysis, and representation of spatial data. The three key mathematical concepts that underlie GIS are geometry, trigonometry, and calculus.

Geometry

It is the branch of mathematics that deals with the properties and relationships of points, lines, angles, surfaces, and solids in space. In GIS, geometry is used to represent the shape, size, and location of geographic features such as roads, buildings, and rivers. For example, the geometry of a river can be represented as a series of interconnected points that define its path, while the geometry of a building can be represented as a series of points, lines, and polygons that define its shape and location.

Also check - What Is More Important, What Do You Eat Or How Much You Eat?

Trigonometry

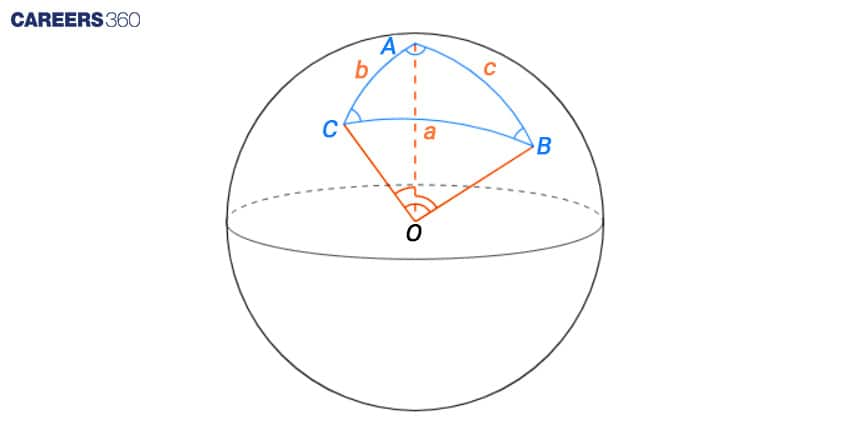
It is the branch of mathematics that deals with the relationships between the sides and angles of triangles. In GIS, trigonometry is used to calculate distances, angles, and elevations between geographic features. For example, trigonometry can be used to calculate the distance between two points on a map, or the angle of inclination of a hill slope. Trigonometric functions such as sine, cosine, and tangent are commonly used in GIS to calculate spatial relationships as shown in the following image A, B, C are three cities.

Let's say we want to calculate the distance between two points. We can use the distance formula from Euclidean geometry, which is:

Distance = √{(x₂-x₁)²+(y₂-y₁)²}

In this formula, (x₂,x₁) and (y₂,y₁) represent the coordinates of the two points. Let's say the coordinates of the two points are (10, 20) and (30, 40). We can calculate the distance between these two points as follows:

Distance = √{(30-10)²+(40-20)²}

Distance =√(400+400)

Distance = √800

Distance = 28.28 units

Calculus

It is the branch of mathematics that deals with the study of rates of change and accumulation. In GIS, calculus is used to model and analyse complex spatial phenomena such as water flow, land use change, and population growth. For example, calculus can be used to model the flow of water through a river network, or to analyse the rate of change of land use in a region. Calculus is also used in spatial interpolation, which is the process of estimating unknown values at locations within a set of known values.

Applications Of GIS

GIS is used in multiple areas such as Environmental Management to monitor and manage natural resources, such as forests, wetlands, and water bodies. Emergency Management to prepare for and respond to natural disasters such as hurricanes, earthquakes, and wildfires. Agriculture to analyse soil type, weather patterns, and crop yield data to make informed decisions about crop management. GIS can help farmers identify the best areas for planting crops, optimise irrigation systems, and monitor crop growth and health. Health Care to analyse and visualise health care data, such as disease outbreaks and demographic information, to identify trends and patterns.

Challenges

• Data Quality: The accuracy and quality of the data used in GIS can have a major impact on the reliability of the analysis and decision-making process. GIS data often comes from different sources and formats, and may not be up-to-date or complete. Ensuring the accuracy and reliability of the data used in GIS requires careful attention to data collection, management, and quality control.

• Data Integration: GIS technology can integrate data from various sources, but integrating data from different sources can be complex and time-consuming. Different data formats, projection systems, and data standards can create compatibility issues that need to be addressed.

• Cost: GIS software and hardware can be expensive, and the costs associated with acquiring, managing, and updating spatial data can be significant. Smaller organisations may find it difficult to justify the cost of GIS, and may need to seek funding from outside sources.

Also check - What Do You Need You To Know To Prevent Electric Scooter Fires?