Understanding Integration: The Power Of Substitution Method

In maths, there's this thing called integration. Some integrations are easy to figure out, while others are difficult. But here's the cool part: this special concept called 'substitution' helps crack those tough integrals. Substitution is like swapping things in an integration to make it easier to solve. It's not just about doing maths; substitution is a smart way to simplify hard integrals. It's like having a secret strategy to untangle the toughest problems in maths.

In Class 12, there are chapters all about integration. In one chapter called 'Integrals,' they teach different ways to solve integration. That's where they introduce substitution as a special trick. Later on, in another chapter called 'Application of Integrals,' they show how we can use integration in real life; about things like finding areas and volumes, but the cool part is using substitution to make the maths easier.

Integration isn't just for school; it's super useful in lots of places: In exams, knowing integration helps solve problems and get better grades. In college or jobs related to science and maths, understanding integration helps with more advanced stuff. In different careers like engineering or physics, knowing how to use integration in maths is really important. Even in daily life, it's like a secret maths tool that helps in measurements, finance, and understanding data better. This article discusses integration. It talks about different types of integration, cool tricks, and tips to simplify those integration problems. So keep reading, because this is where maths becomes super interesting and useful.

What is Integration?

Integration is like figuring out how much space there is under a wavy line on a graph. Imagine this line on a graph paper; integration helps find the area enclosed by that line. We do this by using small rectangles to cover the area under the line. We add up the sizes of all these rectangles to get close to the actual area under the line. It's like estimating the space by using lots of tiny pieces until we're really close to the real answer.

When we keep adding these tiny areas, we get closer and closer to the actual space under the line. It's like zooming in on the line bit by bit until we understand how much space it takes up.

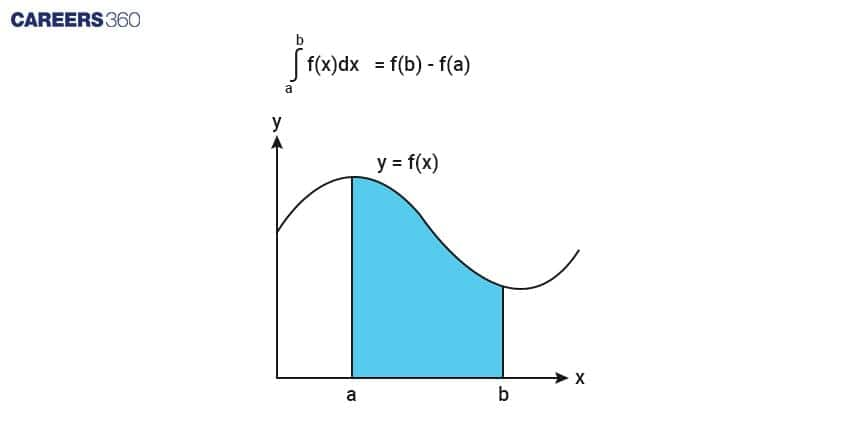
Integration is the reverse process of Differentiation

Integration is like the reverse of differentiation. When we're handed a derivative of a function and asked to discover its original form, that's where integration steps in. This process, known as anti-differentiation or integration, involves finding the primitive function—the original function from which the derivative was derived. It's like retracing our steps backward to reveal the starting point.

Let's say we have a function like f(x) = sin x. If we find its derivative, f'(x) = cos x, we're essentially working out the change rate of the original function. Here, cos x becomes the derived function of sin x. It's like saying cos x shows us how fast sin x is changing.

Types of Integration

>> Indefinite Integral: This type represents the general antiderivative of a function. It doesn't have specific limits, so it includes a constant of integration (usually denoted as "+ C"). It's like finding a family of functions that could be derived to get the original function.

>> Definite Integral: Unlike the indefinite integral, this type has specific limits. It calculates the exact area between the function and the x-axis within those limits. It gives a precise numeric value, representing the net area under the curve.

>> Improper Integral: These integrals involve infinite limits or functions that aren't bounded within a finite interval. Solving such integrals involves handling limits approaching infinity or negative infinity, and they require special techniques to find their values.

>> Line Integral: This type involves integrating a function along a curve or a path in a multi-dimensional space. It's used in fields like physics and engineering to calculate work done, circulation, or flux along a path.

>> Surface Integral: This integral type deals with integrating functions over a surface in a three-dimensional space. It's useful in physics, especially in calculating flux and flow through surfaces.

>> Volume Integral: Also known as a triple integral, this type deals with integrating functions over a volume in a three-dimensional space. It's frequently used in physics and engineering to calculate volumes of irregular shapes or densities.

>> Double Integral: This integral type is used for integrating functions over a two-dimensional region in a plane. It's often applied in calculating areas, centroids, and moments of 2D shapes.

>> Triple Integral: Similar to the double integral but in three dimensions, this type is used for integrating functions over a three-dimensional region. It's handy for calculating volumes, masses, and centroids of 3D objects.

Also Read | Crucial Concepts For Exams: Understanding Pipes And Cisterns

Method Of Integration

In certain cases, just looking at a function isn't sufficient to find its integral. Some functions pose a challenge and require additional methods to transform them into a standard form for integration. Several essential methods such as the decomposition method, integration using partial fractions, Integration by Parts, and integration by substitution. This article will discuss integration by substitution comprehensively.

>> Standard Substitution: Often used when the integral involves a function and its derivative. For instance, if you have ∫f(g(t))g'(t)dt in the integral, substituting x = g(t) can simplify it by converting everything into terms of x.

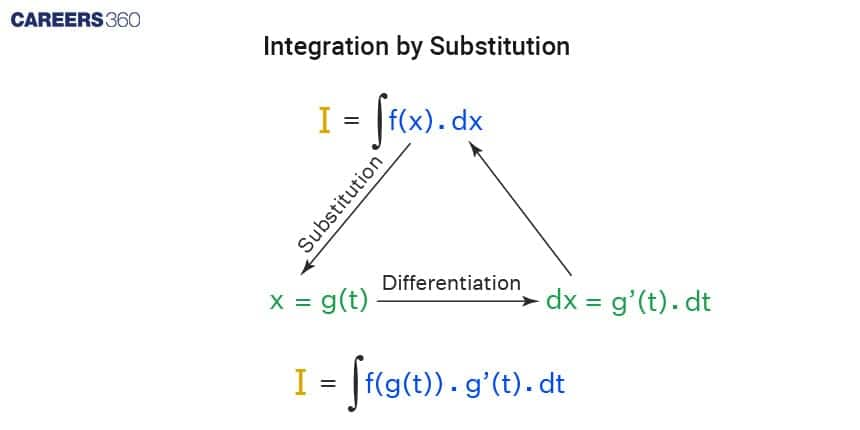
Consider the integral: ∫2x√(1 + x²) dx.

To solve this using standard substitution, we'll use u = 1 + x² as our substitution.

Let u = 1 + x².

du/dx = d/dx (1 + x²).

du/dx = 2x.

dx = du / (2x).

∫2x √(1 + x²) dx = ∫2x √(u)*(du / (2x)).

∫√(u) du = (2/3) * u^(3/2) + C, where C is the constant of integration.

(2/3) * u^(3/2) + C = (2/3) * (1 + x²)^(3/2) + C.

>> Binomial Substitution: Used when integrals contain expressions in the form of(a² - x²)ⁿ or (x² - a²)ⁿ. Substituting x = a sin(t) or x = a cos(t) is often employed in these cases.

>> Trigonometric Substitution: Useful for integrals containing radicals or expressions involving squares of trigonometric functions.

Consider the integral: ∫ √(4 - x²) dx

Let x = 2 sin(θ)

Then dx = 2 cos(θ) dθ

Now, we need to express the given integral in terms of θ:

∫ √(4 - x²) dx = ∫ √(4 - (2sin(θ))²) * 2cos(θ) dθ

Using the trigonometric identity: 1 - sin²(θ) = cos²(θ)

= ∫ √{4 - 4sin²(θ)}*2cos(θ) dθ

= ∫ √{4cos²(θ)} * 2cos(θ) dθ

= ∫ {2cos(θ)} * 2cos(θ) dθ

= ∫ 4cos²(θ) dθ

4cos²(θ) = 2(2cos²(θ)) = 2(1 + cos(2θ))

∫ 4cos²(θ) dθ = ∫ 2(1 + cos(2θ)) dθ

= 2∫ (1 + cos(2θ)) dθ

= 2(θ + (1/2)sin(2θ)) + C, where C is the constant of integration.

Now, we need to revert to the original variable x. Recall that x = 2 sin(θ). From this, we can derive θ = arcsin(x/2).

2(θ + (1/2)sin(2θ)) + C = 2(arcsin(x/2) + (1/2)sin(2arcsin(x/2))) + C

So, the final solution to the integral ∫ √(4 - x²) dx using trigonometric substitution is 2(arcsin(x/2) + (1/2)sin(2arcsin(x/2))) + C, where C is the constant of integration.

>> Secant Tangent Substitution: Helpful for integrals involving expressions of the form(x² - a²)ⁿ. Substituting x = a sec(t) or x = a tan(t) can simplify such integrals.

>> Exponential Substitution: Helpful for integrals involving exponentials or roots. For instance, substituting x = etcan simplify some exponential integrals.

Consider the integral: ∫x * e^{(x^2)} dx

Let's set u = x²

Then, du/dx = 2x

dx = du / (2x)

Now, substitute u = x² and dx = du / (2x) into the integral

∫x * e^{(x^2)} dx = ∫x * e^u * (du / (2x))

∫e^u * (du / 2)

= (1/2) ∫e^u du

= (1/2) * e^u + C, where C is the constant of integration.

= (1/2) * e^{(x^2)} + C

>> Inverse Function Substitution: Useful for integrals involving inverse trigonometric functions (arcsin, arccos, arctan). Substitutions involving these inverse functions can simplify such integrals.

Also Read| What Are Exponential And Logarithmic Functions, And How Do They Work?

Hope this helps you to understand the concept of integration, types of integration, different methods, specifically substitution method of integration and how these concepts can be applied in real life issues.