How Can Algebra And Vectors Bring Imagination To Life?

Animation is an incredible art form that makes images come to life on your screen. It may be fun to watch, but did you have an inkling that it is also a great way to learn maths and science? In this article, we'll explore how algebra and vectors, two essential mathematical tools, work in animation.

These Maths concepts are primarily discussed in the Class 12 NCERT curriculum. We'll also look at how understanding these concepts can help students score well in board exams and competitive exams, such as JEE (Joint Entrance Examination).

The Wonders Of Animation

Think of your favourite animated movie or TV show. It's filled with characters that move and interact. How do animators make all of this happen? Well, that's where algebra and vectors come into play. But let's start with the basics.

Animation: A Quick Overview

Imagine a world where pictures come alive, where characters move and things happen. This magical world is called animation. But how does it work?

In animation, we make things look like they're moving by showing a lot of pictures really fast. These pictures are called frames. Even though they're just separate pictures, when we show them quickly, they create the feeling of motion. It's a bit like flipping through a book so fast that the pictures seem to come to life.

Also Read |Derivatives And Economics: How They Help Analyse Market Trends?

Mathematical Equations In Animation

These equations enable animators to transform imagination into mesmerising on-screen motion pictures.

Linear Interpolation (LERP): Creating Smooth Transitions

Linear interpolation, often abbreviated as LERP, is a fundamental mathematical concept that forms the basis for creating smooth transitions and movements in animations. Like the magician's wand, LERP allows animators to interpolate or transition between two values, making animations appear fluid and continuous.

Linear interpolation between two given points can be visualised geometrically as follows:

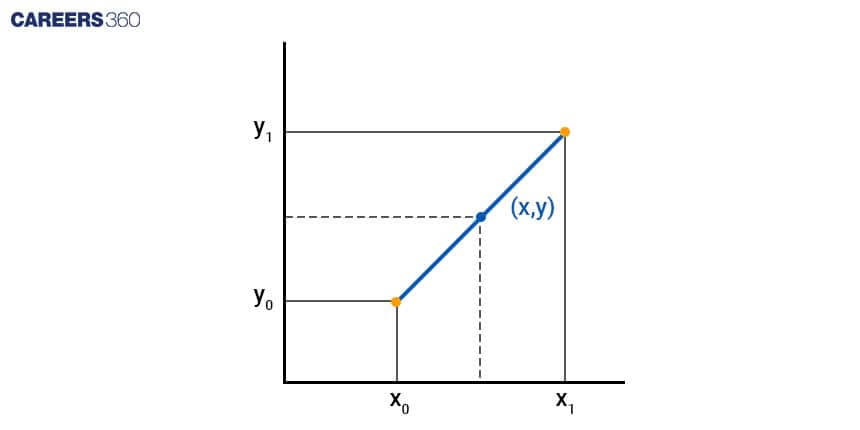
The value at a point represented by the green circle, when multiplied by the horizontal distance between the points marked by the red and blue circles, equals the sum of the value at the red circle, multiplied by the horizontal distance between the green and blue circles, and the value at the blue circle, multiplied by the horizontal distance between the green and red circles.

If the coordinates of the two known points are given as (x₀, y₀) and (x₁, y₁), the linear interpolant represents the straight line that connects these two points. For a value x in the interval (x₀, x₁), the corresponding y value along the straight line can be determined using the equation of slopes:

(y - y₀) / (x - x₀) = (y₁ - y₀) / (x₁ - x₀).

This equation can be derived geometrically based on the associated figure. It's a specific case of polynomial interpolation when n = 1. Solving this equation for y, the unknown value at x, results in:

y = y₀ + (x - x₀) * (y₁ - y₀) / (x₁ - x₀),

which is the formula for linear interpolation within the interval (x₀, x₁). Beyond this interval, the formula remains identical to linear extrapolation.

LERP is widely used for creating movements such as character animations, camera pans, and scene transitions. It ensures that animations appear seamless and natural.

Vector Equations: Guiding Motion and Direction

Vectors are the guiding stars of animation. They are mathematical entities that provide both direction and magnitude, making them essential tools for describing motion and positioning objects. In animation, various vector equations are used to control character movements, camera positions, and object trajectories.

Example: Vector Addition

Imagine you have two vectors A(x₁, y₁) and B(x₂, y₂). To find their addition, you simply add their corresponding components:

C(x₁ + x₂, y₁ + y₂)

These vector equations are the building blocks for animating characters, guiding camera movements, and creating realistic motions.

Also Read | Cancer Treatment: Why Chemotherapy Does Not Suit All Patients?

Quadratic Equations: Defining Curves and Paths

Quadratic equations are employed to define curves and paths in animations. These equations are fundamental for creating natural and realistic trajectories. They help in shaping the motion of characters, objects, and particles, giving life to animation sequences.

Mathematical Equation:

The general form of a quadratic equation is: ax² + bx + c = 0

Where 'a', 'b', and 'c' are constants that define the shape and position of the curve. By altering these constants, animators can craft a wide range of curves, from parabolic jumps to elegant arcs.

Trigonometric Functions: Adding Realism to Rotations

Trigonometry comes into play when animators need to create rotations and oscillations. Sine and cosine functions are the heroes of smooth and periodic motion in animation.

Mathematical Equation (Sine Wave): y(t) = A * sin(ωt + φ)

In this equation, 'A' represents the amplitude, 'ω' is the angular frequency, 't' is time, and 'φ' is the phase. Sine and cosine functions are employed for animating swinging pendulums, rotating wheels, and all sorts of periodic motions in animation.

Easing Equations: Adding Realistic Acceleration

Easing equations are the tools that control acceleration and deceleration in animations, making movements look natural and visually appealing. These equations determine how quickly an object should start, stop, or change its speed during an animation.

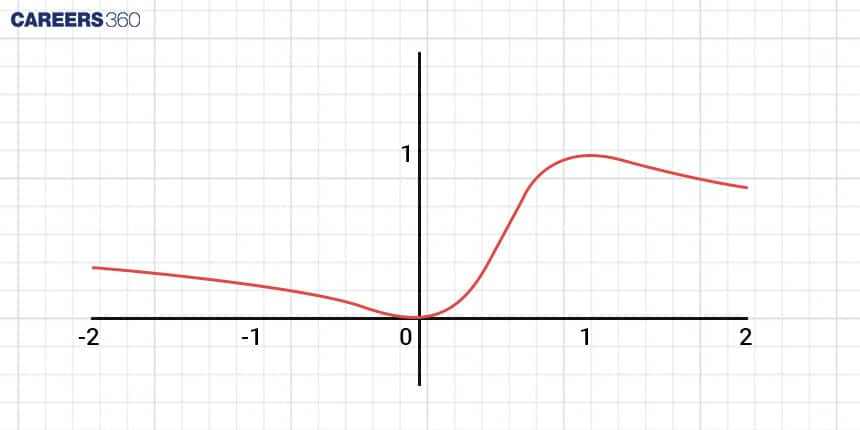
Mathematical Equation (Ease In-Out): f(t) = t² / (t² + (1 - t)²)

Easing equations are essential for creating animations that don't appear mechanical but instead mimic the way objects move in the real world. They make animations feel more natural and pleasing to the eye.

Also Read | Condensation: What Is Science Behind Droplets Forming On Chilled Surface?

Matrix Transformations: Performing Complex Operations

Matrices are the magic spells in the animator's toolkit. They enable animators to perform multiple transformations simultaneously, saving time and ensuring smooth animations.

Mathematical Equation (3D Transformation): Scaling + Rotation + Transition

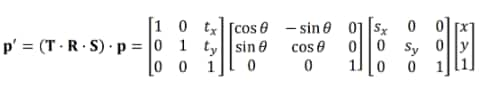
This equation represents a 3D transformation matrix, which combines scaling (resizing), rotation (turning), translation (moving) and into one operation. Matrices are invaluable when animating complex movements, such as those involving characters, objects, or camera angles.

Kinematics Equations: Bringing Characters to Life

Kinematics equations are the backbone of character animation, providing the means to calculate positions, velocities, and accelerations based on time and motion parameters. These equations ensure that animated characters move realistically, with accurate and consistent motion.

Example: Position Equation for Constant Acceleration

x(t) = x₀ + v₀ * t + 0.5 * a * t²

In this equation, 'x(t)' represents the position of the character at time 't,' 'x₀' is the initial position, 'v₀' is the initial velocity, 'a' is the acceleration, and 't' is the time. Kinematics equations are vital for animating characters' walks, runs, and jumps, making their movements appear lifelike.

Animation and Exams

Understanding animation with maths is not just fun; it's also a great way to improve your exam scores. Whether it's your board exams or competitive exams like JEE, having a strong foundation in maths and knowing how to apply it can make a big difference.

Boosting Scores in Board Exams

In your board exams, having a good grasp of maths is essential. You'll often encounter questions that test your mathematical skills and problem-solving abilities. Understanding how algebra, vectors, and matrices work in animation can give you an advantage. It sharpens your mathematical thinking, and you'll find solving maths problems in your exams much more manageable.

Improving Competitive Exam Performance

If you're preparing for competitive exams like JEE, you'll know that maths plays a crucial role. JEE exams are known for their tough maths questions. By understanding the practical application of maths in animation, you'll be better equipped to tackle complex problems.