How Does Maths Make Sports Better For Players?

In the world of modern sports, getting the best out of a team is not just about skills and hard work. Maths, particularly calculus, has become a game-changer in sports analysis. In this article, we'll see how using maths can help teams perform better in various sports, from baseball to basketball, using everyday language.

Calculus helps us understand and improve athletic performance, prevent injuries, and create smarter game plans. It's not just about complicated maths—it's about how maths can make athletes and teams better. We'll explore the basic maths ideas, formulas, and strategies that make it all possible. Whether it's predicting where a baseball will go or making quick decisions on the field, calculus is the secret weapon in sports analytics that can help teams shine.

Basics Of Calculus In Sports Analytics

Let's break down the fundamental ideas of calculus, making them easy to grasp for everyone, especially in the context of sports.

Derivatives: The Speed of Change

Imagine you're tracking a runner in a race, and you want to know how fast they're going at any given moment. Derivatives help with that. Here's how:

>> Speed and Velocity

• Speed means how quickly something is moving. To figure out how fast a runner is, you look at how their position changes in tiny moments. That's where derivatives come in.

For example, if a runner travels five metres in just one second, their speed is five metres per second (5 m/s). You find this by dividing the distance travelled by the time taken.

So, Speed (v) = Distance (Δx) / Time (Δt).

Here, v = 5 m/s.

>> Acceleration

• Acceleration is like speed's cousin. It shows how fast something is speeding up or slowing down. In sports, it's super useful to understand quick bursts of speed or sudden stops.

For example, think of a car. If it goes from zero to 60 miles per hour in 10 seconds, the acceleration is six miles per hour per second (6 mph/s). You calculate it by looking at how the speed changes in a given time.

Acceleration (a) = Change in velocity (Δv) / Time (Δt).

Integrals: Adding Things Up

Integrals help us tally up all the small stuff to get the big picture. In sports, this is like adding up all the bits of data to understand how well a player or team is doing over time. Here are the key points:

>> Total Distance Covered

• Integrals are like a super calculator that can add up all the tiny distances a player moves in short bits of time to tell you how far they've gone.

For example, imagine a player in a basketball game. They move two metres in the first second, three metres in the next, and so on. To find out how far they've travelled in 10 seconds, you use an integral. It's like adding up all those little steps they took.

>> Averages

• Integrals are great for finding averages. In sports, this helps you understand how well a player performs on average during a game or over a season.

Picture a runner in a marathon. To know their average speed for the whole race, you use an integral. It calculates the overall average speed by adding up all their different speeds throughout the race.

These basic calculus ideas are like having secret tools in sports. They let you see the game in detail, whether tracking players, figuring out speed and acceleration, or understanding the total distances covered. Now, we'll see how these tools work in real sports situations to make teams perform better.

Trajectory Analysis

In sports such as baseball or golf, the analysis of projectile motion is essential. The trajectory of a projectile can be described using the following equations of motion:

Position Equation

x(t) = x₀ + v_0xt

y(t) = y₀ + v_0yt - (1/2)gt²

Velocity Equation

v_x(t) = v_0x

v_y(t) = v_oy - gt

Where: x and y represent horizontal and vertical positions, v_x and v_y are horizontal and vertical velocities, x₀ and y₀ are initial positions, v_0x and v_0y are initial velocities, g is the acceleration due to gravity, t is time.

These equations allow us to predict the path of a baseball, accounting for factors like initial speed, angle, and air resistance.

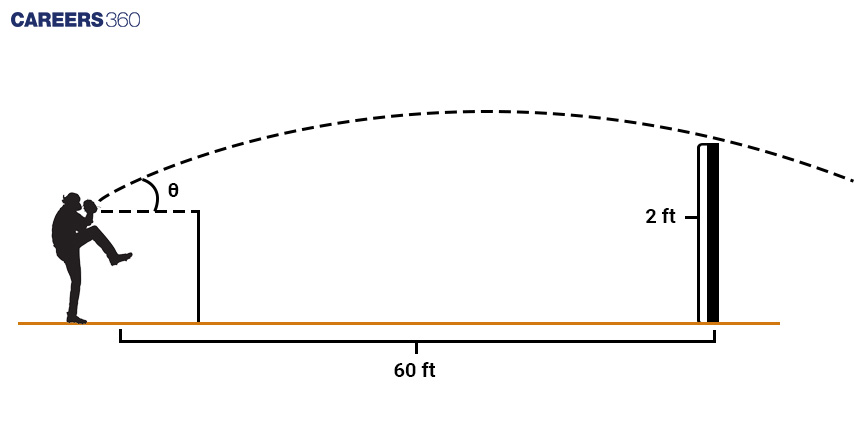
Let’s consider an example. A pitcher wants to throw a curveball that crosses the plate 60 feet away from the pitching mound, at a height of two feet, and at a speed of 90 miles per hour. The pitcher needs to determine the launch angle (θ) for the curveball.

We can use the equations of motion to model the trajectory of the curveball.

Horizontal motion: x(t) = x₀ + v₀cos(θ)t

Vertical motion: y(t) = y₀ + v₀sin(θ)t - (1/2)gt²

y(t) = x(t)tan(θ) - (1/2)g{x(t)²/(v₀²)}sec²(θ)

We want the curveball to cross the plate at a horizontal distance of 60 feet and a height of two feet. Therefore, at that point, we have x = 60 feet and y = 2 feet.

We are also given the speed v0 in miles per hour, but we need to convert it to feet per second.

Convert the speed to feet per second:

v₀ = 90 mph * (5280/3600) ft/s

≈ 132 ft/s

Plug in the values for x and y:

2 = 60 tan(θ) - 16(60²/ 132²).sec²(θ)

2 = 60 tan(θ) - 3.305785 (1 + tan²θ)

3.305785 tan²θ - 60 tan(θ) + 5.305785 = 0

After solving the quadratic equation we get.

tan(θ) = 18.0611

tan(θ) = 0.0888648

Player Movement Analysis

Player tracking systems, like GPS or video analysis, provide position data over time. Calculus helps analyse this data. By finding the derivative of position with respect to time, one obtains velocity, and further differentiation yields acceleration:

Velocity: v(t) = dx(t)/dt

Acceleration: a(t) = dv(t)/dt

These concepts are crucial for understanding a player's performance and can be used to optimise strategies and training.

Performance Optimisation

Calculus is essential for optimising training regimens. We can use differential equations to model how an athlete's physical attributes change with training over time and find the optimal training regimen:

dP(t)/dt = k * F(t)

Here, P(t) represents performance (e.g., speed) at time t, F(t) represents the effect of training at time t, and k is a constant representing the rate at which performance improves.

Injury Prevention

Biomechanics and calculus are used to analyse forces on an athlete's body. For instance, when an athlete runs, the ground reaction force can be modelled using differential equations, allowing us to assess the impact on joints and muscles for injury prevention.

Game Strategy and Probability

Calculus can be applied to model the probability of events during a game. For instance, in basketball, the probability of a successful shot can be represented as a function of distance and angle from the hoop:

P(success) = f(distance, angle)

Calculus helps us find the optimal shooting positions and angles to maximise the probability of success.

Simulation and Modeling

Calculus underpins mathematical models that simulate game scenarios. For example, differential equations can describe player fatigue overtime during a game, taking into account factors like work rate and recovery. Simulations provide insights into optimal strategies under changing conditions.

Hope that now you have a clear and complete grasp of how maths plays a vital role in sports, from analysing performance to optimising teams.