Breaking Down Einstein's Theory Of Relativity And Mathematics
Albert Einstein's Theory of Relativity formulated over a century ago, has far-reaching implications and has been instrumental in shaping modern physics. Interestingly, mathematics plays a crucial role in Einstein's Theory of Relativity, and understanding the mathematical concepts behind it can significantly enhance your preparation for competitive exams such as JEE (Joint Entrance Examination), NEET (National Eligibility cum Entrance Test), and board exams. In this article, we will explore the relevance of Einstein's Theory of Relativity to these exams, and the underlying mathematics, and provide solved problems that align with the competitive exam syllabus.

Relevance To Competitive Exams
Competitive exams such as JEE, NEET, and Board exams test students' comprehensive understanding of scientific concepts and their problem-solving skills. Einstein's Theory of Relativity is an important topic in physics that is often included in the syllabi of these exams. Familiarity with the theory and its mathematical foundations can help students tackle related questions with confidence and precision. Moreover, demonstrating knowledge of this theory showcases a deeper understanding of physics, which can set students apart from their peers during the exam evaluation process.
In the NCERT curriculum, the chapter Gravitation in the Class 11 Physics textbook provides an introduction to the concepts related to Einstein's Theory of Relativity. While this chapter primarily focuses on Newtonian gravity and its applications, it also mentions the need for a new theory to explain phenomena at high speeds and in extreme gravitational fields. It briefly alludes to the principles of Special and General Relativity, emphasising their significance in understanding the fundamental nature of the universe.
Mathematics Behind Einstein's Theory Of Relativity
Einstein's Theory of Relativity involves several mathematical concepts that underpin its formulation and predictions. Here are some key mathematical ideas associated with the theory:
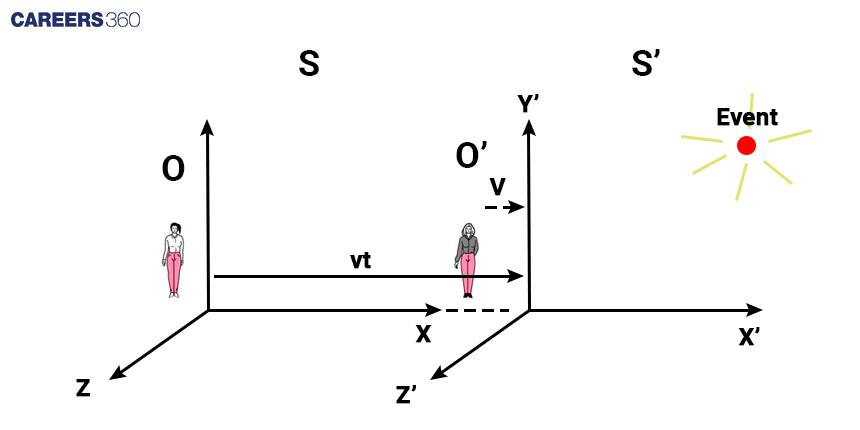
Lorentz Transformation
The Lorentz transformation is a mathematical equation that describes how space and time coordinates change when transitioning between reference frames moving relative to each other. It is the basis of Special Relativity, which deals with objects moving at constant velocities in the absence of gravitational fields.
Consider two reference frames: the "primed" frame (denoted by the variables x', y', z', t') and the "unprimed" frame (denoted by the variables x, y, z, t). The primed frame moves with a constant velocity v relative to the unprimed frame along the x-axis.
Also Read | What Is The Role Of Statistics In Modern Physics: A Mathematical Perspective
The Lorentz transformation equations for the coordinate transformation are as follows:
x' = γ(x - vt)
y' = y
z' = z
t' = γ(t - vx/c2)
Here, γ (gamma) represents the Lorentz factor and is defined as
γ = 1 / √(1 - (v2 / c2))
Where v is the relative velocity between the frames and c is the speed of light.
Let's illustrate the application of the Lorentz transformation with an example:
Example: An observer in the unprimed frame measures an event as (x, y, z, t) = (4 m, 0 m, 0 m, 0 s). The primed frame moves with a velocity of 0.6c (where c is the speed of light) relative to the unprimed frame along the positive x-axis. Determine the event's coordinates (x', y', z', t') as observed in the primed frame.
Solution: To find the transformed coordinates, we need to apply the Lorentz transformation equations. First, we calculate the Lorentz factor γ:
γ = 1 / √(1 - (v2 / c2))
= 1 / √(1 - (0.6c)2 / c2)
= 1 / √(1 - 0.36)
≈ 1.25
Now, we can substitute the values into the transformation equations:
x' = γ(x - vt)
= 1.25(4 m - 0.6c * 0 s)
= 1.25(4 m)
= 5 m
y' = y = 0 m
z' = z = 0 m
t' = γ(t - vx/c2)
= 1.25(0 s - 0.6c * 4 m / c2)
= 1.25(-2.4 s)
≈ -3 s
Therefore, the event's coordinates in the primed frame are (x', y', z', t') = (5 m, 0 m, 0 m, -3 s).
Spacetime Geometry
In General Relativity, Einstein introduced the concept of spacetime, a four-dimensional continuum that combines space and time. The mathematical framework of General Relativity involves the use of tensor calculus to describe the curvature of spacetime caused by matter and energy.
Equivalence Principle
The Equivalence Principle is a foundational principle in General Relativity, stating that the effects of gravity are indistinguishable from the effects of acceleration. This principle allows the formulation of a new theory of gravity, where the gravitational force arises due to the curvature of spacetime.
Also Read | 5 Must Watch Documentaries On Fascinating Truths Of Biology
Field Equations
The field equations of General Relativity, known as Einstein's equations, are a set of ten coupled, nonlinear partial differential equations. These equations relate the curvature of spacetime to the distribution of matter and energy within it.
The field equations can be written as:
Rμν - (1/2)Rgμν = 8πGTμν
Where,
Rμν = Components of the Riemann curvature tensor
R = Scalar curvature
gμν = Metric tensor
Tμν = Energy-momentum tensor
G = Gravitational constant
c = Speed of light.
Solved Problems
To help you apply the concepts of Einstein's Theory of Relativity to competitive exams, here are some solved problems that align with the syllabus and test your understanding:
Problem: Consider a massive object with a density of 1.5 × 10^3 kg/m^3. Calculate the radius at which the object's escape velocity equals the speed of light (c).
Solution:
According to General Relativity, the escape velocity from a massive object is given by
Ve = √(2GM/r)
Where G is the gravitational constant, M is the mass, and r is the radius.
To find the radius at which the escape velocity equals the speed of light.
Ve = c
Substituting the given values, we have
c = √(2GM/r)
Solving for r, we get r = 2GM / c2
Substituting the appropriate values and calculating yields the radius r ≈ 4.44 × 10^3 metres.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
