Why Do Roads Have Curves? How Differentiation Ensures Safety

As civilisation advances, the need for efficient and safe transportation becomes increasingly important. Highways play a crucial role in connecting people and goods across regions, and their design requires precision and thoughtful planning. Interestingly, mathematics, specifically differentiation, lies at the heart of highway design. In this article, we will explore the application of differentiation in highway design, focusing on curvature and safety aspects of roads. This article is aimed at Class 11 and Class 12 students, explaining the types of roads in terms of curves, slopes, and many more, and how a solid understanding of mathematical concepts can lead to success in academics and competitive exams like NEET, JEE, CBSE, and Board exams.

Role Of Differentiation In Highway Design

Differentiation, a fundamental concept in calculus, is the mathematical tool used to understand the rate of change of a function. In highway design, engineers employ differentiation to calculate and analyse the slopes, curvatures, and gradients of the roads. These crucial design elements ensure smooth traffic flow, minimise accidents, and enhance overall road user safety. By utilising differentiation, engineers can optimise road design to create efficient, cost-effective, and safe transportation systems.

Types Of Roads Based On Curvature And Slope

Curved Roads

Curved roads are designed with horizontal curves, allowing them to follow the natural terrain and navigate through hilly or mountainous regions. The curvature of a road is vital in ensuring safe driving conditions, especially when vehicles need to make turns while maintaining a reasonable speed. Differentiation plays a central role in calculating the radius of curvature, which defines the sharpness of a curve.

Radius Of Curvature

Let's consider a curve represented by the function y = f(x). The radius of curvature at any point (x, y) on the curve:

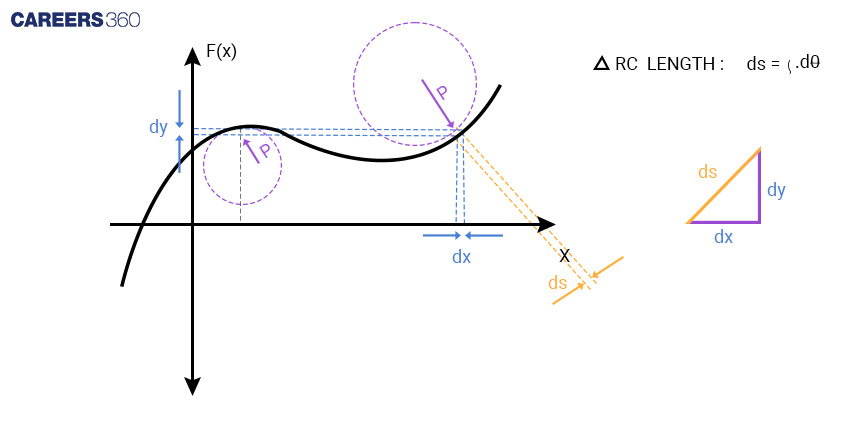
ds = ρdθ .........................(1)

In right angle triangle

ds = √{dx² + dy²}

ds = √{1+(dy/dx)²}dx..........(2)

We know

tanθ = dy/dx = d(tanθ)/dx

= d(dy/dx)/dx = d²y/dx²

(1 + tan²θ)dθ/dx = d²y/dx²

dθ = [d²y/dx²/(1 + tan²θ)]dx

dθ = [(d²y/dx²)/{1+(dy/dx)^2}]dx………(3)

Using equation (1), (2), and (3)

√{1+(dy/dx)²}dx = ρ.[(d²y/dx²)/{1+(dy/dx)²}]dx

ρ = [{1+(dy/dx)²}^3/2]/(d²y/dx²)

Where dy/dx represents the first derivative of y with respect to x, and d²y/dx² represents the second derivative of y with respect to x.

Turning On Horizontal Road

Let's consider a car of mass m running on a curved path shown below.

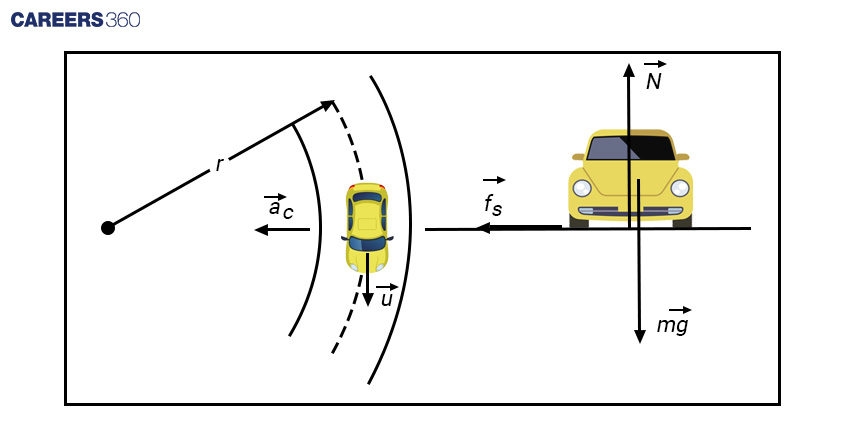
We know that in a circular motion,

Centripetal force = F = mV²/r

The friction between tire and road act as a centripetal force

Centripetal force = f = mV²/r

μN = μmg = mV²/r, where friction f = μN = μmg

r = V²/μg

This means form speed limit V and friction coefficient the radius of curvature can be r = V²/μg

V_max = √(μrg)

Banking Without Friction

The concept of road banking involves tilting the surface of curved roads to ensure a safe turning experience. When a car of mass 'm' travels at speed 'v' along a curved road with a radius of curvature 'R,' and the road is inclined at an angle 'θ' to the horizontal, the horizontal component of the normal force serves as the centripetal force required for the turn.

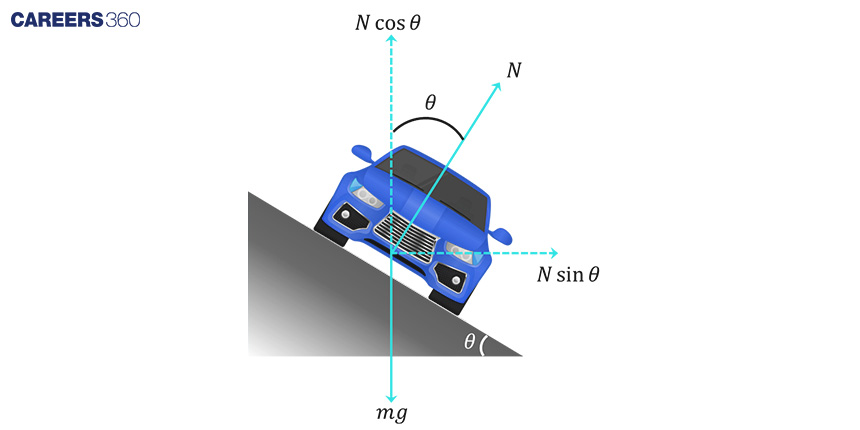
The component N balances the weight of the car and component N provides the centripetal force.

Therefore, in a circular motion,

N cosθ = mg

N sinθ = mV²/r

tan θ = v²/rg
V_max = √(rg tanθ)

Superelevation

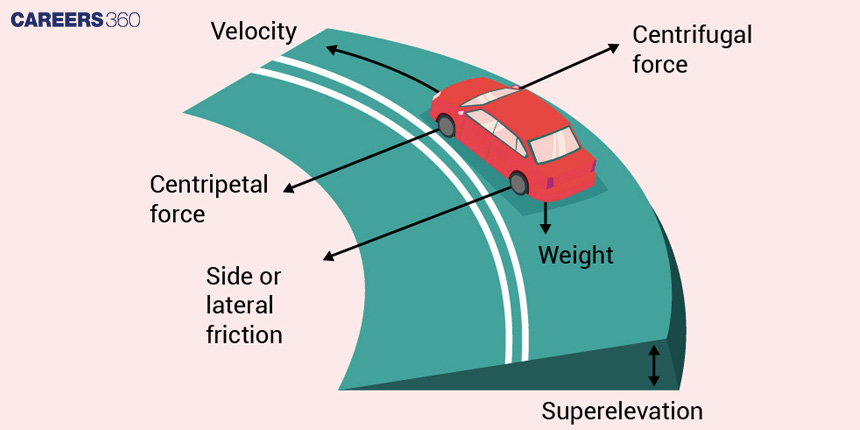
Superelevation, also known as banking, refers to the intentional tilting or banking of a roadway at an angle when a vehicle approaches a curve. This engineering technique makes it easier for motorists to navigate the curve at a safe speed without skidding or tipping over. By implementing superelevation, drivers can maintain both safety and optimal speeds on curved roads. Without this design feature, vehicles would be more prone to sliding, skidding, or even tipping and rolling over, especially in wet or icy conditions or when travelling at high speeds. Superelevation enables traffic to maintain a certain speed through curves, preventing excessive slowdowns each time the road bends.

Let's understand this concept mathematically.

In this case, the direction of friction depends on the speed of the car. Imagine a car with mass (m) travelling at speed (v) along a curved road with a radius of curvature (R) and a banking angle (θ) The friction force acting along the radial direction is a self-adjusting force that varies according to the car's velocity to prevent slipping.

Case 1: Calculation of Maximum speed limit (V_max)

The car's velocity, at the point of reaching the maximum friction limit, represents the highest speed it can attain without slipping. At this juncture, friction acts downward along the surface of the banked road since the car tends to slip upward.

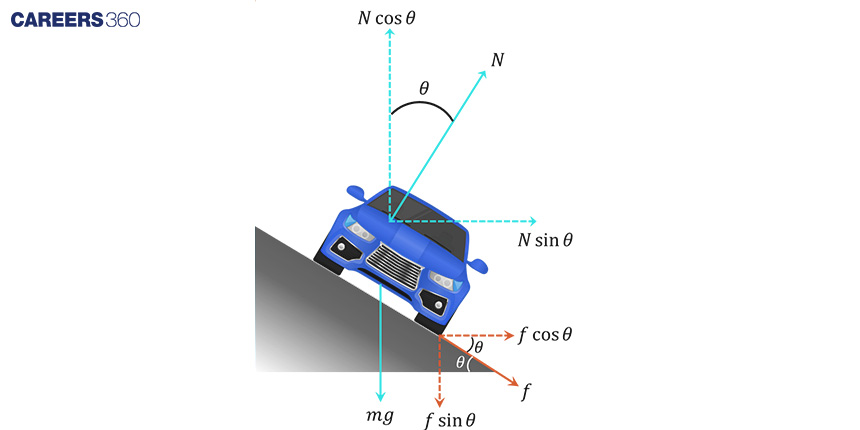
Friction can be calculated as f = μN

Balancing the force

N cosθ = mg + f sinθ

N cosθ - μN sinθ = mg.......(1)

N sinθ + f cosθ = mV²/R

N sinθ + μNcosθ = mV²R.........(2)

Using equations (1) and (2)

(cosθ -μsinθ)/(sin θ + μ cosθ) = gR/V²

V_max = √[gR{(μ+ tanθ)/(1-μtan θ)}]

Case2: Calculation of Minimum speed limit (V_min)

In this scenario, friction acts upward along the plane of the banked road because the car tends to slide downward.

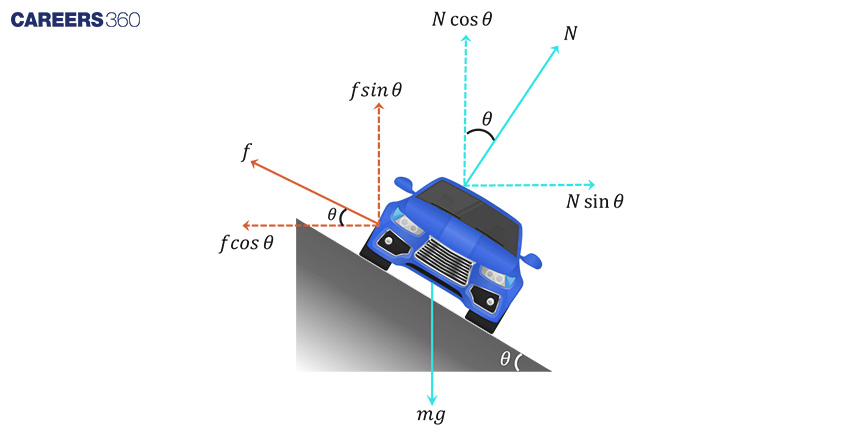
Friction can be calculated as f = μN

Balancing the force

N cosθ + f sinθ = mg

N cosθ + μN sinθ = mg.......(1)

N sinθ - f cosθ = mV²/R

N sinθ - μNcosθ = mV²R.........(2)

Using equations (1) and (2)

(cosθ + μsinθ)/(sin θ - μ cosθ) = gR/V²

V_max = √[gR{(μ - tanθ)/(1 + μtan θ)}]

Safe speed is given as

√[gR{(μ+ tanθ)/(1-μtan θ)}] < Speed < √[gR{(μ - tanθ)/(1 + μtan θ)}]

Relevance For Students

A thorough understanding of the mathematical concepts involved in designing curved and sloped roads can significantly benefit students in various ways:

Academic Performance: Studying the applications of differentiation in highway design provides students with a practical perspective on how mathematical concepts are used in real-world scenarios. This understanding can lead to improved performance in mathematics and related subjects.

Problem-Solving Skills: By solving mathematical problems related to road curvature and slope, students can enhance their analytical and problem-solving skills. These skills are valuable not only in academic settings but also in various professions.

Competitive Exams: Knowledge of differentiation and its applications in highway design is relevant to competitive exams such as NEET, JEE, CBSE, and Board exams. These exams often include questions that require applying calculus concepts to solve real-world problems.

Engineering and Career Opportunities: For students aspiring to pursue careers in civil engineering or related fields, a solid grasp of differentiation and its application in highway design is essential. This knowledge forms the foundation for advanced courses and research in civil engineering.