RD Sharma Class 12 Exercise 2.1 Function Solutions Maths

RD Sharma Class 12 Exercise 2.1 Function Solutions Maths - Download PDF Free Online

Edited By Team Careers360 | Updated on Jan 20, 2022 10:35 AM IST

Students in class 12 will have to concentrate on their studies and prepare well in advance for their upcoming boards. RD Sharma class 12th exercise 2.1 will be of great help to students. With RD Sharma class 12th mathematics solutions, you will get the best answers all in one place. RD Sharma Solution It will provide you with a clear understanding of all the concepts to ace your mathematics paper.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics

RD Sharma Class 12 Solutions Chapter 2 Functions - Other Exercise

Functions Excercise:2.1

Functions exercise 2.1 question1(i)

$f(x)=2x$
Given:
The example for a function which is one-one but not onto.
Hint:
One-one function means every element in the domain has a distinct image in the co-domain
. $f(x_1)=f(x_2)$ , then $x_1=x_2$
Where, $X_1,X_2$ domain of $f(x)$
Onto function defined as every element in the co-domain has at least one pre image in the domain of function.
Solution:
Here, we need to give an example of a function for one-one but not onto.
Let we consider the function,
$f:N \rightarrow N$ , given by $f(x)=2N$
Let us consider two elements $x_1$ and $x_2$ in the domain of f, so we get
$f(x_1)=2x_1$ and $f(x_2)=x_2$
Now we know the condition for finding a one-one function.
$2x_1= 2x_2$
$x_1= x_2$
Hence, the function is one-one.
Now, we need to prove $f(x)=2x$ is not onto
Let $f(x)=y$ , such that x, $y\in N$
We get,
$2x=y$
$x=\frac{y}{2}$
If we put $y=1,$
$x=\frac{1}{2}=0.5$ , which is cannot be true as $x \in N$ supposed in solution.
Hence, the given function is not onto.
So, $f(x)=2x$ is an example of one-one but not onto function.

Functions exercise 2.1 question 1 (ii)

$f(x)=y$
Given:
The example for a function which is not one-one but onto.
Hint:
One-one function means every element in the domain has a distinct image in the co-domain. If one-one is given for any function. $f(x_1)=f(x_2)$ , then $x_1=x_2$
Where, $x_1,x_2 \in$ domain of $f(x)$
Onto function defined as every element in the co-domain has at least one pre image in the domain of function.
Solution:
Here, we need to give an example of a function for a not one-one but onto function.
Let the function $f:N \rightarrow N$ , given by $f(1)=f(2)=1$
Here, $f(x)=f(2)=1$
$f(x)=f(1)=1$
Since different elements $1,2$ have same image 1,
$\therefore f$ is not one-one.
Let $f(x)=y$ , such that $y\in N$
Here,y is a natural number and for every y there is a value of x which is a natural number.
Hence,f is onto.
So, the function $f:N \rightarrow N$ , given by $f(1)=f(2)=1$ is not one-one but onto.

Functions exercise 2.1 question 1 (iii)

The example for a function which is neither one-one nor onto.
Hint:
One-one function means every element in the domain has a distinct image in the co-domain. If one-one is given for any function $f(x)$ as if $f(x_1)=f(x_2)$ , then $x_1=x_2$
Where, $x_1,x_2\in$ domain of $f(x)$
Onto function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Let function $f:N \rightarrow N$ , given by $f(x)=x^2$
Calculate $f(x_1)$ and $f(x_2)$
$\begin{aligned} &f\left(x_{1}\right)=x_{1}^{2} \\ &f\left(x_{2}\right)=x_{2}^{2} \\ &\left(x_{1}\right)^{2}=\left(x_{2}\right)^{2} \\ &x_{1}=x_{2} \text { or } x_{1}=-x_{2} \end{aligned}$
Since, $x_1$ doesn’t have unique image,
Now,
$f(x)=x^2$
Let $f(x)=y$ such that $y\in R$
$x^2=y$
$x=\pm \sqrt{y}$
Since y is real number, then it can be negative also.
If $y=-2, x=\pm \sqrt{-2}$ which is not possible as the root of a negative number is not real.
Hence,x is not real, so f is not onto.
$\therefore$ Function $f:N \rightarrow N$ given by $f(x)=x^2$ is neither one-one nor onto.

Functions exercise 2.1 question 2 (i)

$f_1$ is one-one and onto function.
Given:
$f_{1}=\{(1,3),(2,5),(3,7)\} ; A=\{1,2,3\} ; B=\{3,5,7\}$
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the codomain has at least one pre image in the domain of function.
Solution:
We need to find the one-one function
Injectivity: (one-one)
$\begin{aligned} &f_{1}(1)=3 \\ &f_{1}(2)=5 \\ &f_{1}(3)=7 \end{aligned}$
Every element of A has different images in B.
$\therefore$ Function $f_1$ is one-one.
Surjectivity: (onto)
Co-domain of $f_1= \left \{ 3,5,7 \right \}$
Range of $f_1$ set of image $\left \{ 3,5,7 \right \}$
Co-domain=Range
So, $f_1$ is onto.

Functions exercise 2.1 question 2 (ii)

$f_2$ is one-one and onto function.
Given:
$f_{2}=\{(2, a),(3, b),(4, c)\} ; A=\{2,3,4\} ; B=\{a, b, c\}$
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the codomain has at least one pre image in the domain of function.
Solution:
We need to find the one-one function
Injectivity:
$\begin{aligned} &f_{2}(2)=a \\ &f_{2}(3)=b \\ &f_{2}(4)=c \end{aligned}$
Every element of A has different images in B.
$\therefore$ Function $f_2$ is one-one.
Surjectivity:
Co-domain of $f_2=\left \{ a,b,c \right \}$
Range of $f_2=$ set of image $\left \{ a,b,c \right \}$
Codomain = Range
So, $f_2$ is onto

Functions exercise 2.1 question 2 (iii)

$f_3$ is not one-one and onto function.
Given:
$f_{3}=\{(a, x),(b, x),(c, z),(d, z)\} ; A=\{a, b, c, d\} ; B=\{x, y, z\}$
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the codomain has at least one pre image in the domain of function.
Solution:
We need to find the one-one function
Injectivity: (one-one)
$\begin{aligned} &f_{3}(a)=x, f_{3}(c)=z \\ &f_{3}(b)=x, f_{3}(d)=z \end{aligned}$
Here $f_3(a),f_3(b)$ have the same image x
Also $f_3(c),f_3(d)$ have the same image z
Therefore, $f_3$ is not one-one.

Functions exercise 2.1 question 3

$f:N \rightarrow N$ , given by $f(x)=x^2+x+1$ is one-one but not onto.
Hint:
Let x and y be any two elements in the domain (N), such that $f(x)=f(y)$
So,f is one-one.
Given:
$f:N \rightarrow N$ , defined by $f(x)=x^2+x+1$
Let us prove that the given function is one-one.
Solution:
We have $f(x)=x^2+x+1$ … (i)
Calculate $f(y)=y^2+x+1$ … (ii)
Now equate equation (i) and (ii)
$\begin{aligned} &f(x)=f(y) \\ &x^{2}+x+1=y^{2}+y+1 \\ &x^{2}+x-y^{2}-y=0 \end{aligned}$
$\begin{array}{r} x^{2}-y^{2}+x-y=0 \\ {\left[\because a^{2}-b^{2}=(a+b)(a-b)\right]} \\ (x+y)(x-y)+x-y=0 \\ (x-y)[(x+y+1)]=0 \end{array}$
From (iii) equation, we can write
$x-y=0, x+y+1\neq 0$
$x+y+1\neq 0$ , because if we substitute $x=1, y= 1$
$1+1+1=3$
Hence, $x+y+1\neq 0$ for any $x\in N$
Where as,
$x-y =0$
$x=y$
So,f is a one-one function.
But, $f(x)=x^3+x+1\geq 3$ for all $x\in N$
So, $f(x)$ doesn’t assume values of1 and 2
$\therefore f$ is not an onto function.
Hence, we proved that, $f(x)=x^2+x+1$ is one-one function not an onto function.

Functions exercise 2.1 question 4

$f:A \rightarrow A$ is neither one-one nor onto.
Given:
$A=\{-1,0,1\} \text { and } f=\{(x, x): x \in A\}$
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
We need to prove that $f:A \rightarrow A$ is neither one-one nor onto.
First of all we check the function with one-one,
$\begin{aligned} &\begin{gathered} f(x)=x^{2} \\ \text { If } x=1, f(1)=1^{2}=1 \\ \text { If } x=-1, f(-1)=(-1)^{2}=1 \end{gathered}\\ &\text { Here } f(1) \text { and } f(-1) \text { have the same image } 1 \text { . } \end{aligned}$
So,f is not one-one.
Now, we go for onto function,
Co-domain of $f=\left \{ 0,1 \right \}$
$\begin{aligned} &f(x)=x^{2} \\ &f(1)=1^{2}=1 \\ &f(-1)=(-1)^{2}=1 \\ &f(0)=0 \end{aligned}$
Range of $f =\left \{ -1,0.1 \right \}$
Codomain of $f\neq$ Range of $f$ . (both are not same)
Hence, f is not onto

Functions exercise 2.1 question 5 (i)

One-one but not onto.
Given:
$f:N \rightarrow N$ given by $f(x)=x^2$ .
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
For any function to be a bijective, the given function be one-one and onto.
Solution:
Let's start with the injection test.
Let x and y be any two elements in the domain(N) such that $f(x)=f(y)$
$\begin{aligned} &f(x)=x^{2}, f(y)=y^{2} \\ &f(x)=f(y) \\ &x^{2}=y^{2} \\ &x=y \end{aligned}$
Where x and y are in N , so we don’t get 1 value.
So,f is an injection.
Surjection test:
Let y be any element in the codomain (N) , such that $f(x)=y$ for some element x in N .
$f(x)=y$
$x^2=y$
$x=\pm \sqrt{y}$ which may not be in N
Example:
If $y=2, x=\pm \sqrt{2}$ which is not in N .
So,f is not a surjection.
The condition of bijection is as we know the function should be one-one and onto.
Hence for this, f is not bijection

Functions exercise 2.1 question 5 (ii)

Neither one-one nor onto.
Given:
$f:Z \rightarrow Z$ given by $f(x)=x^2$
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
For any function to be a bijective, the given function be one-one and onto.
Solution:
Let's start with the injection test.
Let x and y be any two elements in the domain (Z) such that $f(x)=f(y)$
$\begin{aligned} &f(x)=x^{2}, f(y)=y^{2} \\ &f(x)=f(y) \\ &x^{2}=y^{2} \\ &x=\pm y \end{aligned}$
Therefore,f is not an injection
Surjection test:
Let y be any element in the codomain (Z) , such that $f(x)=y$ for some element x in Z .
$f(x)=y$
$x^2=y$
$x=\pm \sqrt{y}$ which may not be in N
Example:
If $y=2, x=\pm \sqrt{2}$ which is not in N .
So,f is not a surjection.
The condition of bijection is as we know the function should be one-one and onto.
Hence for this, f is not bijection.

Functions exercise 2.1 question 5 (iii)

Injective but not surjective.
Given:
$f:N \rightarrow N$ given by $f(x)=x^3$ .
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
For any function to be bijective, the given function be one-one and onto.
Solution:
Let us check for the given function is injection, surjection and bijection.
Let's start with the injection test.
Let x and y be any two elements in the domain (N) such that $f(x)=f(y)$
$\begin{aligned} &f(x)=x^{3}, f(y)=y^{3} \\ &f(x)=f(y) \\ &x^{3}=y^{3} \\ &x=y \end{aligned}$
So,f is an injection
Surjection test:
Let y be any element in the codomain (N) , such that $f(x)=y$ for some element x in N .
$f(x)=y$
$x^3=y$
$x=\sqrt[3]{y}$ which may not be in N
So,f is not a surjection.
Here f is injective but not surjective, so the f is not a bijective.
The condition of bijection is as we know the function should be one-one and onto.
Hence for this, f is not bijection.

Functions exercise 2.1 question 5 (iv)

Injective but not surjective.
Given:
$f:Z \rightarrow Z$ given by $f(x)=x^3$
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
For any function to be a bijective, the given function be one-one and onto.
Solution:
Let us check for the given function is injection, surjection and bijection.
Let's start with the injection test.
Let x and y be any two elements in the domain (N) such that $f(x)=f(y)$
$\begin{aligned} &f(x)=x^{3}, f(y)=y^{3} \\ &f(x)=f(y) \\ &x^{3}=y^{3} \\ &x=y \end{aligned}$
So,f is an injection
Surjection test:
Let y be any element in the codomain (N) , such that $f(x)=y$ for some element x in N .
$f(x)=y$
$x^3=y$
$x=\sqrt[3]{y}$ which may not be in N
So,f is not a surjection.
Here f is injective but not surjective, so the f is not a bijection.
The condition of bijection is as we know the function should be one-one and onto.
Hence for this, f is not bijection.

Functions exercise 2.1 question 5 (v)

Neither an injection nor a surjection.
Given:
$f:R \rightarrow R$ , defined by $f(x)=\left | x \right |$ .
Hint:
Injective function means every element in the domain has a distinct image in the co-domain.
Surjective
function means every element in the co-domain has at least one pre image in the domain of function.
Bijection ⇒ Function should fulfill the injection, surjection condition.
Solution:
Let us check if the given function is injective, surjective, or bijective.
Injection:
Let x and y be any two elements in the domain (R) such that $f(x)=f(y)$
$\begin{aligned} &f(x)=|x|, f(y)=|y| \\ &x=\pm y \end{aligned}$
Therefore f is not an injection.
Surjection test:
Let y be any element in the codomain (R) , such that $f(x)=y$ for some element x in R .
$\begin{aligned} &f(x)=y \\ &|x|=y \\ &x=\pm y \in Z \end{aligned}$
Therefore, f is surjective.
Since f is not an injective , but surjective. So the f is not bijective.

Functions exercise 2.1 question 5 (vi)

Neither injective nor surjective.
Given:
$f:Z \rightarrow Z$ defined by $f(x)=x^2+x$ .
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
Bijective ⇒ Function should fulfill the injective, surjective condition.
Solution:
Let us check if the given function is an injective, surjective, bijective.
Injection:
Let x,y be any two elements in domain $f(x)=f(y)$ .
$f(x)=x^2+x, f(y )=y^2+y$
Here we cannot say that x=y.
For example,
$x=2$ and $y=-3$
Then $x^2+x=2^2+2 =6$
$y^2+y=(-3)^2-3 =6$
Therefore, we have two number 2 and -3 in the domain z whose image is same as 6.
So f is not an injective.
Surjection:
Let y be any element in co-domain (R) such that $f(x)=(y)$ for some element x in (R)
$f(x)=(y)$
$x^2+x=y$
Here we can’t say $x\in Z$ .
$\begin{aligned} &y=-4\\ &x^{2}+x=-4\\ &x^{2}+x+4=0 \text { , on solving this }\\ &x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \text { (formula) }\\ &a=1, b=1, c=4\\ &x=\frac{-1 \pm \sqrt{1^{2}-4 \cdot 1 \cdot 4}}{2 \cdot 1}\\ &x=\frac{-1 \pm \sqrt{-15}}{2 \cdot 1}\\ &x=\frac{-1 \pm i \sqrt{15}}{2 \cdot 1} \text { which is not in } Z \end{aligned}$
So, f is not surjective and f is not a bijective.

Functions exercise 2.1 question 5 (vii)

Bijective.
Given:
As $f:Z \rightarrow Z$ defined by $f(x)=x-5$
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
Bijection ⇒ Function should fulfill the injection, surjection condition.
Solution:
Injection test:
Let $x,y$ be any two elements in domain(Z) such that $f(x)=(y),f(x)=x-5,f(y)=y-5$
$f(x)=f(y)$
$x-5=y-5$
$x=y$
So, f is an injection.
Surjection test:
Let y be any element in the co-domain(Z) such that $f(x)=y$ for some element x in Z( domain)
$f(x)=y$
$x-5=y$
$x=y+5$ which is in Z.
So, Z is a surjection and f is a bijection.

Functions exercise 2.1 question 5 (viii)

Neither injective nor surjective.
Given:
$f:R \rightarrow R$ defined by $f(x)=\sin x$ .
Hint:
One-one function means every element in the domain has a distinct image in the co-domain.
Onto function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Injection test
Let x and y be any two elements in the domain (R) such that $f(x)=f(y)$
$\sin x=\sin y$
Here x may not be equal to y because $\sin 0 = \sin \pi =0$
So, f is not an injection.
Surjection test:
Range of $f=[-1,1]$
Co-domain of $f=R$
Both are not the same.
So f is not a surjection and f is not a bijection

Functions exercise 2.1 question 5 (ix)

Bijective
Given:
$f:R \rightarrow R$ defined by $f(x)=x^3+1$ .
Hint:
Bijection: function should be one-one and onto function.
Solution:
Injection test:
Let x and y be any two elements in the domain (R) such that $f(x)=f(y)$
$x^3+1=y^3+1$
$x^3=y^3$
$x=y$
So, f is an injection.
Surjection test:
Let y be any element in the codomain (N) , such that $f(x)=y$ for some element x in R .
$f(x)=y$
$x^3 +1=y$
$x^3 =y-1$
$x=\sqrt[3]{(y-1)}\in R$
So, f is a surjection.
So, f is a bijection.

Functions exercise 2.1 question 5 (x)

Surjective but not injective
Given:
$f:R \rightarrow R$ , defined by $f(x)=x^3-x$
Hint:
Injective function means every element in the domain has a distinct image in the co-domain.
surjective function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Injective test:
Let x and y be any two elements in the domain (R), such that
$f(x)=f(y)$
$x^3-x=y^3-y$
Here we cannot say $x=y$
For example $x=1, y=1$
$x^3-x=1-1=0$
$y^3-y=(-1)^3-(-1)= -1+1=0$
So, -1 and 1 have the same image 0.
Thus f is not an injection.
Surjection test:
Let x and y be any two elements in the domain (R) such that $f(x)=f(y)$ for some element (R) in R.
$f(x)=f(y)$
$x^3-x=y$
In order to identity surjection,
$\begin{aligned} &f(x)=x^{3}-x \\ &f^{\prime}(x)=3 x^{2}-1=0 \\ &x=\pm \frac{1}{\sqrt{3}} \end{aligned}$
Therefore, f is a surjective.
Therefore, f is not a bijective.

Functions exercise 2.1 question 5 (xi)

Neither injective nor surjective.
Given:
$f:R \rightarrow R$ defined by $f(x)=\sin ^{2}x+\cos ^2x$ .
Hint:
Injective (one-one): function means every element in the domain has a distinct image in the co-domain.
Surjective(Onto): function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Injection condition:
$f(x)=\sin ^{2}x+\cos ^2x$
$\sin ^{2}x+\cos ^2x=1$ ( by formula)
So, $f(x)=1$ for every x in R.
For all elements in the domain the image is 1. So,f is not an injective.
Surjection:
Range of $f=\left \{ 1 \right \}$ , co-domain of f=R
Both are not the same.
So, f is not a surjection and f is not a bijection.

Functions exercise 2.1 question 5 (xii)

Injective but not surjective
Given:
$f: Q-\{3\} \rightarrow Q, \text { defined by } f(x)=\frac{2 x+3}{x-3}$
Hint:
Injective (one-one): function means every element in the domain has a distinct image in the co-domain.
Surjective(Onto): function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Injection:
let x,y be any two elements in the domain $\left ( Q-\{3\} \right )$ , such that $f(x)=f(y)$ .
$\begin{aligned} &f(x)=\frac{(2 x+3)}{(x-3)}, f(y)=\frac{(2 y+3)}{(y-3)} \\ &f(x)=f(y) \\ &\frac{(2 x+3)}{(x-3)}=\frac{(2 y+3)}{(y-3)} \\ &\begin{array}{l} (2 x+3)(y-3)=(2 y+3)(x-3) \\ 2 x y-6 x+3 y-9=2 x y-6 y+3 x-9 \\ 9 x=9 y \\ x=y \end{array} \end{aligned}$
So, f is an injection.
Subjection test:
Let y be any element in the co-domain Q, such that $f(x)=y$ for some element x in ( $\left ( Q-\{3\} \right )$ (domain).
$\begin{aligned} &f(x)=y\\ &\frac{(2 x+3)}{(x-3)}=y\\ &2 x+3=x y-3 y\\ &2 x-x y=-3 y-3\\ &x(2-y)=-3(y+1)\\ &x=-3(y+1) /(2-y), \text { which is not defined at } y=2 \end{aligned}$
So, f is not surjective.
Therefore, f is not bijective

Functions exercise 2.1 question 5 (xiii)

Injective
Given:
$f:Q\rightarrow Q$ defined by $f(x)=x^3+1$
Hint:
Injective (one-one): function means every element in the domain has a distinct image in the co-domain.
Surjective(Onto): function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Injection: Let x,y be any two element in the domain Q,
such that $f(x)=f(y)$ .
$\begin{aligned} &x^{3}+1=y^{3}+1 \\ &x^{3}=y^{3} \\ &x=y \end{aligned}$
Therefore, f is an injection.
Surjection: Let y be any two element in the co-domain Q, such that $f(x)=y$ for some element x in Q.
$\begin{aligned} &f(x)=y \\ &x^{3}+1=y \\ &x^{3}=y-1 \\ &x=\sqrt[3]{(y-1)} \end{aligned}$ which may not be Q.
So, f is not surjective.
Therefore, f is not bijective.

Functions exercise 2.1 question 5 (xvi)

Bijective
Given:
$f:R \rightarrow R$ , defined by $f(x)=5x^3+4$
Hint:
Bijective function should be one-one and onto function.
Solution:
Let x and y be any two elements in the domain(R), such that $f(x)=f(y)$ .
$\begin{aligned} &\Rightarrow 5 x^{3}+4=5 y^{3}+4 \\ &\Rightarrow 5 x^{3}=5 y^{3} \\ &\Rightarrow x^{3}=y^{3} \\ &\Rightarrow x=y \end{aligned}$
So, f is an injection.
Subjection test:
Let y be any element in the co-domain(R), such that $f(x)=y$ .
$\begin{aligned} &5 x^{3}+4=y \\ &x^{3}=\frac{(y-4)}{5} \in R \end{aligned}$
So, f is a surjective.
Hence, f is a bijective.

Functions exercise 2.1 question 5 (xv)

Bijective
Hint:
$f:R \rightarrow R$ , defined by $f(x)=3-4x$ .
Hint:
Bijective function should be one-one and onto function.
Solution:
Let
$\begin{aligned} &x_{1}, x_{2} \in R \\ &f\left(x_{1}\right)=3-4 x_{1}, f\left(x_{2}\right)=3-4 x_{2} \\ &f\left(x_{1}\right)=f\left(x_{2}\right) \\ &3-4 x_{1}=3-4 x_{2} \\ &x_{1}=x_{2} \end{aligned}$
Hence f is an injective.
Subjection test:
Let
$\begin{aligned} &y=3-4 x\\ &x=\frac{3-y}{4}\\ &\therefore\\ &\forall y \in R, \exists \frac{3-y}{4} \in R\\ &f\left(\frac{3-y}{4}\right)=3-4\left(\frac{3-4}{4}\right)=y \end{aligned}$
$\therefore f$ is onto
Hence, f is bijection.

Functions exercise 2.1 question 5 (xvi)

Neither injective nor surjective.
Given:
$f:R \rightarrow R$ defined by $f(x)=1+x^2$
Hint:
Injective (one-one): function means every element in the domain has a distinct image in the co-domain.
Surjective(Onto): function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Injection condition:
Let x,y be any two elements in domain R such that
$\begin{aligned} &f(x)=f(y), f(x)=1+x^{2}, f(y)=1+y^{2} \\ &1+x^{2}=1+y^{2} \\ &x^{2}=y^{2} \\ &x=\pm y \end{aligned}$
Therefore, f is not an injection.
Surjection test:
Let y be any two elements in domain (R) such that $f(x)=y$ for some element x in R.
$\begin{aligned} &f(x)=y \\ &1+x^{2}=y \\ &x^{2}=y-1 \\ &x=\sqrt[2]{(y-1)} \\ &\text { For, } y=O \in R \\ &x=\pm \sqrt{-1}=\pm i \text { is not in } R \text { . } \end{aligned}$
So, f is not a surjection and f is not a bijection

Functions exercise 2.1 question 5 (xvii)

Neither injective nor surjective.
Given:
$f:R \rightarrow R$ defined by $f(x)=\frac{x}{1+x^2}$
Hint:
Injective (one-one): function means every element in the domain has a distinct image in the co-domain.
Surjective(Onto): function means every element in the co-domain has at least one pre image in the domain of function.
Solution:
Let x and y be any two elements in domain (R), such that f(x) = f(y).
$\frac{x}{1+x^2} = \frac{y}{1+y^2}$
xy²+ x = x²y + y
xy² − x²y + x − y = 0
−xy(−y + x) + 1(x − y) = 0
(x − y) (1 – xy) = 0
x = y or x = $\frac{1}{y}$
So, f is not an injection.
Surjection test:
Let y be any element in co-domain (R), such that f(x) = y for some element x in R (domain).
f(x) = y
$\frac{x}{1+x^2} = y$
yx² – x + y = 0
x((-1) ± √(1 - 4x²))/(2y) if y ≠ 0
= (1 ± √(1 - 4y²))/(2y), which may not be in R
For example, if y = 1, then (1 ± √(1-4))/(2y) = (1 ± i√3)/2, which is not in R Therefore, f is not surjection and f is not bijection.

Functions exercise 2.1 question 6

One
Given:
$F:A\rightarrow B$ is an injection such that the range of $f=\left \{ a \right \}$
Hint:
For an injection there will be exactly one image for each element.
Solution:
Here $f=\left \{ a \right \}$
⇒ Since F is an injection, there will be exactly one image for each element of f.
⇒ So, the number of images of f is one.
$\therefore$ Number of element in A is one.

Functions exercise 2.1 question 7

Given:

Hint:

For a bijection, we have to prove that this function is one-one and onto

Solution:

Let and

Consider the function

Here

For one-one function, we have

So,is a one-one function.

For onto function, we have

Again here

Substituting the value ofin

is onto function.

Hence is bijective.

Note:

If any function is bijective, then it is invertible.

Functions exercise 2.1 question 8 (i)

f is not bijective.
Given:
$f:A \rightarrow A$ , given by $f(x)=\frac{x}{2}$
To prove:
Here we have to show that the given function is one-one and onto.
Solution:
For one-one:
Let $x_1$ and $x_2$ be any two elements in the domain A, such that
$\begin{aligned} & f\left(x_{1}\right)=f\left(x_{2}\right) \\ \Rightarrow & \frac{x_{1}}{2}=\frac{x_{2}}{2} \\ \Rightarrow & x_{1}=x_{2} \end{aligned}$
So,f is one-one.
For onto:
Let y be any element in the codomain A, such that $f(x)=(y)$ for some element x in domain A
Then, $f(x)=(y)$
$\Rightarrow \frac{x}{2}=y$ $\left [ f(x)=\frac{x}{2} \right ]$
$\Rightarrow x=2y$ , which may not be in A=[-1, 1]
So f is not onto.
Hence,f is not bijective.

Functions exercise 2.1 question 8 (ii)

f is not bijective
Given:
$g:A \rightarrow A$ , given by $g(x)=\left | x \right |$
To prove:
Function f is one-one, onto or bijective.
Hint:
For any function to be a bijective, the given function should be one-one and onto.
Solution:
First we will check whether the given function is one-one or not.
We know for one-one function
$\begin{aligned} &\Rightarrow \quad g\left(x_{1}\right)=g\left(x_{2}\right) \\ &\Rightarrow \quad\left|x_{1}\right|=\left|x_{2}\right| \\ &\Rightarrow \quad x_{1}=\pm x_{2} \end{aligned}$
So, g is not one-one.
$g(x)=\left | x \right |$
Let $g(x)=y$ such that $y \in A$
$y=|x|$
Hence, the value of y is defined only if y is positive,
But y is a real number
Hence, if y is negative, there is not corresponding element of x
i.e; $y=-x$ , there is no value of x inA
Hence, f is not onto.
So, g is not onto.
Hence g is not bijective.

Functions exercise 2.1 question 8 (iii)

f is not bijective.
Given:
$h:A\rightarrow A$ , given by $h(x)=(x)^2$
To prove:
Function h is one-one, onto or bijective.
Hint:
For any function to be bijective, the given function should be one-one and onto.
Solution:
First we will check whether the given function is one-one or not.
We know for function h to be one-one
$\begin{aligned} &\begin{aligned} & h\left(x_{1}\right)=h\left(x_{2}\right) \\ \Rightarrow & x_{1}^{2}=x_{2}^{2} \\ \Rightarrow & x_{1}=\pm x_{2} \end{aligned}\\ &\text { So, } h \text { is not one-one. } \end{aligned}$
$h(x)=x^2$
Let $h(x)=y$ such that $y \in A$
$y=x^2$
Hence, the value of y is defined only if y is positive,
But y is a real number
Hence, if y is negative, there is not corresponding element of x
i.e; for $y=-1$ , there is no value of x in A.
Hence, h is not onto.
Hence, h is not bijective.

Functions exercise 2.1 question 9 (i)

f is surjective.
Let $f=\left \{ \left ( x,y \right ) \right \}:x$ is a person, y is the mother of x
Hint:
As for each element x in the domain set, there is a unique element y in the co-domain set.
So, f is a function.
Solution:
First we check for injection or one-one.
We know: For one-one,for each element x in the domain set, there should be a unique element y in the co-domain set.
But here,y can be the mother of two or more persons.
So, f is not injective.
Again for surjective,
For every mother y defined by (x,y) , there exists a person x for whom y is mother.
So, f is surjective.
Hence, f is surjective function.

Functions exercise 2.1 question 9 (ii)

Let $g:\left \{ \left ( a,b \right ) \right \}:a$ is person and b is an ancestor of a
To prove:
The mapping is injective, surjective or not.
Hint:
As for each element x in the domain set, there is a unique related element y in the co-domain set.
So, f is a function.
Solution:
Since the ordered map (a,b) is not a map because "a" can have many ancestors. So the codomain set is not unique.
So, g is not a function.
Note:
If the function does not exist then we can’t show that the function is an injective or surjective.

Functions exercise 2.1 question 10

Given $A= \left \{ 1,2,3 \right \}$
Number of element in A =3
We know that,
Number of one-one function

number of ways of arranging 3 elements.
=3! = 6
Hence, the number of one-one function as following:
$\\(i) \{(1,1),(2,2),(3,3)\}\\ (ii) \{(1,1),(2,3),(3,2)\}\\ (iii) \{(1,2),(2,1),(3,3)\}\\ (iv) \{(1,2),(2,3),(3,1)\}\\ (v) \{(1,3),(2,2),(3,1)\}\\ (vi) \{(1,3),(2,1),(3,2)\}\\$

Functions exercise 2.1 question 11

f is bijection.
Given:
$f:R \rightarrow R$ is a function defined by $f(x)=4x^3+7$ .
To prove:
f is bijection.
Hint:
Any function to be bijection. The given function should be one-one and onto.
Solution:
First we will check whether the function is one-one or not.
Let x and y be any two element in the domain R such that
$\begin{aligned} & f(x)=f(y) \\ \Rightarrow & 4 x^{3}+7=4 y^{3}+7 \\ \Rightarrow & \quad 4 x^{3}=4 y^{3} \\ \Rightarrow & x^{3}=y^{3} \\ \Rightarrow & x=y \end{aligned}$
So, f is one-one.
Now, we will check if the given function is onto or not.
Let y be any element in the co-domain R such that $f(x)=y$ for some element x in R (domain).
$f(x)=y$
$\begin{aligned} &\Rightarrow \quad 4 x^{3}+7=y \\ &\Rightarrow \quad 4 x^{3}=y-7 \\ &\Rightarrow \quad x=\sqrt[3]{y-7} \end{aligned}$
So, for every element in the co-domain there exists some pre-image in the domain.
So, f is onto.
Hence f is bijection.

Functions exercise 2.1 question 12

Given:
$f:R \rightarrow R$ , given by $f(x)=e^x$ .
To prove:
f is one-one but not onto.
Hint:
If different element in A have distinct images in B then the function is one-one and if every element in B has at least one pre-image in A then the function is onto.
Solution:
First we will check whether the function is one-one or not.
Here, let $x,y \in R$ such that
$f(x)=f(y)$
$\begin{array}{ll} \Rightarrow & e^{x}=e^{y} \\ \Rightarrow & e^{x-y}=1=e^{0} \\ \Rightarrow & x-y=0 \\ \Rightarrow & x=y \end{array}$
$\therefore f$ is one-one
Now, we check onto
$f(x)=e^x$
Let $f(x)=y$ such that $y \in R$
$y=e^x$
clearly the range of $e^{x} \text { is }(0, \infty)=R^{+}$ but the given range isR
co-domain≠ Range
$\therefore f$ is not onto.
Note:
When co-domain is replaced by $R_0^+$ , i.e. $(0, \infty)$ then f become onto function.

Functions exercise 2.1 question 13

Given:
$f:R_0^+\rightarrow R$ given by $f(x)\log _ax:a >0$ .
To prove:
$f(x)\log _ax:a$ is bijection.
Hint:
For any function to be bijective, the function should be one-one and onto.
Solution:
Let $x,y \in R_0^+$ such that
$f(x)=f(y)$
$\begin{array}{ll} \Rightarrow & \log _{a} x=\log _{a} y \\ \Rightarrow & \log _{a} \frac{x}{y}=0 \\ \Rightarrow & \frac{x}{y}=1 \\ \Rightarrow & x=y \end{array}$
$\therefore f$ is one-one.
Now, let $y\in R$ be arbitrary then
$f(x)=y$
$\begin{aligned} &\Rightarrow \quad \log _{a} x=y \\ &\Rightarrow \quad x=a^{y} \in R_{0}^{+} \\ &{\left[\because a>0 \Rightarrow a^{y}>0\right]} \end{aligned}$
Thus for all $y\in R$ , there exist $x=a^y$ such that $f(x)=y$ .
$\therefore f$ is onto
$\therefore f$ is one-one and onto.
Hence f is bijective.

Functions exercise 2.1 question 14

Given:
$A=\left \{ 1,2,3 \right \}$
To prove:
One-one function must be onto.
Solution:
Here $f:A\rightarrow A$ and $A=\left \{ 1,2,3 \right \}$
We know that, since f is one-one, so the three elements of $\left \{ 1,2,3 \right \}$ must be taken to different element of the co-domain $\left \{ 1,2,3 \right \}$ under f.
Hence f must be onto.

Functions exercise 2.1 question 15

Given:
$f:A\rightarrow A$ , given by $A=\left \{ 1,2,3 \right \}$ .
To prove:
Onto function must be one-one.
Solution:
Let f is not one-one then there exists two elements say 1 and 2 in the domain having same image in the co-domain.
Also, the image of 3 under f can be only one element.
$\therefore$ The range set will have at most two element of the co-domain, but we know that in the range set we have three elements $\left \{ 1,2,3 \right \}$ .
i.e. There arises a contradiction that f is not onto function.
Hence f must be one-one.

Functions exercise 2.1 question 16

Given:
Here given that $\left \{ 1,2,3....n \right \}$ is the set.
Here we have find all onto function from the given set.
Hint:
Since if f is onto then all element have a unique pre image.
Solution:
Taking the set $\left \{ 1,2,3 \right \}$
$\therefore$ Total number of one-one function $3\times 2\times 1=6$
As example since f is onto, all elements of $\left \{ 1,2,3 \right \}$ have unique pre-image

Element	Number of possible pairs
1	3
2	2
3	1

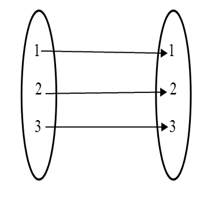
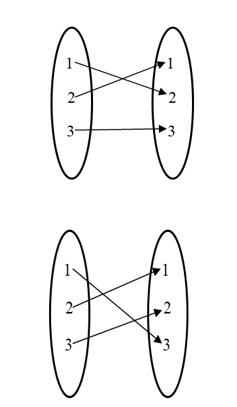
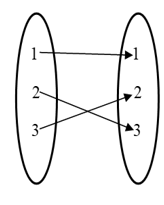
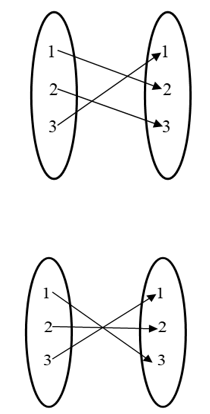
So as the diagram, we get

Elements	Number of possible pairs
1	n
2	n-1
3	n-2
.	.
.	.
n-1	.
n	2
	1

So as the diagram, we get $n \times(n-1) \times(n-2) \times \ldots \times 2 \times 1=n !$

Functions exercise 2.1 question 17

Let $f_1:R\rightarrow R$ and $f_2:R\rightarrow R$ be two function given by
$f_1(x)=x$
$f_2(x)=x$
We can easily verify that $f_1$ and $f_2$ are one-one functions.
Now,
$\left(f_{1}+f_{2}\right) x=f_{1}(x)+f_{2}(x)=x-x=0$
$\therefore f_1+f_2:R\rightarrow R$ is a function given by $(f_1+f_2)x=0$
Since $f_1+f_2$ is a constant function.
Hence it is not one-one.:

Functions exercise 2.1 question 18

Answer:

Let $f_1:Z\rightarrow Z$ defined by $f_1(x)=x$ and $f_2:Z\rightarrow Z$ defined by $f_2(x)=-x$
Then $f_1$ and $f_2$ are surjective functions.
Now,
$f_1+f_2:Z\rightarrow Z$ is given by
$\begin{aligned} \left(f_{1}+f_{2}\right)(x) &=f_{1}(x)+f_{2}(x) \\ &=x-x \\ &=0 \end{aligned}$

Since $f_1+f_2$ is a constant function.
Hence it is not surjective.

Functions exercise 2.1 question 19

Given:
$f_1$ and $f_2$ are one-one mapping.
To prove:
The product $f_1 \times f_2$ is not one-one.
Solution:
Let $f_1:R\rightarrow R$ be defined by $f_1(x)=x$
and $f_2:R\rightarrow R$ be defined by $f_2(x)=x$
Clearly $f_1$ and $f_2$ are one-one functions.
Now, $F= f_1\times f_2:R\rightarrow R$ is defined by
$F(x)=\left(f_{1} \times f_{2}\right)(x)=f_{1}(x) \times f_{2}(x)=x^{2}$ …(i)
Clearly $F(-1)=1=F(1)$
since the two elements have the same image.
$\therefore F$ is not one-one.
Hence $f_1 \times f_2$ is not one-one.

Functions exercise 2.1 question 20

Let $f_1:R\rightarrow R$ and $f_2:R\rightarrow R$ are two function defined by $f_1(x)=x^2$ and $f_2(x)=x$ .
Clearly $f_1$ and $f_2$ are one-one functions.
Now, $\frac{f_1}{f_2}:R\rightarrow R$ given by
$\left(\frac{f_{1}}{f_{2}}\right) x=\frac{f_{1}(x)}{f_{2}(x)}=x^{2} \vee x \in R$
Let $\frac{f_1}{f_2}=f$
$\therefore f= R\rightarrow R$ defined by $f(x)=x^2$
Now, $f(-1)=1=f(1)$
since, the two elements have the same image.
$\therefore f$ is not one-one.
Hence, $\frac{f_1}{f_2}:R\rightarrow R$ is not one-one.

Functions exercise 2.1 question 21 (i)
Answer:

$f=(2,5),(3,7),(4,6)$
Given:
Here given that
$A= \left \{ 2,3,4 \right \}$ and $A= \left \{ 2,5,6,7 \right \}$
Here we have to construct an example of injective.
Hint:
For injective, we have to construct the example of one-one function.
Solution:
Here $A= \left \{ 2,3,4 \right \}$ and $A= \left \{ 2,5,6,7 \right \}$
Hence for injective (i.e) one-one.
$f=(2,5),(3,7),(4,6)$
Hence the result.

Functions exercise 2.1 question 21 (ii)

Answer:

$f=(2,2),(5,3),(6,4),(7,4)$
Given:
Here given that
$A= \left \{ 2,3,4 \right \}$ and $A= \left \{ 2,5,6,7 \right \}$
Here we have to construct an example as the mapping from A to B which is not injective.
Hint:
In this question we construct an example of many one function.
Solution:
Here $A= \left \{ 2,3,4 \right \}$ and $A= \left \{ 2,5,6,7 \right \}$
Hence we have
$g=(2,2),(3,5),(4,2)$
It is many-one.

Functions exercise 2.1 question 21 (iii)
Answer:

Given: Here given that
$A= \left \{ 2,3,4 \right \}$ and $A= \left \{ 2,5,6,7 \right \}$
Here we have to find a mapping from A to B.
Solution:
Here $A= \left \{ 2,3,4 \right \}$ and $A= \left \{ 2,5,6,7 \right \}$
$h=(2,2),(5,3),(6,4),(7,4)$
This is the required mapping.

Functions exercise 2.1 question 22

Answer:

Let $f:R\rightarrow R$ given by $f_1(x)=x-[x]$
To prove:
The given function is neither one-one nor onto.
Solution:
First we will check whether the given function is one-one or not.
For one-one; we have,
$\therefore f(x)=x-[x]$
$\Rightarrow f(x)=0$ for all $x\in R$
$\therefore f$ is not one-one where as many-one.
Again, Range $(f)=[0,1) \neq R$
$\therefore f$ is not onto.
Hence f is neither one-one nor onto

Functions exercise 2.1 question 23
Answer:

Given:
$f(n)=\left\{\begin{array}{ll} n+1, & \text { if } n \text { is odd } \\ n-1, & \text { if } n \text { is even } \end{array}\right.$
To prove:
Function f is bijection.
Hint:
For any function to be a bijection, the given function should be one-one and onto.
Solution:
Here $f:N \rightarrow N$
First we will check whether the given function is one-one or not.
For one-one,
Case I : If n is odd
Let $x,y\in N$ such that $f(x)=f(y)$
As $f(x)=f(y)$
$\begin{array}{ll} \Rightarrow & x+1=y+1 \\ \Rightarrow & x=y \end{array}$
Case II : If n is even
Let $x,y\in N$ such that $f(x)=f(y)$
As $f(x)=f(y)$
$\begin{array}{ll} \Rightarrow & x-1=y-1 \\ \Rightarrow & x=y \end{array}$
So, f is injective (one-one).
Again we will check whether the given function is onto or not.
For onto,
Case I : If n is odd
As for every $f:N \rightarrow N$ , $n \in N$ , there exists $y=n-1$
$f(y )=f(n-1)$
$=n-1+1$
$=n$
Case II : If n is even
As for every $n \in N$ , there exists $y=n+1$
$\Rightarrow f(y)=f(n+1)=n+1-1=n$
So f is surjective (onto).
Hence f is a bijection.

Here are some commonly known benefits and features of using the RD Sharma Class 12 chapter 1 exercise 2.1 solutions:-

Best Study Guide Created By Experts

Class 12 RD Sharma chapter 1 exercise 2.1 solution can be an excellent study guide for students who have difficulty understanding concepts in class. These solutions are crafted by experts and will help them to solve the questions and teach them about various tips and tricks that might be beneficial for answering exam questions.

Homework Solutions

Most school teachers use the NCERT books to give students homework, which means the RD Sharma class 12th exercise 2.1 will be excellent when solving homework questions. The RD Sharma class 12 solutions chapter 1 ex 2.1 is regularly updated with all the latest information, and they correspond to all the chapters in the NCERT book.

Best For Self-Study And Exam Preparation

In class 12, students need to conduct and follow self-study sessions to improve and test their knowledge of their subjects. For exam preparation and home practice without any tuition teacher, using RD Sharma class 12 chapter 1 exercise 2.1 will be highly beneficial for them. Students will be able to practice their NCERT questions at home and look up answers from RD Sharma class 12 solutions Functions ex 2.1 to check their progress and knowledge on the subject.

One-Stop Solution With Zero Investment

While most NCERT solutions and tuition costs a lot of money, the RD Sharma 12 solutions Functions ex 2.1 is completely free of cost. They are easily available on Career360 in pdf form and can be downloaded anytime you want. RD Sharma class 12th exercise 2.1 on Career360 will be the one-stop destination for NCERT solutions.

Trusted By Thousands Of Students

RD Sharma class 12th exercise 2.1 is well-known for its solutions, and thousands of students have trusted them and received good results. Students and teachers have also found that the questions from the book often appear in board exams, so they highly recommend using these books for self-study and exercise solutions. RD Sharma class 12 solutions Functions ex 2.1 has become one of the most acclaimed NCERT solutions that you will find online.

More About The Exercise

The class 12 RD Sharma chapter 1 exercise 2.1 solution has the Functions chapter. It is the second chapter in the book and needs special attention from students due to its complex nature. The concepts discussed include identity function, constant function, polynomial function, signum function, etc. The exercise will explore questions from these parts and contains a total of 45 questions on two levels.

Chapter-wise RD Sharma Class 12 Solutions

Frequently Asked Questions (FAQs)

1. How can class 12 RD Sharma chapter 1 exercise 2.1 solution be helpful for students?

The second chapter in the Mathematics book of class 12 deals with Functions that you have learned in the previous class. The class 12 RD Sharma chapter 1 exercise 2.1 solution will help you to solve these questions and provide you with a clear understanding of how you must do the calculations.It will be of great help to students in exam preparations for both school and board exams.

2. Is RD Sharma class 12 solutions Functions ex 2.1 set according to the latest syllabus?

The RD Sharma 12 solutions Functions ex 2.1 is always kept up to date with the latest syllabus in the NCERT book. With every new edition of the NCERT book, the pdf of the RD Sharma 12 solutions chapter 1 ex 2.1 is also updated so that students will find answers to all the questions in the book.

3. Can I use RD Sharma class 12th exercise 2.1 for my exam preparations?

The RD Sharma Sharma class 12 chapter 1 exercise 2.1 is a highly acclaimed NCERT solution for class 12 students. The answers and explanations provided in the book have some unique tips and tricks that will help you solve questions easier and faster than others.

4. Do I have to buy the RD Sharma class 12 chapter 1 exercise 2.1 book?

You don't need to buy the RD Sharma class 12 chapter 1 exercise 2.1 book at all. The pdf of the book is easily available online. You can download it anytime you want and save it on your electronic devices. Moreover, the pdf is available completely free of cost, so you don't have to make any financial investment.

5. How can the Class 12 RD Sharma chapter 1 exercise 2.1 solution be beneficial for me?

The Class 12 RD Sharma chapter 1 exercise 2.1 solution book will be quite helpful for students who want to score well in their exams and have started preparing in advance. It can also be used for self-testing, self-practice, and understanding your weak points. The book is trusted by many students and teachers, which again shows that it can help you with exam preparation