ICSE 10 Maths Question Paper 2025 (All Sets) - Paper Analysis, Difficulty Level, Students Reaction

Question 1: The given quadratic equation $3 x^2+\sqrt{7} x+2=0$ has:
(a) two equal real roots.
(b) two distinct real roots.
(c) more than two real roots.
(d) no real roots.

Solution:

To determine the nature of the roots of the quadratic equation:

$
3 x^2+\sqrt{7} x+2=0
$

we use the discriminant method. The discriminant $\Delta$ of a quadratic equation $a x^2+b x+c=0$ is given by:

$
\Delta=b^2-4 a c
$

For our given equation:
- $a=3$,
- $b=\sqrt{7}$,
- $c=2$.

Now, compute the discriminant:

$
\begin{gathered}
\Delta=(\sqrt{7})^2-4(3)(2) \\
=7-24 \\
=-17
\end{gathered}
$

Since the discriminant is negative ( $\Delta<0$ ), the quadratic equation has no real roots (it has two complex conjugate roots instead).

Thus, the correct answer is:

$
(d) \text { no real roots. }
$

Question 2: Mr. Anuj deposits $\mathbf{ 5 0 0}$ per month for $\mathbf{1 8}$ months in a recurring deposit account at a certain rate. If he earns ₹ 570 as interest at the time of maturity, then his matured amount is:

(a) $(500 \times 18+570)$
(b) $(500 \times 19+570)$
(c) $(500 \times 18 \times 19+570)$
(d) $(500 \times 9 \times 19+570)$

Solution:

$\begin{aligned}
M \cdot V & =P*{n}+I \\
& =500 \times 18+570
\end{aligned}$

Correct answer: Option (a)

Question: The equation of the line passing through the origin and parallel to the line $3 x+4 y+7=0$ is:
(a) $3 x+4 y+5=0$
(b) $4 x-3 y-5=0$
(c) $4 x-3 y=0$
(d) $3 x+4 y=0$

Solution:

The given line is $3 x+4 y+7=0$. A line parallel to it has the same form but without the constant term. Since it passes through the origin, the equation is:

$
3 x+4 y=0
$

So, the correct answer is:

$
(d) 3 x+4 y=0
$

Question: In the given diagram, chords $A C$ and $B C$ are equal. If $\angle A C D=12 \mathbf{0}^{\circ}$, then $\angle A E C$ is:

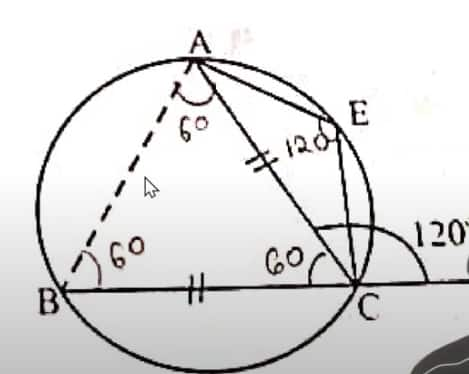
(a) $30^{\circ}$
(b) $60^{\circ}$
(c) $90^{\circ}$
(d) $120^{\circ}$

Question: A man invested in a company paying $12 \%$ dividend on its share. If the percentage return on his investment is $10 \%$, then the shares are:
(a) at par
(b) below par
(c) above par
(d) cannot be determined

Question: Statement 1: The point which is equidistant from three non-collinear points $D, E$ and $F$ is the circumcentre of the $\triangle D E F$.
Statement 2: The incentre of a triangle is the point where the bisector of the angles intersects.
(a) Both the statements are true.
(b) Both the statements are false.
(c) Statement 1 is true, and Statement 2 is false.
(d) Statement 1 is false, and Statement 2 is true.