HC Verma Concepts Of Physics: Every Student Must Attempt These 5 Problems

Updated on Apr 24, 2022 09:00 AM IST

HC Verma’s Physics textbook helps with developing problem-solving skills and enhancing the theoretical knowledge of students. This textbook improves students' understanding of various concepts related to physics, placing primary focus on conceptual clarity. Along with explaining the concepts, it also provides examples and questions belonging to easy, moderate and difficult levels. The questions are of the objective, long answer, short answer and comprehensive answer categories. Having the HC Verma book is an advantage for National Eligibility cum Entrance Test (NEET) and Joint Entrance Exam (JEE) Main aspirants.

HC Verma Concepts Of Physics: Every Student Must Attempt These 5 Problems

The units discussed in the HC Verma book are Thermodynamics, Modern Physics and Optics, Mechanics, Waves, Thermodynamics and Electromagnetism. Each chapter or unit has hundreds of questions. Here’s a look at five questions selected by Careers360:

Question 1: This deals with tension force and is from Mechanics. The problem is based on how much tension the tail of a monkey can hold.
Question 2: This is from the unit Waves which uses basic geometrical ideas to solve a problem from Constructive Interference.
Question 3: This is from Thermodynamics. The problem is to find heat generated in a liquid by a paddle wheel coupled to a mass.
Question 4: This problem is from Optics and Modern Physics. The question is based on Refraction. The problem is to find the height to which water is to be poured into a vessel to make a particle at the bottom of the container visible to an eye fixed at a corner of the vessel.
Question 5: This one asks the student to find the time period of oscillation of a charged block that undergoes elastic collision.

HC Verma Solutions

Given below are the solutions – “HCV solutions” as these are often described – to the five questions.

Question 1: Mechanics

Monkey B shown in the figure is holding on to the tail of monkey A, which is climbing up a rope. The masses of monkeys A and B are 5 kg and 2 kg respectively. If A can tolerate a tension of 30 N in its tail, what force should it apply on the rope in order to carry monkey B with it? Take g = 10 m/s2

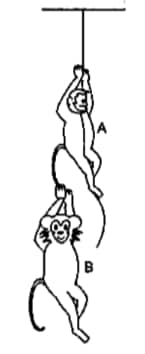Two Monkeys A And B

Solution:

Let T is the tension on the rope and T’ is the tension in the tail of monkey A.

The free body diagram of the monkey A and B are shown below

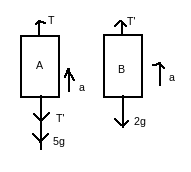Free Body Diagram Of A And B

From the free body diagram of B

T’+2a=2g

30=2g-2a

a=-5m/s2

From the free body diagram of A

T=T’+5g-5a

T=30+50+25=105N=Maximum value

For minimum value a=0, therefore T’=2g=20N

T=T’+5g=20+50=70N

Therefore a force between 70 and 105 is to be applied by the monkey A

Question 2: Waves

The figure shows two coherent sources S₁ and S₂ which emit sound of wavelength in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such a way that S₁S₂ lies in its plane and the middle point of S₁S₂ is at the centre of the wire. Find the angular position theta on the wire for which constructive interference takes place.

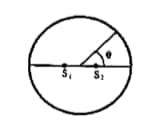Two Coherent Sources

Solution: Let O be the centre of the circle. Drop a perpendicular from P to the diameter=PM. Theta is the <POM.

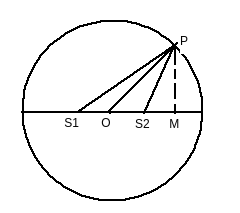Circular Wire

$\\OP=R\\OM=Rcos\theta\\$

$\\S1P^2-S2P^2=PM^2+S1M^2-[PM^2+S2M^2]\\=S1M^2-S2M^2\\=(1.5\lambda+Rcos\theta)^2-(Rcos\theta-1.5\lambda)^2=6\lambda Rcos\theta\\S1P^2-S2P^2=6\lambda Rcos\theta \\(S1P+S2P)(S1P-S2P)=6\lambda Rcos\theta\\2R(S1P-S2P)=6\lambda Rcos\theta\\(S1P-S2P)=3\lambda cos\theta$

$\text{For constrictive interference}\ S1P-S2P=n\lambda$

$\\3\lambda cos\theta=n\lambda$

$\\for\ n=1, \ \theta=70.5^o.\ n=2\ \theta=48.2^o. \\\ n=2\ \theta=0^o.\ n=0\ \theta=90^o$

$\\\text{Hence the constructive interference is for }\\ n=0^o, \ 48.2^o\ 70.5^o,\ 90^o......$

Question 3: Thermodynamics

Figure shows a paddle wheel coupled to a mass of 12kg through fixed frictionless pulleys. The paddle is immersed in a liquid of heat capacity 4200J/K kept in an adiabatic container. Consider a time interval in which the 12kg block falls slowly through 70cm. (a) How much heat is given to the liquid? (b) How much work is done on the liquid? (c) Calculate the rise in the temperature of the liquid neglecting the heat capacity of the container and the paddle.

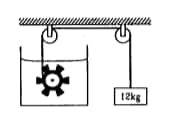Paddle Wheel

Solution: a) No heat is given to the liquid. As the mass moves down the mechanical work is converted into heat and no heat is given to the liquid.

b) Work done on the liquid = loss in potential energy by the mass=mgh

=12*10*0.7=84J

c) Potential energy(PE)= Heat generated=ms?t

It is asked to calculate the value of ?t,

Here the mass of the liquid in the container is not given. The heat generated is calculated for 1 Kg of liquid.

?t = PE/ms=84/(1*4200)=0.02K

Question 4: Optics And Modern Physics

A cylindrical vessel, whose diameter and height both are equal to 30 cm, is placed on a horizontal surface and a small particle P is placed in it at a distance of 5.0 cm from the centre. An eye is placed at a position such that the edge of the bottom is just visible (see figure). The particle P is in the plane of the drawing. Up to what minimum height should water be poured in the vessel to make the particle P visible?

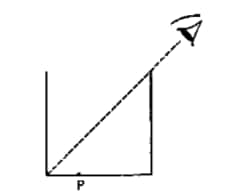Particle In Vessel

Solution:

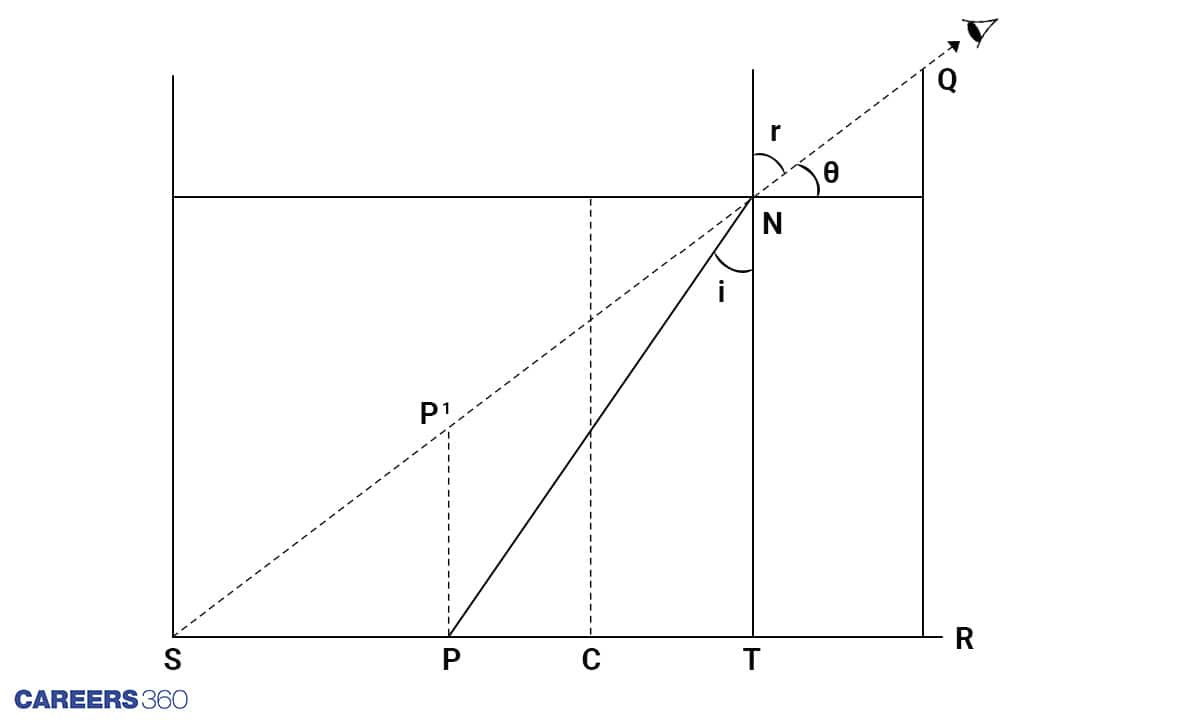Particle In Vessel Ray Diagram

SP=10cm, PC=5cm and let CT=x cm

sini/sinr=1/refractive index of water=3/4

$\\\theta=r=45^o(from \Delta SQR\ tan\theta=1)\\tanr=\frac{x+15}{d}\\r=45^o\\1=\frac{x+15}{d}\\x=d-15.....(1)\\\frac{sini}{sinr}=3/4(refractive\ index\ of \ water=4/3)\\sini=3/4,\ therefore \ tani=\frac{3}{\sqrt{23}}=0.625\\From \ figure\ tani=\frac{x+5}{d}\\So\ \frac{x+5}{d}=0.625\\from \ (1) x=d-15\\therefore\\\frac{d-10}{d}=0.625\\d=26.67cm$

So the height of the water from the bottom to be filled to see the point P is =26.67cm

Question 5: Electromagnetism

A block of mass m containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any) find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?

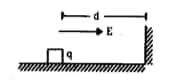Charge On Horizontal Table

Solution:

Displacement s=ut+0.5at². Since the initial velocity u=0, s=0.5at².

Here the acceleration a=Fe/m=qE/m and s=d.

∴ d=0.5qEt2/m or t=(2dm/qE)^0.5.

Time period=2t=2(2dm/qE)^0.5=(8dm/qE)^0.5s.

Since the acceleration is constant, the oscillatory motion is not simple harmonic. For simple harmonic motion, acceleration should be proportional to the displacement.