Physics: Projectile Motion That Won India An Olympic Gold

On August 7, 2021, when India's medal tally at the Tokyo Olympics 2020 was still short of gold, 23-year-old Neeraj Chopra bagged one ending India’s 121-year wait for an athletics medal on the world's top sporting stage.

Practically every Indian saw the video of the throw that won us the gold medal and the graphics featuring the javelin as a projectile became points of discussion on the streets. youths were able to relate to the science behind that throw and appreciate nuances like the angle of projection, sprint and body shape. As per the German biomechanical expert, Klaus Bartonietz, who trained the first ever Indian gold medallist in track and field, “Neeraj Chopra is not the strongest or the tallest but his supreme athleticism and elasticity make him a special talent”. Bartonietz further simplified his point by explaining that Chopra is the ‘dhanush’ (bow) and the javelin is the ‘arrow’.

This Story also Contains

1. Physics Behind The Javelin Throw
2. Angle Of Projection, Horizontal Range Of Projectile
3. Principle Of Physical Independence Of Motions
4. Horizontal range of projectile
5. Speed Of Projection And Rhythm

The javelin isn’t exactly new. Once, it was most familiar as a weapon, a version of the spear. The principal weaponry of the armies of the great Macedonian ruler and conqueror, Alexander, included the hoplite spear (8 feet) and sarissa (18-20 feet), both similar to the javelin but longer. It was an important weapon even in the classic Indian fourfold defence system. Javelin throw as a sport, however, was largely under-appreciated until Chopra.

But how does the javelin throw work exactly? This is an effort to explain the science, one of the concepts of physics, behind the javelin throw. To understand that, as well as Bartonietz’s bow-arrow analogy, let’s try to first understand projectile motion.

Projectile motion is the motion of an object thrown into space upon which the only acting force is gravity (if we neglect the air resistance). The object thrown is a “projectile” and the path it takes is called “trajectory”.

Here are some projectile motion examples:

• Firing a canon.

• Throwing a basketball at the basket

• Launching a missile

• Javelin throw

• Archery

• Water escaping a hose

• Car and bike stunts

• Cricket ball hit by the bat

Physics Behind The Javelin Throw

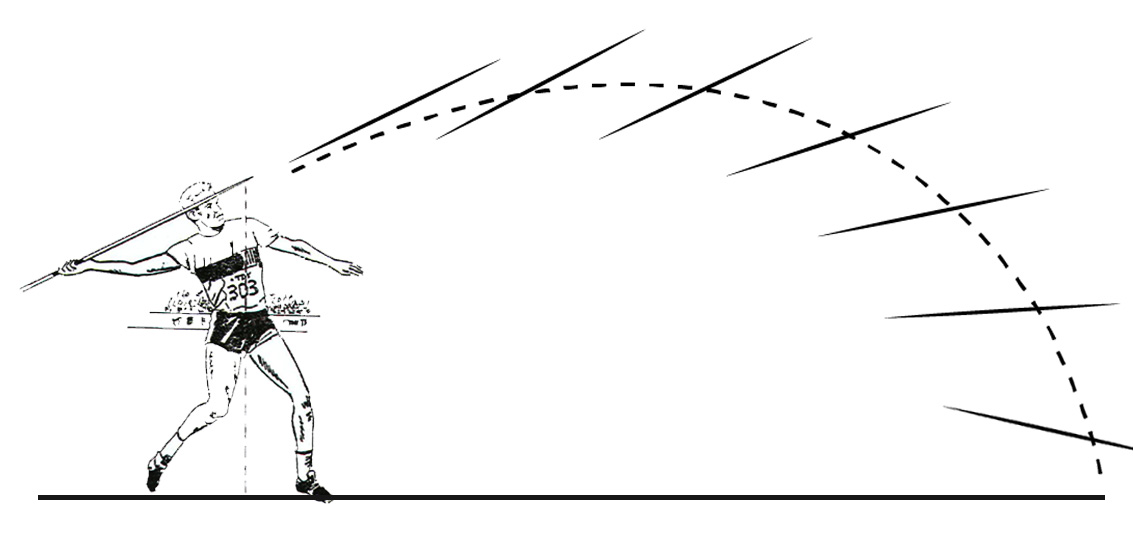
The illustrations below show how a javelin, once thrown, travels through air and how different angles of the throw will cause it to follow different paths or trajectories.

Angles of throw

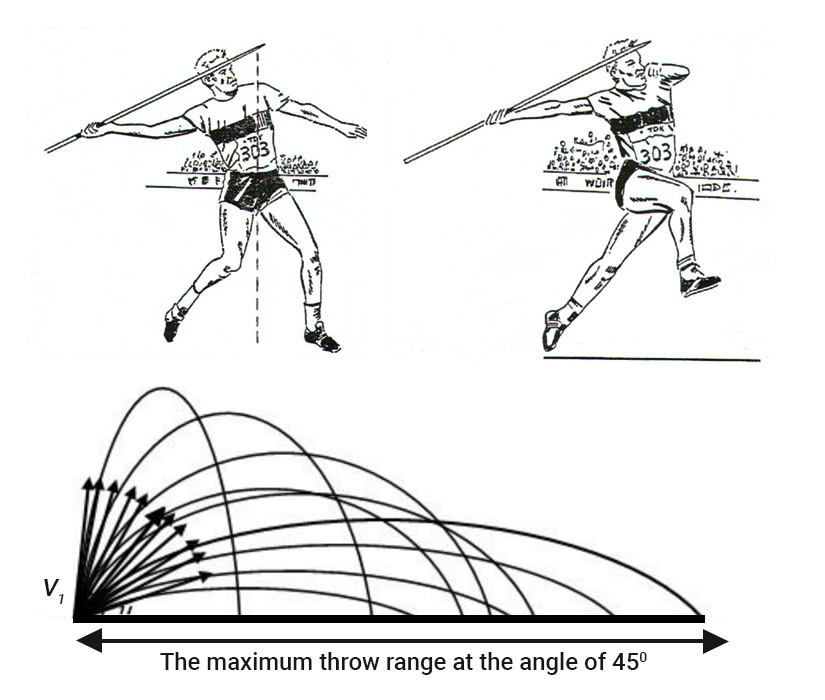
As you can see in the above illustrations with the change in the angle of projection we get different value of horizontal range and it is maximum for angle of projection equal to 45^o

Also Read,

• Class 11 Maths: Cricket, Parabolas And Algebra Walk Into The Field
• The Super Organ: Human Brain Anatomy, Function
• The Real Impact Of Getting Immersed In The Virtual World
• 5 Apps To Help You Avoid Distractions, Become More Productive

Angle Of Projection, Horizontal Range Of Projectile

As the diagram above shows, the maximum horizontal range a javelin can travel depends on the angle of projection, apart from the power delivered by an athlete. it is maximum at 45⁰ in the absence of air resistance and may differ slightly in presence of air resistance and wind. In a sporting event like the Tokyo Olympics 2020, the situation would not have been ideal and there would have been air resistance. But to gain a basic understanding of the physics behind a javelin throw — indeed all projectile motion — let’s assume there was none. The throw that fetched us the gold medal was made between 34 and 36 degrees to the horizontal ground. Some of the other participants threw at higher angles and for that reason, their javelins covered less horizontal range even if they were stronger or held previous records, covering over 90 meters.

Physics: Projectile motion

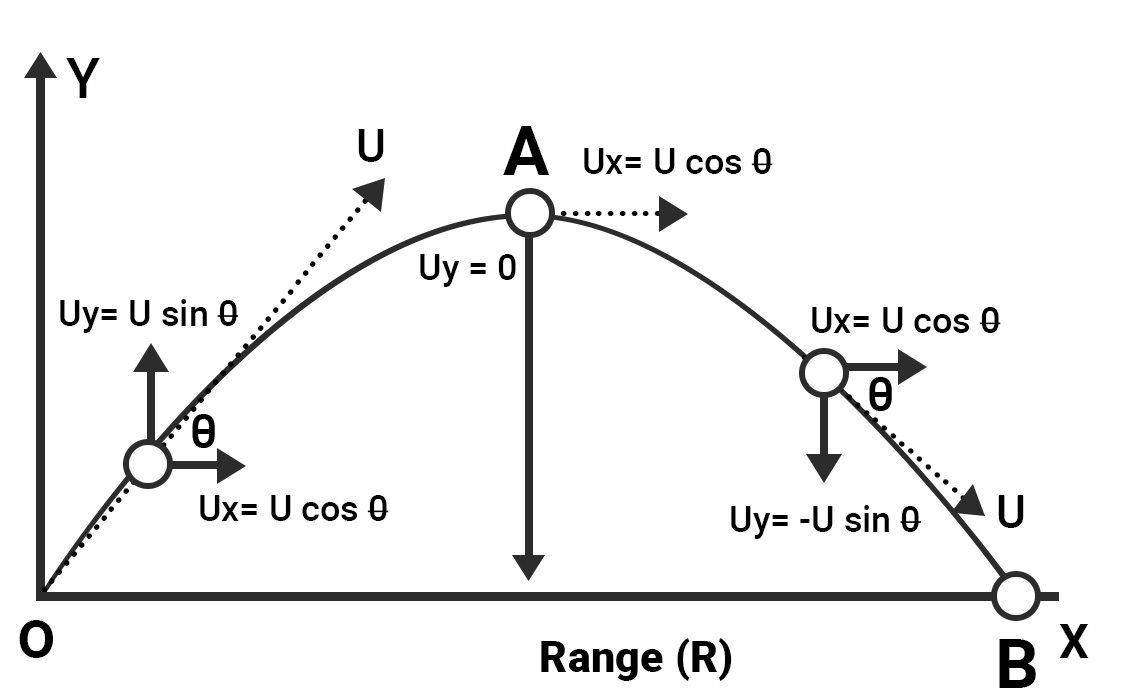
u- speed of projection

g- acceleration due to gravity

θ - Angle of projection

Here taking O at the origin, x and y coordinates of the trajectory of a projectile gives us the information regarding displacement along the X and Y axis respectively

Principle Of Physical Independence Of Motions

• The motion of a projectile is a two-dimensional motion.

• It is difficult to study motion in two dimension but it becomes easier when it resolved into two rectangular components and studied separately.

• As per the principle of physical independence of motions, two mutually perpendicular components are independent of each other.

• Horizontal motion and vertical motion being perpendicular to each other their motions take place independent of each other

• The parameters of the motion of the particle like velocity, acceleration, displacement can be resolved into two mutually perpendicular components — horizontal and vertical

• The horizontal component of velocity remains unchanged throughout the flight. The force of gravity continuously affects the vertical component.

• The horizontal motion is a uniform motion and the vertical motion is a uniformly accelerated motion

Motion along horizontal

Using kinematic equation

$\begin{aligned} & s=u t+\frac{1}{2} a t^2 s=u t+\frac{1}{2} a t^2 \\ & x=(u \cos \theta) t+\left(a_x\right) t\end{aligned}$

As there is no acceleration along the horizontal,

$
\begin{aligned}
& a_x=0 \\
& x=(u \cos \theta) t ----- (1)
\end{aligned}
$

Motion along vertical

$
y=(u \sin \theta) t+\frac{1}{2}(-g) t^2 --- (2)
$

Time taken by projectile to travel from point O to B is Time of flight (T)

For motion between O to B, displacement along Y-axis is y=0 and the time taken here is equal to the time of flight(T)

$\begin{aligned} & 0=(u \sin \theta) T-\frac{1}{2} g T^2 \\ & T=\frac{2 u \sin \theta}{g}\end{aligned}$

Horizontal range of projectile

The horizontal range of a projectile is the distance along the horizontal plane it would travel, before reaching the same vertical position it started from

OR

The horizontal distance travelled by the projectile during a time interval is equal to the time of flight. This is how it is calculated:

$R=x=u \cos \theta(T)=\frac{2 u^2 \sin \theta \cos \theta}{g}=\frac{u^2 \sin 2 \theta}{g}$

Horizontal range

$
R=\frac{u^2 \sin 2 \theta}{g}
$

at

$
\theta=45, \quad R=R_{\max }=\frac{u^2 \sin (2 \times 45)}{g}=\frac{u^2}{g}
$
An angle of projection around 45 degrees may have given us an even better horizontal range.

Speed Of Projection And Rhythm

According to Bartoneitz, “Neeraj was the fastest on the runway. He has to gain energy and then put that energy into the javelin. When you are slow it is hard to do that.” Momentum delivered to that javelin and hence, the speed of projection was better in Neeraj’s case r compared to other athletes. Because of this, he could utilise his power more efficiently.

Let’s find out the speed of projection of a javelin using the horizontal range formula

$\begin{aligned} & R=\frac{u^2 \sin 2 \theta}{g} \\ & R=87.58 \mathrm{~m}=\frac{u^2 \sin (2 \times 35)}{9.8} \\ & u^2=\frac{87.58 \times 9.8}{\sin (70)}=913.3667 \\ & u=\sqrt{913.3667}=30.2219 \mathrm{~m} / \mathrm{s}=108.79 \mathrm{~km} / \mathrm{hr}\end{aligned}$

Neglecting air resistance and the effect of wind speed on the javelin, the speed of projection was an unbelievable 108.79 km/hr or thereabouts. We have seen many modern-day cricket bowlers bowling at or over 150 km/hr but the mass of the cricket ball is just 163 grams. The men’s javelin’s mass is 800 grams. Apart from the power, the correct body posture during the throw to get the best angle of projection and rhythm for effectively transferring momentum to the javelin are a must.