The Mathematics Of Neural Networks And Their Applications In Biology

Neural networks are an exciting field of study that combine mathematics and computer science to mimic the functioning of the human brain. These networks have numerous applications in various fields, including biology. By understanding how neural networks work mathematically, we can better comprehend how they can help us solve complex problems and aid in scientific research.

Neural networks consist of layers of interconnected nodes that are capable of processing and transmitting information. This structure is similar to the way neurons in our brain work together to process information. By using mathematical models, we can simulate the behaviour of these networks and study how they function.

One of the most significant applications of neural networks in biology is in the field of bioinformatics. This field involves analysing large amounts of biological data to identify patterns and relationships. Neural networks can be used to identify patterns in genetic data, predict protein structures, and even help diagnose diseases.

Understanding neurons and their function is not only a crucial aspect of the NCERT Class 10 science curriculum, but it is also essential for competitive exams like the National Eligibility cum Entrance Test (NEET). In this article, try and understand the concept of neurons and neural networks, exploring their fundamental principles, the mathematics involved, and their applications in biology. Our aim is to simplify these complex concepts and present them in an easy-to-understand language that students from Class 10 and Class 12 can comprehend.

Also Read | Mathematical Principles Behind Geographic Information Systems (GIS)

What Are Neurons And Neural Networks?

Neurons are the basic units of the nervous system (as shown below in image) and are responsible for transmitting information throughout the body. They are specialised cells that are capable of generating and transmitting electrical signals, or action potentials, across their membrane.

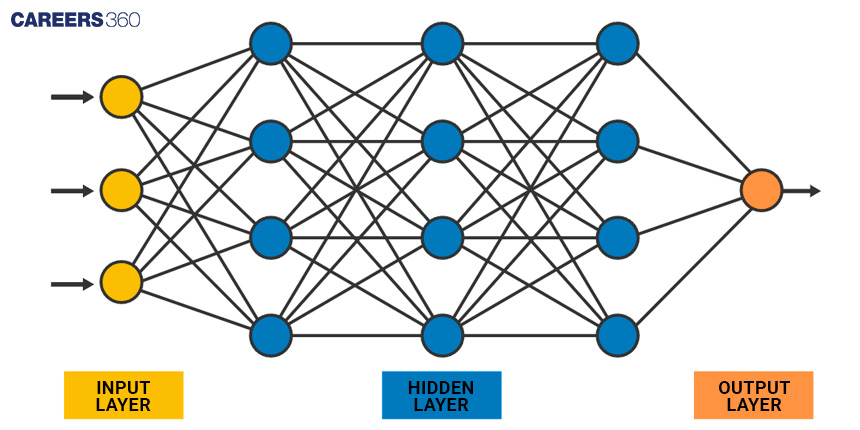
Neural networks, on the other hand, are computational models that are inspired by the structure and function of the human brain. They are composed of interconnected neurons that are organised in layers and are capable of learning from data. In neural networks, each neuron receives input signals, processes them using an activation function, and then passes the output to the next layer of neurons until the final output is produced.

Neural networks are known to be highly effective in solving a wide range of problems, including image and speech recognition, natural language processing, and robotics. They are a fundamental component of modern artificial intelligence and are used extensively in applications such as autonomous vehicles, medical diagnosis, and financial forecasting.

Also Read | Which Concepts Of Physics Are Used While Flying?

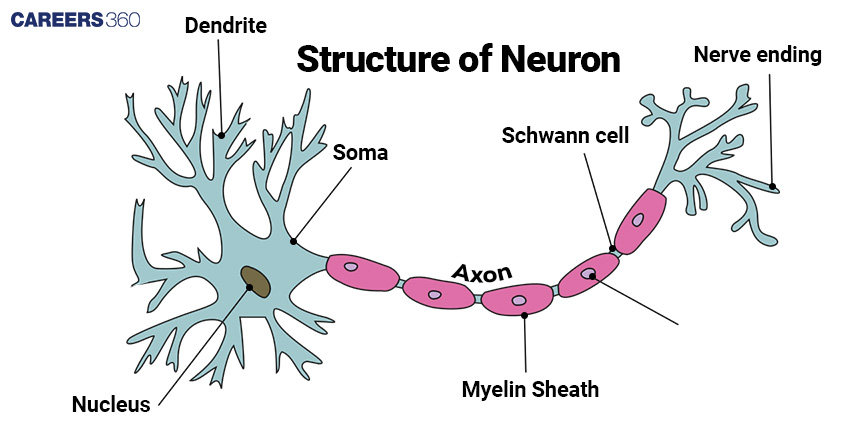
Working Principle Of Neurons

The structure of a neuron consists of three primary components: the dendrites, cell body, and axon. Dendrites are branched structures that extend from the cell body and receive input signals from other neurons or sensory receptors. The cell body or soma processes the incoming signals and integrates them to determine whether or not to generate an action potential. The axon is a long, thin, cylindrical structure that extends from the cell body and transmits electrical impulses to other neurons or effector organs such as muscles or glands.

The electrical impulse or action potential is generated when the input signals from the dendrites and cell body reach a threshold level of depolarization. At this point, voltage-gated ion channels on the axon membrane open, allowing positively charged ions to flow into the cell and initiate the action potential. The action potential then propagates down the axon, jumping from node to node of Ranvier, until it reaches the end of the axon, known as the axon terminal. Refer to the image below for better understanding.

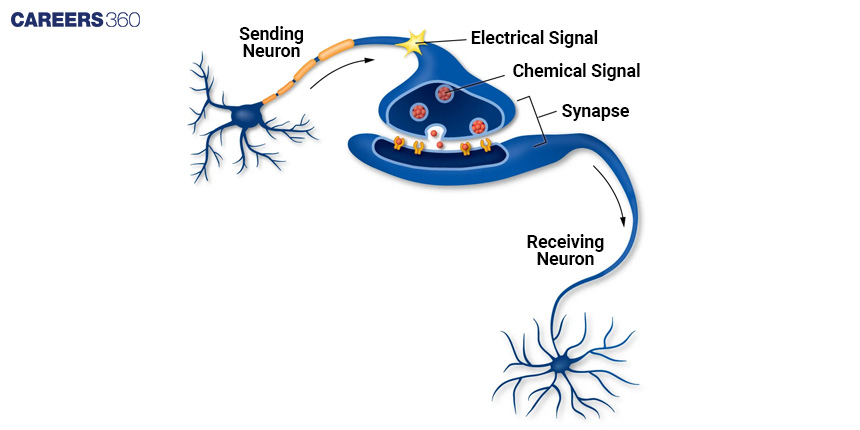
At the axon terminal, the electrical signal is converted into a chemical signal, in the form of neurotransmitters, which are released into the synaptic cleft. These neurotransmitters then bind to receptors on the dendrites or cell body of the receiving neuron, initiating a new round of electrical signals and thus transmitting information throughout the nervous system.

Mathematics Behind The Neural Networks

The mathematics behind neural networks involves a combination of linear algebra, calculus, and probability theory. The basic idea is to model the relationships between input and output data using a set of mathematical functions, which are implemented using interconnected layers of neurons.

A simple example of a neural network is a single-layer perceptron, which consists of a single layer of input neurons and a single output neuron.

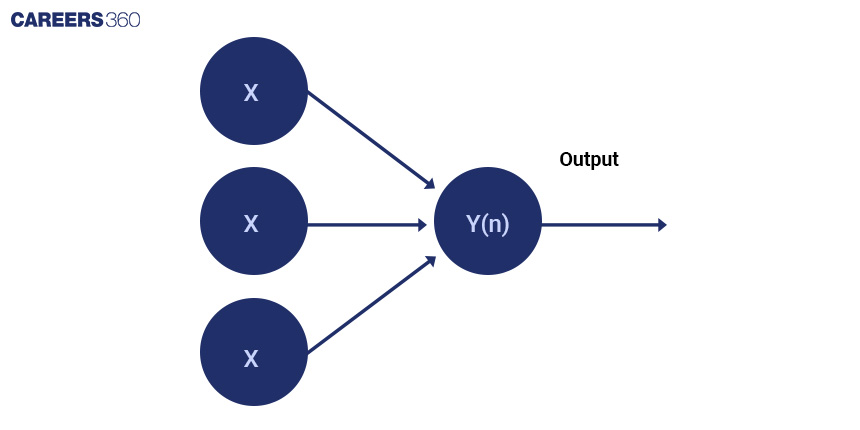
The perceptron can be trained to perform binary classification tasks, such as distinguishing between two categories of data, by adjusting the weights and biases of the neurons based on the input data.

To explain the mathematical concepts involved, let's consider the case of training a perceptron to classify handwritten digits into two categories: even and odd. We can represent each digit as a 28x28 pixel grayscale image, which gives us a total of 784 input neurons (one for each pixel).

The first step in training the perceptron is to randomly initialise the weights and biases of the neurons. We can then feed the input data through the network and compute the output of the single output neuron using a mathematical function called the activation function. One commonly used activation function is the sigmoid function, which maps the input data to a value between 0 and 1.

The output of the perceptron can be compared to the true label of the input data (even or odd) using a loss function, which measures the difference between the predicted output and the true output. One commonly used loss function is the mean squared error (MSE), which computes the average squared difference between the predicted and true outputs.

MSE = 1/n{∑(y_i-Y_i)²}

MSE = mean squared error

n = number of data points

y_i = observed value

Y_i = predicted value

Also Read | How To Recognise And Tackle Food Addiction?

The goal of training the perceptron is to minimise the loss function by adjusting the weights and biases of the neurons. This is done using an optimization algorithm such as gradient descent, which computes the gradient of the loss function with respect to the weights and biases and updates them in the direction of the negative gradient.

For example, if we have a training dataset of 10,000 handwritten digits, we can randomly divide the dataset into training and validation sets (e.g., 80% for training and 20% for validation). We can then train the perceptron on the training set by feeding the input data through the network, computing the output using the activation function, and adjusting the weights and biases using gradient descent to minimise the MSE loss function.

After training, we can evaluate the performance of the perceptron on the validation set by feeding the input data through the network and comparing the predicted output to the true output. We can compute metrics such as accuracy, precision, and recall to assess the performance of the perceptron.

Applications Of Neural Networks In Biology

Neural networks have several applications in biology, including:

1. Brain research: Neural networks are used to model the complex behaviour of the brain and to understand how the brain processes information.

2. Medical diagnosis: Neural networks can be used to analyse medical images and diagnose diseases such as cancer, Alzheimer's, and Parkinson's.

3. Drug discovery: Neural networks can be used to analyse large data sets and identify potential drug targets.