Explore Potential and Kinetic Energy As Experienced On A Garden Swing

Swinging is more than it seems. Whether it's a playground swing or a pendulum, it's all about energy. Let's imagine a child on a swing. When they're at the top, they have lots of energy stored up, called potential energy. As they go down, that potential energy turns into another kind called kinetic energy, which makes them go faster. But how do they keep swinging? It's because energy is always conserved. When they reach the lowest point, their kinetic energy is highest, but the potential energy is lower. Still, they keep swinging back and forth, seeming to defy gravity. It's all about how energy changes and stays the same in a magical dance of swinging.

This Story also Contains

1. Potential Energy
2. Kinetic energy
3. Interplay Between Potential And Kinetic Energy
4. Conservation Of Energy While Swinging

In this article, we will discuss the concepts of potential energy and kinetic energy and how these are involved in this phenomenon.

Potential Energy

Potential energy plays a significant role in the world of swinging. It refers to the stored energy an object possesses based on its position. When it comes to swinging, potential energy comes into play as the object is raised to a certain height or distance from the ground. The higher the object is lifted, the greater its potential energy becomes. This is essential in determining the starting point and height of the swing.

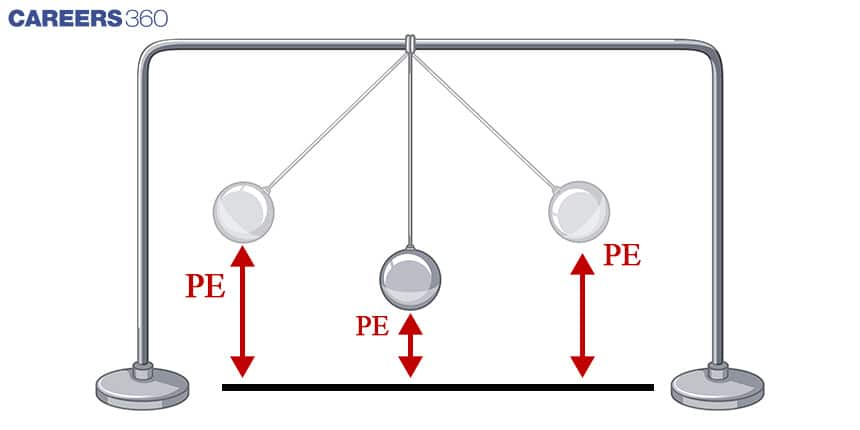
To calculate potential energy in a swinging system, we use the formula PE = mgh where m represents the mass of the object, g is the acceleration due to gravity, and h is the height of the object from the reference point. By plugging in these values, we can calculate the potential energy of the object.

Also Read - Class 12 Biology: Biotech Innovations And Ethical Issues

Kinetic energy

Kinetic energy is a vital component of the swinging phenomenon. It refers to the energy associated with an object in motion. When it comes to swinging, kinetic energy comes into play as the object moves back and forth. It determines the speed and intensity of the swinging motion, adding excitement and thrill to the experience.

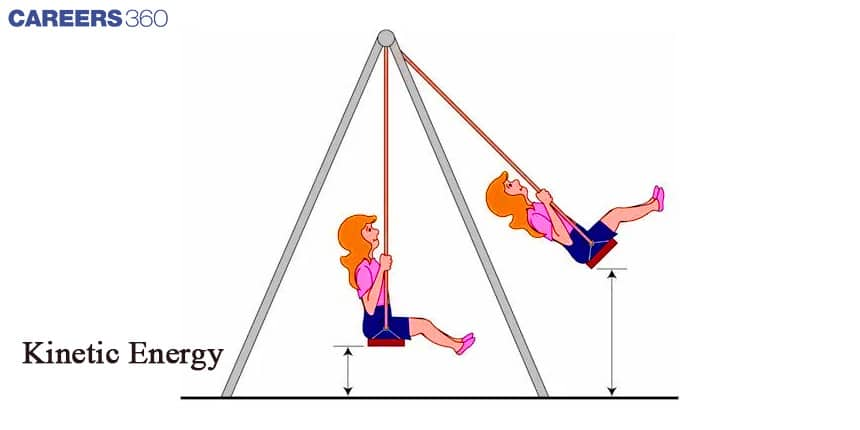
To calculate the kinetic energy in a swinging system, we use the formula

KE = 1/2 mv² where KE represents kinetic energy, m is the mass of the object, and v is its velocity or speed. By plugging in these values, we can find the amount of kinetic energy possessed by the swinging object.

Kinetic energy actually shows up in a variety of swinging situations. For instance, potential energy is converted into kinetic energy, resulting in a thrilling rise in speed as a youngster drops from the highest point of a swing. Similar transitions between potential and kinetic energy occur as a pendulum's bob swings back and forth, with the lowest point of the swing containing the most kinetic energy.

Interplay Between Potential And Kinetic Energy

The swinging motion involves a captivating interplay between potential and kinetic energy. At the highest point of the swing, potential energy is at its maximum, while kinetic energy is minimal. As the swing descends, potential energy gradually converts into kinetic energy, resulting in a thrilling increase in speed. At the lowest point, kinetic energy reaches its peak, while potential energy is minimal. This energy conversion continues as the swing oscillates back and forth, with potential energy transforming into kinetic energy and vice versa.

Understanding the interplay of potential and kinetic energy in swinging provides insights into the dynamic nature of the motion. Visualizing the conversion of energy as the swing rises and falls helps us appreciate the continuous exchange between potential and kinetic energy. It underscores the importance of energy conservation and enhances our understanding of the fundamental principles that govern swinging systems.

Conservation Of Energy While Swinging

During swinging, where energy is neither generated nor destroyed but rather transferred between different forms, the law of conservation of energy is applicable. The total mechanical energy in swinging systems, which is the product of kinetic and potential energy, is constant throughout the motion. Potential energy is transformed into kinetic energy when the swing moves and vice versa, keeping the total mechanical energy in balance. As long as no major external forces, such as friction or air resistance, have an impact on the swing, this conservation is attainable.

But in actual situations, energy losses actually happen as a result of things like friction and air resistance. The total mechanical energy of the swing is progressively decreased over time by these losses, which causes a minor reduction in height and speed. The wasted energy is released as heat or sound.

Pendulums and playground swings are two examples of swinging systems where energy is conserved. The interaction of potential and kinetic energy in both situations guarantees that the overall mechanical energy stays constant, permitting the swinging motion to continue.

Hope you have gained a fresh outlook of how the interaction between kinetic and potential energy influences swing movement. Appreciate the importance of energy conversions in optimizing swinging experiences and learn how these concepts are applied in real-world applications. This newfound knowledge will help you yo recognise the physics behind the playing on a swing, enhancing your overall understanding of this dynamic and joyful activity.

Also Read - Mathematics Of Optics: Understanding Light And Its Interactions With Matter