Learn To Solve Maths Alligation And Mixtures Problems like A Pro

Maths problems can sometimes feel like tricky puzzles, and one set of puzzles that often comes up is all about Alligations and mixtures. Imagine it like finding the right mix for a recipe or figuring out how different things blend together. These problems are not just numbers on paper; they connect what we learn in school to the real world. Whether you're in class or facing challenges outside of school, understanding how to solve these mix-and-match puzzles is super useful.

So, why does this matter, especially for students? Well, these problems pop up a lot in tests and exams. But it's not just about passing a test; it's about learning skills that will help you solve problems in everyday life. Think of it as levelling up your brainpower! This article will guide you through the secrets of solving these mix-and-match puzzles. Whether you love maths or find it a bit tricky, keep reading this article to make solving Alligations and mixtures problems a breeze!

Alligations And Mixtures Related Concepts

>> Ratios and Proportions: Let's consider a scenario where you're blending coffee beans of different qualities to create a custom coffee blend. If you have coffee beans A and B in the ratio 3:2, and you want to make 500 grams of the blend.

In this blend these two type of coffee beans are in ratio of 3:2 means in five equal parts, three parts of coffee A and two parts of coffee B. Using the proportion concept, the quantity of A can be calculated as

35500 grams

= 300 grams.

And quantity of coffee B

25500 grams

= 200 grams.

>> Percentages: Imagine you have a cleaning solution that is 20% bleach. If you want to make 1 litre of a solution with 10% bleach.

20% bleach solution means

Pure bleach quantity = 201001000=200 grams in 1000 ml

10% bleach solution means

Pure bleach quantity = 101001000=100 grams in 1000 ml

The amount of 20% bleach needed = 1002001000 = 500 ml

To make a 10% bleach solution take 500 ml of the original 20% solution and add 500 ml of water.

>> Equations and Variables: Suppose you have a mixture of nuts and raisins, and the total weight is 2 kilograms. If the weight of nuts (x) is half the weight of raisins, the equation becomes x + 2x = 2000 grams.

Solving for x, you get x = 666.67 grams, and 2x (raisins) is 1333.33 grams.

>> Weighted Averages: Consider a financial portfolio with two investments, one with a 5% return and the other with a 10% return. If you have ₹50000 invested in the 5% and ₹30000 in the 10%, the weighted average return is calculated as

((0.05 * 50000) + (0.1 * 30000))50000 + 30000100=6.875%

Also, check - Tardigrades: Nature's Indestructible Microscopic Creatures

Trick To Solve Alligation And Mixtures Problems

If you have two things, one cheaper and one more expensive, and you want to find out how much of each to mix to get something in the middle, there's a simple way.

Formula Method:

You compare the quantity of the cheaper thing to the quantity of the more expensive one using a formula. It looks like this:

Quantity of cheaperQuantity of dearer=Price of dearer – Mean priceMean Price – Price of cheaper

Diagram Method:

But, if you prefer a simpler way, you can use a diagram to understand it better. It's easier to visualise.

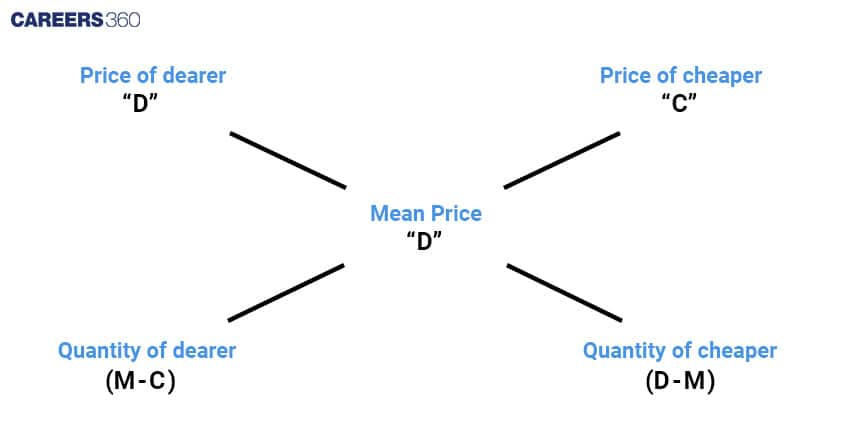Alligation is like a helper that lets you figure out the average price when you mix two or more things. It also helps find the right mix to get a specific price or concentration.

The formula (M−C)(D−M) is just a way to find the ratio of the quantities of both things. So, if you already know the ratio, you can find the average (mean) easily.

Now, let's practise solving some problems with this method. It'll make the concept clearer and more fun!

Problem 1: A tricky shopkeeper decides to mix cheap rice that costs Rs. 10 per kilogram with good-quality rice priced at Rs. 25 per kilogram. After mixing them, he sells the combination for Rs. 15 per kilogram. Can you figure out the ratio in which he mixes the two types of rice?

Solution:

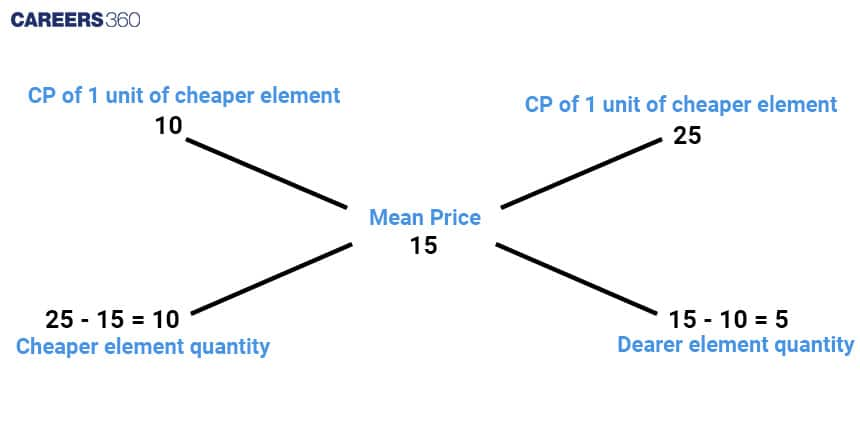
So, the amount of the cheaper rice to the good quality rice is like 10 to 5, which simplifies to 2 to 1.

Problem 2: Imagine you have two glasses. One is filled up to about one-third, and the other is filled up to about one-fourth with milk. Now, let's top them both up with water and mix everything in a big pot. What do you think the mix of milk and water will be? What's the ratio of milk to water in the pot now?

Solution:

Two equal glasses.

Glass 1: 1/3 full of milk.

Glass 2: 1/4 full of milk.

Both glasses are then filled up, resulting in total volumes of 2/3 and 3/4 water in Glass 1 and Glass 2, respectively.

Step 1: Initial Quantities of Milk:

Glass 1: 1/3 milk.

Glass 2: 1/4 milk.

Step 2: Total Volume After Filling with Water:

Glass 1: 1 - 1/3 = 2/3 water.

Glass 2: 1 - 1/4 = 3/4 water.

Step 3: Contents in the Pot:

Glass 1 in the pot: 1/3 milk, 2/3 water.

Glass 2 in the pot: 1/4 milk, 3/4 water.

Step 4: Overall Ratio in the Pot:

Total Milk: 1/3 + 1/4 = 7/12.

Total Water: 2/3 + 3/4 = 17/12.

Step 5: Simplified Ratio:

Final Ratio: 7/12 : 17/12.

So, the ratio of milk to water in the pot is 7:17.

Problem 3: There's a bottle with 20 litres of liquid A. We take out 4 litres of A and put in 4 litres of liquid B. Then, we do it again. What's the ratio of the remaining liquid A to the liquid B in the bottle now?

Solution:

The bottle had 20 litres of liquid A.

Step 1: We took out 4 litres of liquid A and put in 4 litres of liquid B.

Liquid A left in the bottle: 16 litres.

Now, the mix is 4/5 liquid A and 1/5 liquid B.

Step 2: Again, we took out 4 litres of the mix.

In that 4 litres, there were 16/5 litres of liquid A and 4/5 litres of liquid B.

So, in the bottle, we have 64/5 litres of liquid A and 16/5 litres of liquid B.

Step 3: Now, we added 4 litres of liquid B.

The total amount in the bottle becomes 20 litres.

In this mix, there are 64/5 litres of liquid A and 36/5 litres of liquid B.

The ratio of liquid A to liquid B is 16 to 9.

So, in simpler terms, after all these steps, there's more liquid A than liquid B, and the ratio is 16 to 9.

Also, check - Does Lower Voltage Mean You’re Saving Electricity?

Hope this helps you better understand concepts such as Alligations, mixtures, ratios, proportions, weighted averages, and how to tackle problems connected to these ideas.