Calculus Of Half Life: Radioactive Decay And Mathematics

The phenomenon of radioactive decay, a natural process in which unstable atomic nuclei disintegrate and release radiation, has fascinated scientists for over a century. Understanding the rate at which radioactive substances decay is crucial in various fields, including nuclear physics, radiology, archaeology, and medicine. To delve into the mathematics behind this intriguing process, we explore the calculus of half-life, which provides a mathematical framework to model and quantify radioactive decay.

The Physics NCERT Chapter 13 Nuclei covers topics such as nuclear stability, radioactive decay, types of radioactive emissions, decay laws, and half-life calculations. The questions related to half-life, decay constant, and decay equations are being asked in competitive exams such as NEET, JEE, CBSE, and board exams. These concepts are also used in the fields of medicine, engineering, and fundamental scientific understanding. A strong grasp of these concepts not only contributes to scoring well in these exams but also lays a solid foundation for further studies in scientific and technical disciplines.

Concept Of Half Life

The half-life of a radioactive substance is defined as the time it takes for half of the initial quantity of radioactive nuclei to decay as shown below in the graph. It is denoted by "t½" the half-life is a characteristic property of each radioactive material and can vary widely depending on the specific isotope.

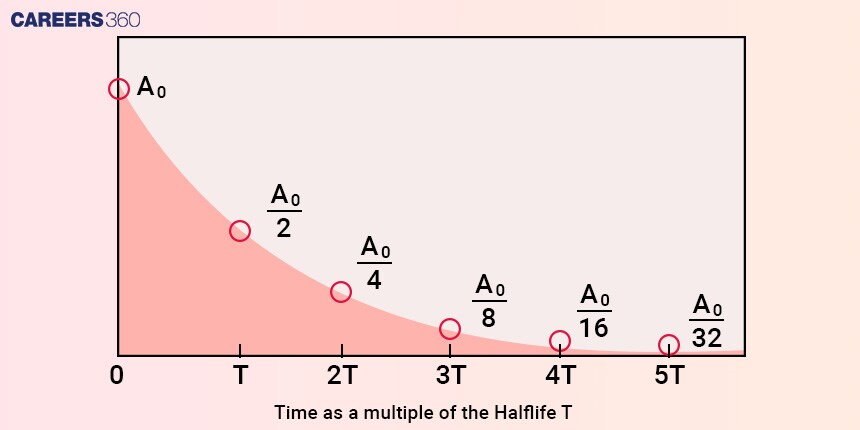
Where A0 is the original amount of radioactive substance and T is half life.

Also check - Understanding Maxwell's Equations: A Mathematical Perspective

Differential Equations And Radioactive Decay

Calculus plays a fundamental role in modelling radioactive decay. By formulating the decay process as a first-order linear ordinary differential equation, we can mathematically describe the rate of change of the number of radioactive nuclei over time. The differential equation is given as:

dN/dt = -λN

Here, dN/dt represents the rate of change of the number of radioactive nuclei with respect to time, N represents the number of radioactive nuclei at time t, and λ is the decay constant. The negative sign indicates that the number of radioactive nuclei decreases over time.

Solving The Differential Equation

To find the number of radioactive nuclei as a function of time, we solve the differential equation using integration.

In this equation, N(t) represents the number of radioactive nuclei at time t, N₀ represents the initial quantity of radioactive nuclei, and e represents the base of the natural logarithm. As time progresses, the exponential term decays, leading to a reduction in the number of radioactive nuclei.

Half Life Formula

The half-life formula is derived from the decay constant. It relates the half-life (t_½) of a substance to its decay constant (λ) through the equation:

We know the decay equation.

N(t) = N₀e^-λt

The time in which half radioactive substance is decayed

This means N(t) = N₀ /2

Putting the N(t) value in the decay equation.

N₀ /2 = N₀e^-λt

1/2 = e^-λt

Taking natural log both sides

-ln 2 = -λt_1/2

t_1/2 = (ln 2)/λ = 0.693/λ

This formula provides a direct relationship between the half-life and the decay constant, allowing us to calculate one from the other. It demonstrates that the half-life is inversely proportional to the decay constant.

Mean Life Formula

The decay equation is given as N(t) = N₀e^-λt

For average or mean life of radioactive decay

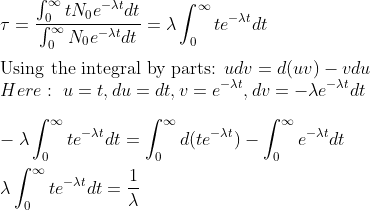
Therefore,

Average life or mean of radioactive decay is given by

τ = 1/λ

t_1/2 = 0.693/λ = 0.693 * τ

Applications And Examples

The calculus of half-life finds practical applications in numerous scientific disciplines. In nuclear physics, it helps in determining decay rates and understanding the behaviour of radioactive substances. In radiology, the half-life concept is used to calculate the appropriate dosage and timing for medical imaging procedures. Archaeologists employ half-life calculations to estimate the ages of ancient artefacts or organic remains. Additionally, in nuclear medicine, the concept of half-life is utilised to ensure the safe administration of radiopharmaceuticals to patients.

Solved Problems

To illustrate the practical use of the half-life formula, let's consider some examples. Suppose we have a radioactive substance with a decay constant of 0.05 per year. Calculate the time in which the initial quantity of the substance decays half.

Solution:

We know half life formula

t_1/2 = ln 2/ λ = 0.693/λ

t_1/2 = ln 2/(0.05) = 0.693/0.05 = 13.86 years

This calculation indicates that it takes approximately 13.86 years for half of the initial quantity of the substance to decay.

Problem: (CBSE 2020)

(a) Derive the law of radioactive decay N(t) = N₀e^-λt

(b) The half life of undergoing α decay is 4.5*10⁹ years. Find its mean life.

Solution:

Derivation of N(t) = N₀e^-λt is discussed above in this article.

Given that t_1/2 = 4.5 x 10⁹

We have discussed the mean life formula.

t_1/2 = 0.693/λ = 0.693 * τ

τ = (4.5*10⁹)/0.693

= 6.49*10⁹ years

Also check - How Much Of AI Is Inspired By Biological Neural Networks?

Hope, you should have gained a comprehensive understanding of radioactive decay, half-life, mean life, and the mathematical principles underlying these concepts.