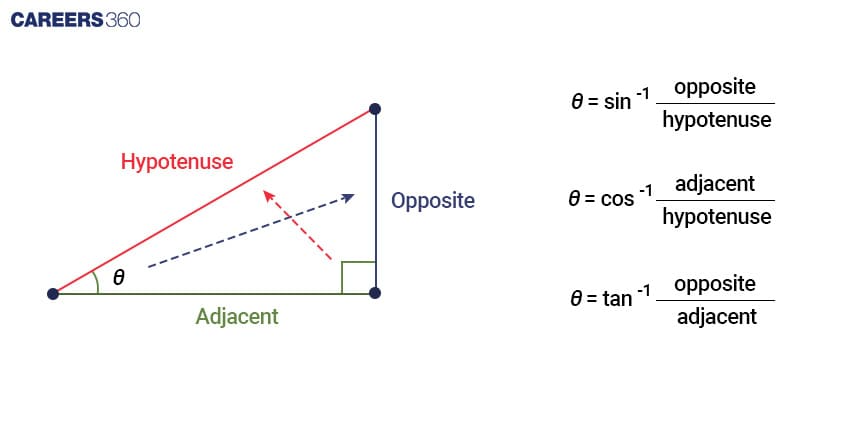
Trigonometry: Where Do We See It Being Used In Real-Life?

How does a basketball player precisely calculate the angle to score a basket, or how do archers consistently hit a bullseye? Or how is the camera set to an exact angle to capture the maximum view or configuring medical devices like CT scans and X-rays to reveal intricate bone fractures or organ injuries?

All of this is possible thanks to Trigonometry and Inverse Trigonometry, where angels aren't just numbers but keys unlocking precision across countless real-life scenarios. From sports to engineering, photography to medicine, the concept of inverse trigonometry silently underpins countless practical applications we encounter daily.

In the NCERT syllabus for Class 12, inverse trigonometry holds significant importance. Understanding inverse trigonometric functions like arcsine, arccosine, and arctangent is crucial for solving complex problems involving angles and side lengths in triangles. These concepts not only form an integral part of the Class 12 board exams but are also fundamental in various competitive exams like JEE, NEET, and other entrance tests. Mastering inverse trigonometry opens doors to higher studies in mathematics, physics, engineering, and other fields where advanced mathematical problem-solving skills are required. Proficiency in these concepts is essential as they serve as building blocks for topics in calculus, differential equations, and further mathematical studies at the undergraduate level and beyond.

What Is Inverse Trigonometry?

Inverse trigonometry is like a secret code that helps find angles when we know certain ratios or lengths in shapes like triangles. Imagine you have a mystery angle and know some sides of a triangle. Inverse trigonometry helps crack this mystery and tells the angle using these known sides or ratios.

Artillery And Projectile Motion

Military and ballistics use inverse trigonometry to calculate launch angles for projectiles.

In battles and shooting, like when cannons or missiles are fired, getting the right launch angle greatly matters. Figuring out this angle is where inverse trigonometry jumps in. It helps experts decide how to aim these projectiles accurately.

Imagine a cannon aiming 5,000 metres away with a starting speed of 300 metres per second. By using inverse trigonometry, we can find the right launch angle (let's call it θ).

The horizontal distance travelled (x) can be related to the initial velocity (v) and launch angle (θ) using the equation:

x = V²sin2θ/g

= (1/2){sin^-1(xg/v²)}

= (1/2){sin^-1(5000*9.8/300²)}

= (1/2){sin^-1(0.544)

= 32.97 Degree

Therefore, the cannon should be set to an angle of 32.97 degrees with a speed of 300m/s to hit an object 5,000 m away.

A basketball player is standing six metres away from the hoop. If they want to make a direct shot into the hoop and the hoop is three metres high, at what angle should the player aim the ball?

Distance (x) = 6 metres

Height of hoop (h) = 3 metres

We'll use the tangent function to find the angle. The tangent of an angle in a right-angled triangle is the ratio of the opposite side to the adjacent side.

tan(θ)= h/x

Where

θ = Angle of elevation

tan(θ)= 3/6 = 0.5

θ = tan^-1(0.5) = 26.56 degrees.

Therefore, the player should aim the ball at an angle of 26.56 degrees to shoot directly into the hoop.

Medical Imaging

In medical imaging like MRI or CT scans, angles of radiation beams are computed using inverse trigonometry to precisely target affected areas.

A CT scan aims to capture an image of a bone fracture located eight centimetres deep within a limb. If the X-ray source is positioned 12 centimetres away from the fracture site, what angle should the radiation beam be directed at?

Distance from the X-ray source to the fracture (x) = 12 centimetres

Depth of the fracture (d) = 8 centimetres

tan(θ) = 8/12 = 0.667.

θ = tan^-1(0.667) = 33.70 degrees.

Therefore CT scan aims to capture the fracture at an angle of 33.70 degrees.

Also check - Genetics And Human Health: Decoding The Genetic Code For Medical Insights

Optics And Camera Angles

In photography and optics, understanding angles of view and lens positioning involves inverse trigonometry for capturing precise images and adjusting focus.

A CCTV camera is mounted at a height of six metres and is required to cover a viewing area 10 metres away. What angle should the camera be inclined at to cover the maximum area?

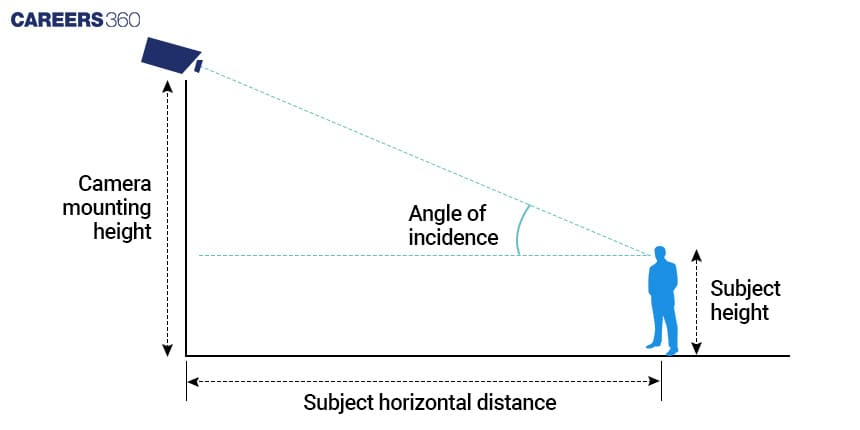
Height of CCTV camera from the ground (h) = 6 metres

Distance to the edge of the viewing area (d) = 10 metres

We'll use the inverse tangent function to find the angle of inclination:

Tan(θ) = 6/10 = 0.6.

θ = tan^-1(0.6) = 30.96 degrees.

Therefore CCTV cameras should be at an angle of 30.96 degrees.

Determining Heights Using Shadows

In architecture, inverse trigonometry aids in finding heights. Suppose an architect assesses the height of a building. At noon, he measures the shadow cast by the building to be 15 metres long. Given that the angle of elevation from the tip of the shadow to the top of the building is 60 degrees. Determine the height of the building.

tan ? = height/base

tan 60 = height/15

Height = 15 tan 60

Height = 153

Hence the height of the building is 153 m.

Astronomy and Stargazing

In astronomy, angles to celestial objects are determined using inverse trigonometry. If an observer knows the distance to a star and the angle subtended by it, they can calculate the star's actual position.

Suppose an astronomer is observing a star from Earth. Given that the star is at a distance of 10 light-years away, and the angle subtended by the star from Earth is 0.1 degrees. find the actual size of the star.

The relationship between the distance to an object, the actual size of the object, and the angle it subtends can be represented as:

Distance = Actual Size / tan?

Also 1 light-years = 9.46*10¹² kilometres

Actual Size = distance * tan?

Actual Size = 10 light years * tan(0.1)

Actual Size = 10*9.46*10¹²(0.0017)

Actual Size = 165.10*10⁹ kilometres.

Therefore, based on the observed angle and known distance, the approximate actual size of the star is 165.10*109 kilometres.

Also check - Understanding The Concepts Of Economics Through Real-Life Examples

Hope now you will understand the importance of inverse trigonometry, and how it is used in our daily life from sports to engineering, from photography to medicine.