Class 12 Maths - 10 Most Likely Questions You Must Prepare

Four topics from the Class 12 Mathematics syllabus for the Central Board of Secondary Education (CBSE) together account for close to 80% of all questions asked in the board exam. These four topics are Calculus, Vector and Three- Dimensional Geometry, Algebra and Probability.

Questions based on certain concepts have been asked repeatedly through the years. Once all concepts are clearly understood, it is a good idea to direct attention specifically to topics that are tested on most often.

Given below are the most important sections along with a few most commonly-asked questions along with solutions.

Calculus

This unit includes five topics which are correlated to each other. If you have grasped the fundamental concepts of integration, continuity and differentiability, then you can score high marks in the other three topics of this unit because these are nothing but the application of integrals and derivatives.

New: Meet Careers360 B.tech/NEET Experts in your City | Book Your Seat now

Latest: Download CBSE Syllabus 2025-26 for Class 9, 10, 11, 12th

Don't Miss: 50+ Entrance Exams: 10+2 Students Must Not Miss

Top UGC Approved Colleges Offering: Online B.Sc | Online BA | Online BBA | Online BCA

Integration

This is the reverse process of differentiation and it is used for adding or summing up the parts to find the whole. There are two types of integrals,

Definite Integrals: If an integral contains a lower and upper limit then it is a definite integral. It is represented as,

_a∫^b f(x) dx

Indefinite Integrals: If an integral does not have a lower or upper limit then it is an indefinite integral. It is represented as,

∫ f(x) dx = F(x) + C , where C is constant.

There are some methods for finding integrals,

• Integration by substitution.

• Integration by parts.

• Integration using by partial fraction

Here are some often-asked questions..

Q.1 : Evaluate following integrals:

1. ∫ 5bx(a+2x) dx

2. ∫ 7bx/ ( c² + a² x² ) dx

3. ∫{( sin²x - cos²x)/ (sinx.cosx)} dx

4. ₁∫³ ( 5x² + 3x) dx

5. _-1∫¹ ( 7x³+ 3x + 11) dx

Q.2 :

(1). Evaluate given functions using the substitution method:

1. ∫ { (sec²x ⋅ sec²x )/(tan²x)}dx

2. ∫ (cos³x ⋅ sin²x )dx

(2).

1. Find the area of region lying above the x-axis and bounded by the circle x² + y² - 12x = 0 and inside the parabola y² = 4x.

2. Find the area of the region bounded by y² = 12x , x =3 , x =5 and above the x-axis.

3. Find the area of the curve y = sin2x between 0 to 2π.

Another fundamental topic is Differentiation. It measures the instantaneous rate of change of any function with respect to its variables. Differential equations and continuity and differentiability are the applications of differential and integrals. For example, velocity is the rate of change of displacement with respect to time. If x and y are two variables then the rate of change of x with respect to y is given by dy/dx. It is also represented by f’(x).

Here are some questions from that section.

Q.1 :

a. Find the order and degree of given equations:

1. x³ (d²y/dx²) = {1 + (dy/dx)²}³

2. x⁴ (d²y/dx²)³ + (dy/dx)³ = 0

3. d²y/dx² + x(dy/dx)³ = 5x² log(d²y/dx²)

b. Determine the point of discontinuity of given functions:

1. f(x) = (x+2)/{(x-3)(x+5)}

2. f(x) = (x²+ 5x + 6)/(x² + 2x - 3)

Q.2 :

a. Find the differential equations representing the family of following curves:

1. y = 5q cos( x + p ), p and q are constant.

2. A circle having a centre on the x-axis and radius 5 unit.

b. Find the general solution of differential equations which are given below:

1. y² dx = x² dy

2. dx/dy = (1 + x²)/(1 + y²)

3. dx/dy = 1 + x +y + xy , at x= 1 and y =0

Q.3 :

1. In a city, the Covid-19 virus initially infected 5,000 citizens. Numbers have increased by 5 % in 2 days. In how many days will the count reach 30,000, if the rate of growth of virus is proportional to the number present?

2. Show that every polynomial function is a continuous function.

3. Find the equation of a curve which is passing through point ( 1, 3) and slope of the tangent at any point (x, y) is x ²/ 2xy .

Vector And Three-Dimensional Geometry

A quantity that has magnitude as well as direction is a vector. A scalar quantity has only magnitude.

Some important concepts are described below.

Position Vector

It is given with respect to the origin O (0,0,0), where the coordinates of point A are x, y, and z.

Magnitude of vector = | OA | = √(x² +y²+z²)

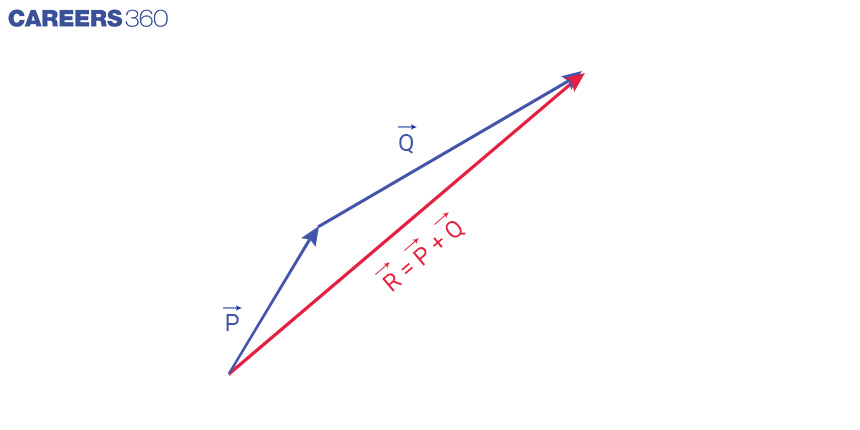
• Sum of two vectors,

R = P + Q

Product Of Vectors

There are two types of product

1. Scalar product (Dot product) : If P and Q are two vectors then

P ⋅ Q = |P |⋅|Q|cos(θ) , where θ is the angle between P and Q .

2. Vector product (Cross product):

Let P = ai +bj+ ck and Q =xi +yj+ zk

P × Q = (bz - cy)i + (cx - az)j+ (ay - bx)k

Magnitude of cross product

|P × Q| = |P |⋅|Q|sin(θ) , where θ is the angle between P and Q .

• Vector equation of a line that passes through a vector a and parallel to the vector b is

r = a + λb

• The position vector of a point R dividing a line segment joining the points P and Q whose position vectors a and b respectively in the ratio m: n is given by:

(i) Internal dividation = (na + mb) / (m + n)

(ii) External dividation = (na - mb) /( m - n )

• The distance between parallel lines r = a1 + λb1 and r = a2 + μ b2

|(b1⨯b2).( a2 - a1) | / |(b1⨯b2)|

• The Direction cosines of a line joining two points P (x1, y1, z1) and

Q (x2, y2, z2 ) are,

L = (x2- x1) / PQ, m= (y2 - y1) / PQ , n= (z2- z1) / PQ

Where, PQ = √{(x2-x1)²+(y2-y1)²+(z2-z1)²}

If l, m, and n are the direction cosines of a line, then l² + m² + n² = 1.

• Equation of a line which is passing through a point (x1 , y1 , z1 ), having direction cosines l, m, n is:

(x - x1) / l = (y - y1) / m = (z - z1) / n

• Equation of a plane which is passing through a given point (x1 , y1 , z1 ) and perpendicular to a given line with direction ratios P, Q, R and is,

P (x - x1) + Q (y - y1)+ R (z - z1)= 0

• Cartesian equation of a line which is passing through two points (x1,y1,z1) and (x2,y2,z2) is,

(x-x1)/(x2 - x1) = (y-y1)/(y2 - y1) = (z-z1)/(z2 - z1)

Some important questions are given below

Q.1 : Find the solution of given questions:

a. Find the cross product and dot products of given vectors

1. P = 2i + 3j+4k and Q = i - 2j+3k

2. P = i - 5j+2k and Q = 3i - 2j+2k

b. Find the unit vector of given vector P and Q in the direction of sum of vector P and Q .

1. P = 1i + 2j-4k and Q = 2i - 3j+3k

2. P = 2i - 3j+2k and Q = 3i - 2j+3k

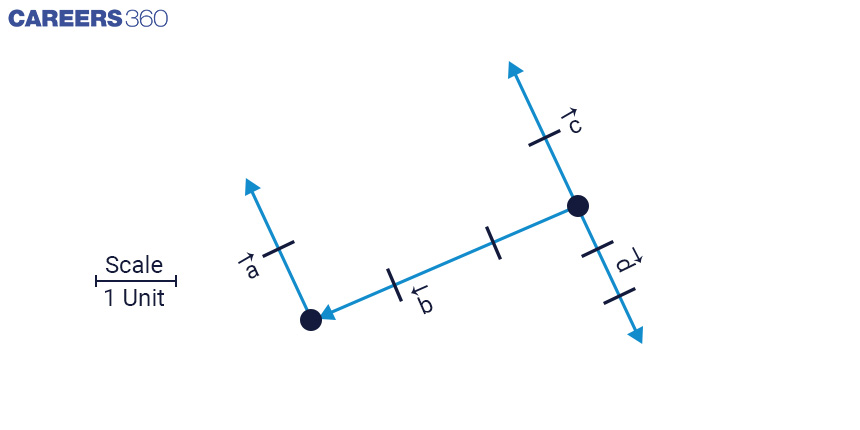
c. Identify the linear, equal, and co-initial vectors in the given figure

Q. 2: Solve the following questions

1. Find the value of x if the vectors P = 3i + xj+k and Q = 9i - j+3k are parallel.

2. Find the value of angle between P = 3i + 2j+k and Q = 1i -2 j+3k

3. Find the area of triangle ABC with vertices A( 2,2,4), B( 2,5,3), C( 3, 1, 2).

4. Find the area of parallelogram whose diagonals are represented by vectors 4i -6 j+8k and 4i - 2j+4k .

5. If P = i + 2j-3k and Q = 3i - j+2k are two vectors then show that (P + Q ) and (P - Q ) are perpendicular to each other.

6. Show that (p - q)×(p + q) = 2(p × q).

Q.3: Solve following questions

1. Find the equation of line which is passing through the point A ( 1, 4, 5) and parallel to the vector 3i + 2j+k .

2. If a line makes angles 45^º , 60^º and 90^º with the x, y and z-axis respectively, find its direction cosines.

3. If a line makes angles 90^º , 60^º and θ with x, y, and z-axis respectively, where θ is an acute angle then find the value of θ .

4. Find the cartesian equation of line which passes through the point ( -4, 8 , -10 ) and is parallel to the line (x+3)/6 = (4-y)/10 = (z+8)/12 .

Algebra

This unit includes matrices and determinants. These have various applications in science, engineering, economics and other fields. Some important properties and concepts are given below.

• If two columns or rows are interchanged then the sign of determinant changes

• If the rows and columns of a determinant are interchanged then the value of the determinant will be unchanged.

• Value of a determinant will be zero (0), if two identical rows or columns are present in the given determinant.

• If each element of a column or row is multiplied by constant k then the value of the determinant obtained is multiplied with k.

• A square matrix A = [a_ij] is said to be symmetric if the transpose of A is equal to A, that is, [a_ij] = [a_ji] for all possible values of i and j.

• A square matrix A = [a_ij] is said to be a skew-symmetric matrix if A’ = -A, that is a_ij=-a_ij for all possible values of i and j.

• For a skew-symmetric, if we substitute i=j, we have a_ii=-a_ii and thus 2a_ii = 0 or a_ii=0 for all i. There, all the diagonal elements of a skew-symmetric matrix are zero.

• Suppose A and B are two matrices with the same order m, such that AB = BA = I, then B is called the inverse matrix of A, and it is denoted by A^-1. and A is known as invertible matrix.

Also check - CBSE Class 12 Biology: 10 Most Asked Questions On Genetics And Evolution In Boards

Some important questions are given below.

Q.1: Estimate the following

1. If 2A - B = 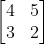And B = 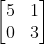Find the value of matrix A,

2. If A is the Square matrix such that A2 = I then find the value of ( A + I )2 + ( A -I )2 + 5A .

3. Find the value of ( a + b) if

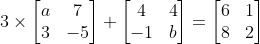
4. Find the value of x if

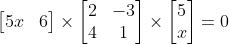
5. Simplify

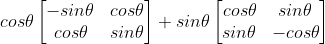
Q.2:

1. Show that

2. det 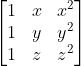= ( x - y )( y - z )( z - a )

2. det 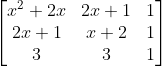= ( x -1 )³

b.using properties of determinant

1. Find the value of det

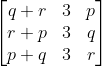
2. Find the value of f(2) - f’(1) if

f(x) = det 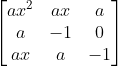, where a = 5

Probability

There are many applications of probability in real life. Every CBSE Class 12 board exam Maths paper has included questions related to dice, coins, playing cards and real life situations. There are several important concepts and formulas in probability theory that are used to calculate the likelihood of different events occurring. Some of the most important ones include:

• The probability of an event occurring is given by the formula:

P(A) = n(A) / n(S),

Where, P(A) is the probability of the event,

n(A) is the number of favourable events that occur,

n(S) is the total number of possible outcomes.

• The probability of two independent events:

P(A ∩ B) = P(A) * P(B),

Where P(A) and P(B) are the probabilities of both events occurring.

• The probability of an event occurring given that another event has already occurred is called conditional probability and is given by the formula:

P(A | B) = P(A ∩ B) / P(B),

Where, P(A ∩ B) is the probability of both events occurring

P(B) is the probability of the second event occurring.

• P(A ∪ B) = P(A) + P(B) - P(A∩B)

• The probability of an event not occurring is given by the formula:

P(not A) = 1 - P(A),

Where P(A) is the probability of the event occurring.

• Theorem of total probability:

Let S be a sample space and let A1 , A2, ...,An be a partition of S,

i.e. the events A1 , A2, ..., An are disjoint and their union is S. Let B be an event in S. Then the probability of B occurring is given by:

P(B) = P(B | A1 ) * P(A1 ) + P(B | A2) * P(A2) + ... + P(B | An) * P(An)

The questions given below – or ones similar to them – are likely to be asked.

Q.1: Calculate the probability for given situation

a. If a dice is thrown twice then estimate following:

1. Probability that the sum of numbers obtained is more than 8.

2. Probability that the number obtained is the prime number on both dice

3. Probability of not getting a one on either throw .

4. Probability of not getting the same number both times

b. A coin is tossed thrice. Calculate the probability of getting

1. At least two heads

2. Only one head

3. Same face

4. Only two tails

Q.2: Calculate the probability for a given situation

1. Evaluate P(A ∪ B) if 2 P(A) = P(B) = 5/8 and P(A/B) = 3/5
2. P and Q take turns to throw a pair of dice. P wins the game if he gets the total of 8 and Q wins the game if he gets the total of 9. If A starts the game then find the probability of B winning the game.
3. A family has two children. What is the conditional probability that both are girls if it is known that

1. One of them is a boy
2. The youngest is a girl
3. The older child is a boy

Also check - Class 12 Board Exams - Top Maths Formulae You Should Know