Mathematics In Aviation: Analysing Flight Trajectories

Have you ever looked up at the sky and been amazed by the way aeroplanes gracefully soar through the air?

As students in Class 11 and 12, you're about to embark on a journey of understanding mathematics that guides these flight paths. From the moment an aeroplane takes off to its smooth landing, it is pure mathematics that guides them through their journey. Let's dive into the captivating world of flight trajectories and uncover the mathematical marvels that make it all possible.

Role Of Mathematics In Aviation

An aeroplane trajectory is meticulously planned and analysed using mathematical concepts that stem from physics and aerodynamics. Mathematics isn't just a tool; it's the foundation upon which aviation operates.

In your physics journey, the concepts discussed in Class 11 and 12 NCERT chapters lay the groundwork for understanding flight trajectories. Chapter 3 of Class 11 Physics, "Motion in a Straight Line," introduces the basics of motion, displacement, velocity, and acceleration. As you move to Chapter 4, "Motion in a Plane," the discussion extends to vectors and projectile motion, which are essential for comprehending aviation.

In Class 12 Physics, Chapter 2, "Electrostatic Potential and Capacitance," introduces the concept of electric fields, which might not seem directly related to aviation at first glance. However, understanding the interconnectedness of seemingly diverse fields like physics is crucial in aviation engineering.

Also, Read - CBSE Class 10: How Quadratic Equations Can Help You Make A Shot In Basketball

Mathematics Behind Flight Trajectories

Projectile Motion: The Core Principle

Projectile motion is the bedrock of understanding flight trajectories. Imagine launching a ball into the air. The way it moves, rises, and falls follows specific mathematical patterns.

Let's examine a ball launched at an angle θ relative to the horizontal x-axis, having an initial velocity of u, as depicted below:

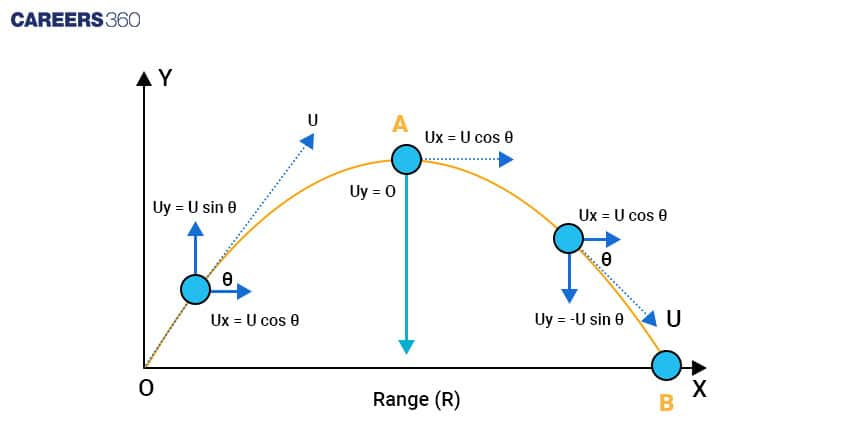
The point O is referred to as the projection point; θ represents the projection angle, and OB equals the Horizontal Range or, more simply, the Range. The complete duration taken by the object to travel from O to B is known as the time of flight.

To determine various factors linked to projectile motion, we can employ the differential equations of motion:

v = u - gt

s = ut - (1/2)gt2

v² = u² - 2gs

Where u is initial velocity, v is final velocity, s is displacement, and g is the acceleration due to gravity.

This is the same principle that governs the flight of aeroplanes. It's the magic that happens when an aircraft takes off and navigates through the sky.

Defining The Angle Of Attack

At the heart of aviation's mathematical intricacies lies the concept of the angle of attack. It is a crucial concept in aviation that influences how an aeroplane moves through the air. This angle, represented by ?, is the angle between the chord line of an aircraft's wing and the direction of motion through the air.

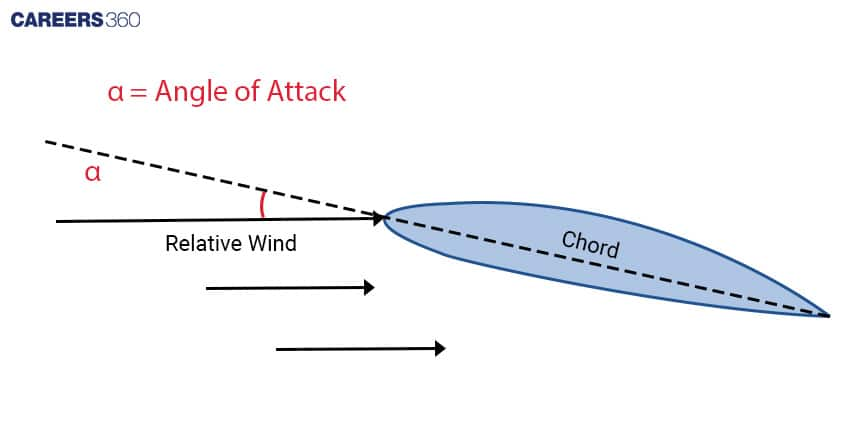
For a fixed-wing aircraft, this angle profoundly affects its lift, drag, and overall trajectory.

The equation that links the angle of attack, lift, and drag is:

F_lift = (1/2)C_LAV²

Here, F_lift is the lift force, C_L is the coefficient of lift, is the air density, A is area of wings, and V is the velocity of the aircraft.

Pilots adjust the angle of attack to control the lift and drag forces on the aeroplane. Too much or too little angle of attack can affect the aeroplane's stability and performance. In simpler terms, the angle of attack helps pilots steer the aeroplane smoothly and safely, making it a fundamental tool for successful flights.

Also Read - Why You Must Watch What You’re Eating - Understanding Autoimmunity From Class 12 Biology

Aspect Ratio: Unveiling The Wings Of Flight

Have you ever noticed the shape of aeroplane wings? They are not just there for show; they are designed with careful consideration of a concept called "aspect ratio." Aspect ratio is like a secret code that determines how efficient an aeroplane's wings are at producing lift and minimising drag.

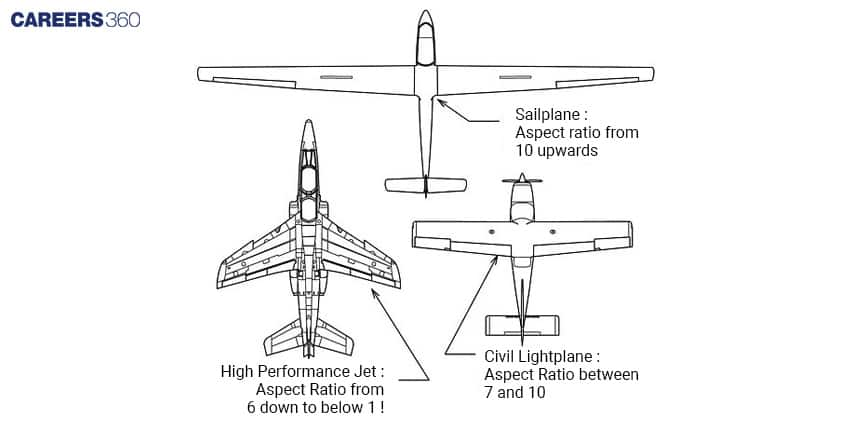
Imagine you're holding two sheets of paper. One is long and narrow, while the other is short and wide. If you try to flap both sheets up and down, you'll notice that the long and narrow one glides through the air more smoothly. This is the essence of the aspect ratio. It's the ratio of the wingspan (the length from tip to tip) to the average width of the wing.

Mathematically, the aspect ratio (AR) is calculated as

AR = Wingspan/(Average wing Width)

Now, let's consider an aeroplane with a wingspan of 40 metres and an average wing width of 4 metres. The aspect ratio would be:

AR = 40/4 = 10

So, the aspect ratio of this aeroplane is 10.

A higher aspect ratio generally means that the wings are long and narrow, which can make the aeroplane more efficient for flying long distances. Aeroplanes with high aspect ratios tend to have better lift-to-drag ratios, allowing them to glide through the air with less resistance.

Role Of Calculus: Understanding Changes

Calculus, often seen as a daunting subject, plays a significant role in aviation mathematics. Calculus helps us understand how things change over time or distance. When an aircraft changes its altitude or speed, calculus lets us analyse those changes precisely.

For instance, when calculating the rate of change of velocity with respect to time, we're essentially using calculus. The acceleration a ia the derivative of velocity v with respect to time t.

a = dv/dt

Calculating Flight Time And Altitude

Let's put our knowledge into practice with a real-world example. Suppose an aeroplane takes off at an angle of 30 degrees with respect to the ground. The initial velocity v₀ of the aeroplane is 200 m/s. We want how long the aeroplane will fly and how long it will stay in the air.

Solution:

Angle of takeoff θ = 30

Initial velocity v₀ = 200 m/s

g = 9.8 m/s² ≈ 10 m/s² (acceleration due to gravity)

We first find the vertical component of velocity using the sine function:

v_0y = v₀sin θ = 200 sin 30 = 200(1/2) = 20 m/s

The time of flight can be calculated using the kinematic equation:

T_flight = [2(v_0y)]/g = [2(20)]/10 = 4 sec

The maximum altitude can be calculated using the kinematic equation for vertical motion:

h_max = [(v_0y)²]/g = [(20)²]/10 = 400/10 = 40

This example shows how things like trigonometry, kinematic equations, and calculus come together to solve real problems in aviation.

If you want a paper plane to fly far, gently throw it at a nice angle, not too high or low. This angle is called the angle of attack. Also, make sure the wings aren't too short or too long – that's the aspect ratio. When you throw it, try to make it go straight instead of too much up or down. That's the projectile angle. And give it a good strong push at the start – that's the initial velocity. When you use all these ideas, your paper plane can go really far.

Practical Significance: Exams And Everyday Life

Acing Exams: Board, JEE, and NEET

As you prepare for exams like the board, JEE, and NEET, mastering the mathematics behind aviation isn't just about answering questions correctly. It's about developing a deeper understanding of physics and mathematics. Concepts like projectile motion, angle of attack, and calculus not only appear in direct questions but also influence your problem-solving skills across various topics.

Everyday Life Implications

Believe it or not, the mathematical concepts we've discussed have practical implications beyond the classroom and aviation. Problem-solving skills honed through aviation mathematics can help you analyse situations, make decisions, and solve challenges in everyday life. From predicting traffic flow to optimising travel routes, the mathematical toolkit you acquire from aviation studies equips you with valuable life skills.

Also Read - Think You Can Discover Good And Bad Carbohydrates? Think Again!

Hope you have now gained a comprehensive understanding of how mathematics plays a pivotal role in aviation and beyond. These concepts not only assist you in excelling during exams but also equip you to handle practical situations in your daily life.