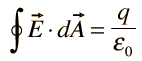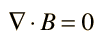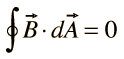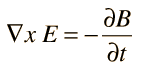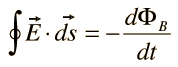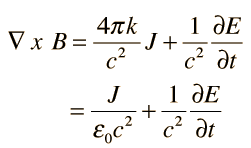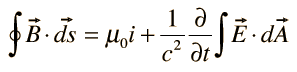Understanding Maxwell's Equations: A Mathematical Perspective

Electricity and magnetism are two fundamental forces that govern the behaviour of our everyday world. From the flickering of light bulbs to the functioning of electronic devices, these forces play a crucial role. In the 19th century, a Scottish physicist named James Clerk Maxwell revolutionised our understanding of electricity and magnetism by formulating a set of equations known as Maxwell's equations. These equations elegantly describe the intricate relationship between electric and magnetic fields, laying the foundation for the field of electromagnetism.

Maxwell's equations are a powerful tool that allows us to comprehend how electric and magnetic fields interact and propagate through space. They provide a mathematical framework for understanding a wide range of phenomena, from the generation and transmission of electrical power to the behaviour of electromagnetic waves, which include radio waves, microwaves, and even visible light.

In the NCERT Physics textbooks for Class 11 and Class 12, the concepts related to Maxwell's equations are used in various chapters including:

• Chapter 1: Electric Charges and Fields

  • Gauss's Law for Electricity (Gauss's Law)

• Chapter 2: Electrostatic Potential and Capacitance

  • Gauss's Law for Electricity (Gauss's Law)

• Chapter 4: Moving Charges and Magnetism

  • Gauss's Law for Magnetism

• Chapter 5: Magnetism and Matter

  • Gauss's Law for Magnetism

• Chapter 6: Electromagnetic Induction

  • Faraday's Law of Electromagnetic Induction

• Chapter 7: Alternating Current

  • Ampère-Maxwell Law

• Chapter 8: Electromagnetic Waves

  • Maxwell's Equations (all four equations)

Therefore, Understanding and having a good command of Maxwell's equations can greatly assist students in solving various problems in exams such as NEET, JEE, CBSE, and state boards. Following are four equations of Maxwell in differential and integral form.

Let's discuss one by one in detail.

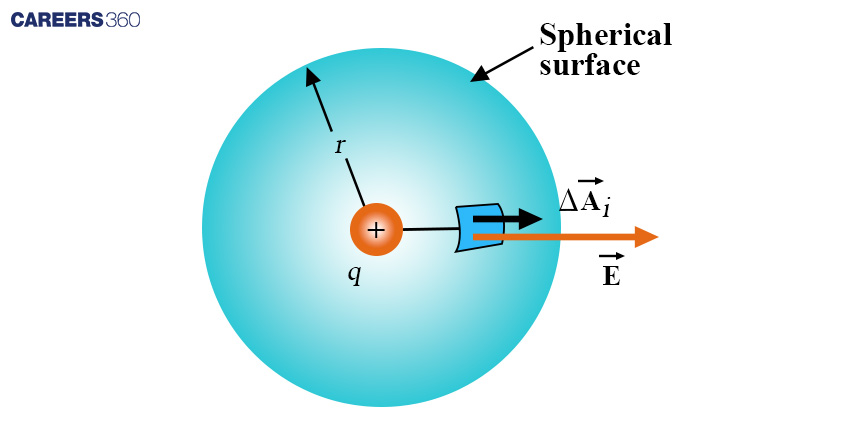
Gauss's Law for Electricity

Differential form: Consider a closed surface A enclosing a volume V. According to Gauss's Law for Electricity, the electric flux passing through the closed surface A is equal to the net electric charge enclosed by the surface divided by the electric constant (ε₀).

Also Check - Discover How Mathematics Helps Calculate Plot Areas Accurately

Mathematically, it can be represented as:

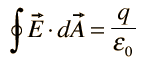
Using the divergence theorem,which relates the surface integral of the dot product of a vector field and the outward normal vector over a closed surface to the volume integral of the divergence of that vector field over the volume enclosed by the surface.

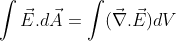
Now, the above equation can be rewritten as:

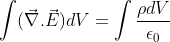
Since the volume V can be chosen arbitrarily, the integrands on both sides of the equation must be equal. Therefore, we obtain the differential form of Gauss's Law for Electricity:

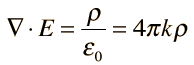
Where, E represents the divergence of the electric field (E), ρ is the charge density, and ε₀ is the electric constant.

Integral form: The integral form of Gauss's Law for Electricity is obtained by integrating the differential form over a closed surface A. Mathematically, it is represented as:

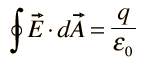
Gauss's Law for Magnetism:

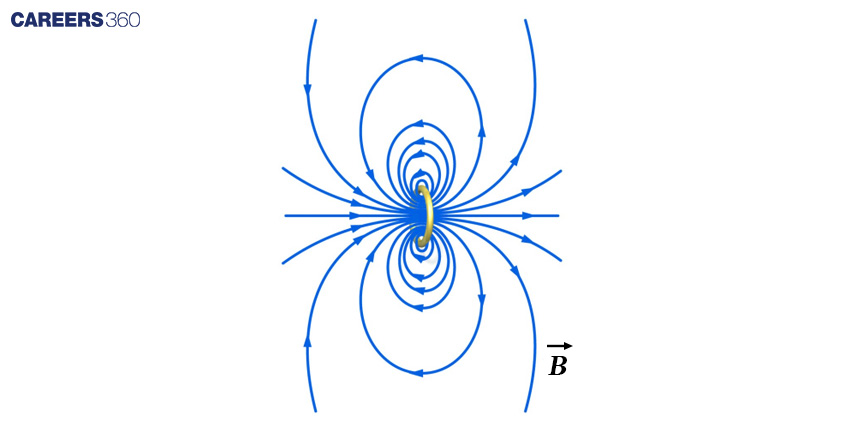
Differential form: According to Gauss's Law for Magnetism, the net magnetic flux passing through any closed surface is always zero.

Mathematically, it can be represented as:

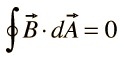
Using the diversion theorem

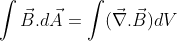
This law implies that there are no magnetic monopoles and that magnetic field lines always form closed loops.

Integral form: The integral form of Gauss's Law for Magnetism is obtained by integrating the differential form over a closed surface S. Mathematically, it is represented as:

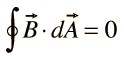
This equation states that the net magnetic flux passing through any closed surface is always zero.

Faraday's Law of Electromagnetic Induction

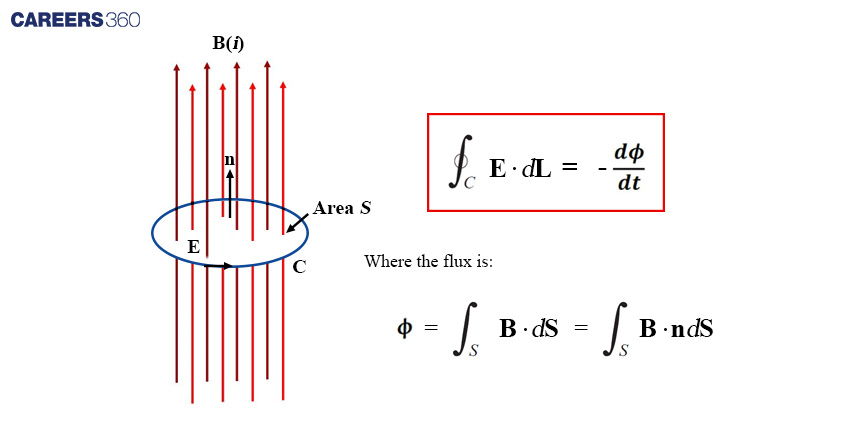
Differential form: Faraday's Law of Electromagnetic Induction describes how a changing magnetic field induces an electric field.

Also Check - What Is A Forest’s Microclimate And How Does It Impact The Environment?

Mathematically, it can be represented as:

We know that

Applying stoke’s theorem on L.H.S

The equation can be rewrite as

Where ∮ represents the closed path, E is the electric field, dl is an infinitesimal vector element along the path, ∮_S represents the surface enclosed by the path, B is the magnetic field, and dt is the time differential.

Integral form: The integral form of Faraday's Law of Electromagnetic Induction is obtained by integrating the differential form over a closed path C. Mathematically, it is represented as:

This equation states that the electromotive force (emf) around a closed path is equal to the negative rate of change of the magnetic flux through the surface enclosed by the path.

Ampère-Maxwell Law

Differential form: Ampère's Law describes the relationship between the magnetic field and the electric current. However, Maxwell added an additional term to Ampère's Law, known as the displacement current, to make it consistent with Faraday's Law. Mathematically, the Ampère-Maxwell Law is represented as:

Where ∇×B represents the curl of the magnetic field (B), μ₀ is the magnetic constant (permeability of vacuum), J represents the current density, and ∂Edtrepresents the rate of change of the electric field (E) with respect to time.

The differential form of the Ampère-Maxwell Law is derived by considering a closed loop C and applying Stoke's theorem. The left-hand side of the equation can be written as:

By equating the integrands on both sides, we obtain the differential form of the Ampère-Maxwell Law:

Integral form: The integral form of the Ampère-Maxwell Law is obtained by integrating the differential form over a closed loop C. Mathematically, it is represented as:

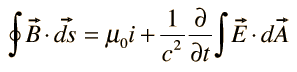
This equation states that the circulation of the magnetic field around a closed loop is equal to the sum of the current passing through the loop and the rate of change of the electric flux through any surface bounded by the loop.

Hope, you have now a good understanding of Maxwell's equations and their use in different concepts of Class 12.