Probability For Class 12: Can You Predict Who Will Win The Cricket World Cup?

As another exhilarating edition of ICC Cricket World Cup drew to a close, we couldn’t help but wonder why India’s “Men in Blue”, who were amongst the favourites to win the World Cup, could not actually do so. From top-ranked batters to world-class bowlers and fielders, we had it all. But still, we could not get the result. So, as students of mathematics, we might ask the question: “Can we quantify the chances of our team winning the World Cup in the next edition using the concepts of probability?”

This Story also Contains

1. How is win probability calculated in Cricket
2. Probability And Cricket World Cup
3. Cricket win probability

The answer is, “Yes”. That is precisely what we are going to explore now. We will learn the concepts of conditional and total probability by applying them to the World Cup tournament set up.

As this is for students, we will keep the format of our tournament simple and make some assumptions that will reduce the complexity and calculations.

How is win probability calculated in Cricket

FORMAT-1

Let us frame the rules or assumptions of the first simplistic tournament. These are:

· We are already in the semi-final stage of the tournament

· Four teams have qualified for the semi- finals,

o Group A: India (Group toppers), Pakistan (Second best)

o Group B: Australia (Group toppers), England (Second best)

· Each team has equal chances of winning any match, that is, the probability of any team winning a particular match is ½.

· Australia faces Pakistan in the first semi-final; India faces England in second semi-final

· Winners of the semi-finals play the final.

Now, for India to win the World Cup, its team must win its semi-final, for which the probability is 1/2.

Then it must win the final against the winner of the first semi-final. Now, as the chances of India winning against Australia or Pakistan are the same, so, chances of India winning the final is again 1/2.

Using conditional probability, the probability of India winning the World Cup will equal the multiplication of two probabilities: probability of India winning the semi-final and probability of India winning the final.

So, the probability of India winning the World Cup will be (1/2) (1/2) = 1/4. This means India has one in four chances of winning the world cup. Similarly, all other teams too will have the same chance of winning the World Cup under these assumptions.

It can also be seen from the classical definition of probability: where there are a total of four equally strong teams, the probability of one particular team winning the world cup will be 1/4.

Also Read,

• How To Become An Indian Olympiad Qualifier In Physics
• Maths Made Easy: Simple Interest And Compound Interest Explained
• JEE Main: How To Prepare At Home, Without Spending A Paisa
• Low-Cost Commerce Courses After 10+2

Probability And Cricket World Cup

FORMAT-2

Now, we have 8 teams at the start of the tournament, and the tournament is in knock-out format.

The rules/assumptions for this case are as follows:

· There will be 4 matches in the quarter final stage between 8 teams, out of which 4 winners will play 2 semi-finals.

· The winners of the semi-finals will play in the final.

· Each team is of equal strength, and the probability of each team winning each game they play is half (1/2)

· So, the probability for India winning the quarter finals is 1/2

· The probability of India winning the semi-final is 1/2

· The probability of India winning the final is 1/2

Using conditional probability, total probability of India winning the World Cup in this case will be 1/2 x 1/2 x 1/2 = 1/8

Cricket win probability

FORMAT-3

Now, let’s make our hypothetical tournament a little more interesting. Let us say group toppers have an edge in semi-finals, as they are more confident because of their better performance in the group stage. So, the new rules and assumptions of the tournament are

· We are already in the semi-final stage

· Four teams have qualified for the semi- finals,

o Group A: India (Group toppers), Pakistan (Second best)

o Group B: Australia (Group toppers), England (Second best)

· Australia faces Pakistan in the first semi-final, and India faces England in the second semi-final.

· Winners of the semi-finals play the final

· Probability of any group-topper team winning against a second-best team in the group is 0.6, as they are more confident because of their better performance in the group stage. We can assume any number larger than 0.5 (and less than 1), so for simplicity we are assuming the value of 0.6

· If both group-toppers meet in the final, they have equal chances of winning the final (that is, ½ or 0.5 probability of winning for each)

· Similarly, if both second-best teams meet in the final, they have equal chances of winning (0.5 probability of winning for each)

· But, as India-Pakistan rivalry is special and India usually wins over Pakistan when they meet in any world cup, so if India meets Pakistan in the final, then we can assume that the chances of India winning is 0.7 (it could have been 0.8, but the loss in the 2021 T-20 World Cup has reduced our team’s confidence a bit).

This format, from the perspective of India, can be seen in an easier way through the following tree-diagram

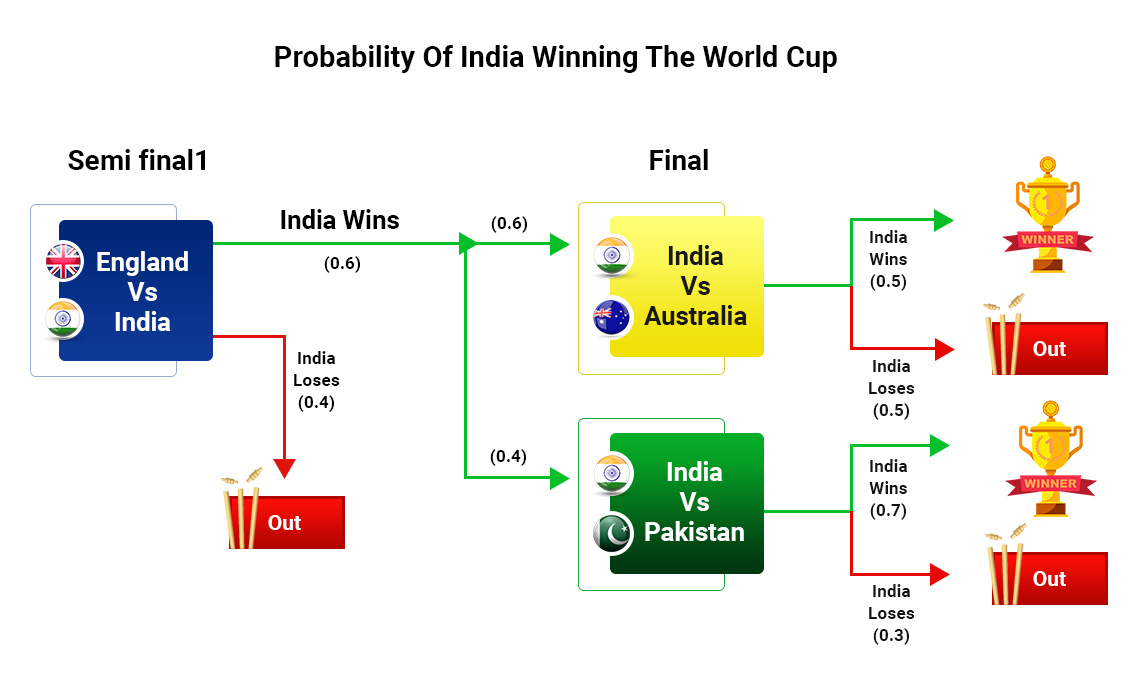Probability of India winning the World Cup

Now, to calculate the probability of India winning: India has to first win the semi-final against England. And the probability of this happening is 0.6 as India was a group topper.

Then, India can take either of the two green paths as indicated in the diagram. The upper path in the diagram corresponds to the India Vs Australia match, which will happen if Australia defeats Pakistan in the semi-finals. The probability of Australia winning in the semi-final is 0.6 as it was the group-topper at the group stage. Then, in the India Vs Australia final, chances of India winning will be 0.5 as both India and Australia had been group toppers.

If this path is followed, then the probability of India winning the World Cup is 0.6 x 0.5 (=0.3). This is the conditional probability, in which two probabilities are multiplied:

(Chances of India Vs Australia match to happen in the final) x (chances of India winning if India Vs Australia match happens) .

The lower path is also possible, which corresponds to the India Vs Pakistan match which will happen if Pakistan defeats Australia in the semi-finals. The probability of Pakistan winning in the semi-final is 0.4, as Pakistan was the second-best team at group stage. Then in the India Vs Pakistan final, chances of India winning will be 0.7 as we have assumed for the India-Pakistan match. So, if this path is followed, then the probability of India winning the world cup is 0.4 x 0.7 (=0.28).

Now, as India may win using either of the paths described above, we can add these probabilities. This is called Total Probability Theorem. If India enters the final, then chances of it winning is 0.3 + 0.28 = 0.58

But still, this does not equal the probability of India winning the World Cup. As it is not certain that India will defeat England in the semi-final. So, again we will have to use conditional probability and multiply two probabilities: Probability of India winning against England in semi-finals (0.6) with probability of India winning if it enters the final (0.58). So, The overall chances of India winning will be:

(0.6) x (0.58) = 0.348

In this scenario, the chances of India winning will be higher as compared to first tournament where it was 0.25

Now, apart from concepts of Probability, what else can we learn from this exercise?

First, we can see that the chances of a strong team winning the World Cup even after getting to the semi final stage are not astronomically high, so we must support our team even if they could not win. Second, as a student preparing for an exam which is one of the most competitive, we must not just look at the odds against us and be discouraged. As the old adage goes, “fortune favours the brave” and we must keep on striving and working hard with the right guidance to achieve the goal that we have set for ourselves.