Ideal Gas Laws: Mathematical Relationships In Gaseous Systems

The Ideal Gas Laws are a fundamental concept in the study of gases, which helps us understand the behaviour of gases under different conditions. It provides a mathematical relationship between the pressure, volume, temperature, and amount of a gas in a system. The Ideal Gas Law is a crucial topic in both subjects of Physics and Chemistry for students studying in Class 12 and preparing for competitive exams like State Boards, CBSE, NEET, IIT JEE, or higher studies. It not only forms the basis of many advanced concepts in physics and chemistry but also finds practical applications in various real-life scenarios.

In this article, we'll explore the mathematical principles behind the Ideal Gas Law and other gas laws, along with practical examples. We'll also examine how these laws are applied in our everyday lives.

Explanation And Importance

The Ideal Gas Law is based on the assumption that a gas consists of a large number of tiny particles that are in constant random motion. It helps us understand how these gas particles behave under different conditions, such as changes in temperature, pressure, or volume. The law is particularly useful for predicting the behaviour of gases when they undergo changes, such as expansion, compression, or heating.

The Ideal Gas Law can be expressed mathematically as: PV = nRT

Where:

• P represents the pressure of the gas (measured in units such as Pascal, atm, or mm of Hg)

• V represents the volume of the gas (measured in units such as litres or cubic metres)

• n represents the number of moles of gas present in the system

• R represents the ideal gas constant (which has a specific value depending on the units used)

• T represents the temperature of the gas (measured in Kelvin).

By rearranging the equation, we can derive various other useful equations that help us solve problems related to gases. For example, we can calculate the amount of gas present using the equation: n = PV/RT

This equation allows us to determine the number of moles of gas based on its pressure, volume, and temperature. It is particularly useful when dealing with stoichiometry problems in chemistry.

Let's consider an example to illustrate the application of the Ideal Gas Law. Suppose we have a gas sample with a volume of two litres, a pressure of three atmospheres, and a temperature of 300 Kelvin.

We can use the Ideal Gas Law equation to find the number of moles of gas present. Assuming the ideal gas constant R to be 0.0821 atm·L/mol·K, we can calculate as follows:

n = PV/RT

n = (3 atm 2 L)/[(0.0821 atm L/Mol K) 300 K]

n = 0.24 Moles

In this example, we determined that the gas sample contains approximately 0.24 moles of gas based on the given conditions.

Other Gas Laws

In addition to the Ideal Gas Law, there are several other important gas laws that help us understand and predict the behaviour of gases. Let's explore some of these laws, along with their mathematical expressions and practical examples.

Boyle's Law

Boyle's Law states that the pressure of a given amount of gas is inversely proportional to its volume at constant temperature.

Mathematically, it can be expressed as: P₁V₁ = P₂V₂

Here, P₁ and V₁ represent the initial pressure and volume, while P₂ and V₂ represent the final pressure and volume of the gas.

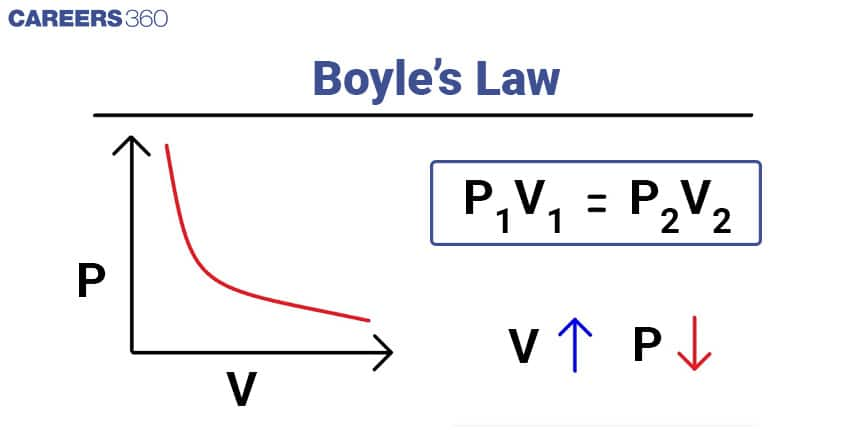
For example, suppose we have a gas in a container with an initial volume of 2 litres and a pressure of 1 atmosphere. If the volume is reduced to 1 litre while keeping the temperature constant, we can calculate the final pressure using Boyle's Law as follows:

P₁V₁ = P₂V₂

1 atm 2 L = P₂ 1 L

2 atm = P₂

In this case, the final pressure of the gas would be 2 atmospheres.

Charles's Law

Charles's Law states that the volume of a given amount of gas is directly proportional to its temperature at constant pressure.

Mathematically, it can be expressed as: V₁/T₁ = V₂/T₂

Here, V₁ and T₁ represent the initial volume and temperature, while V₂ and T₂ represent the final volume and temperature of the gas (in Kelvin).

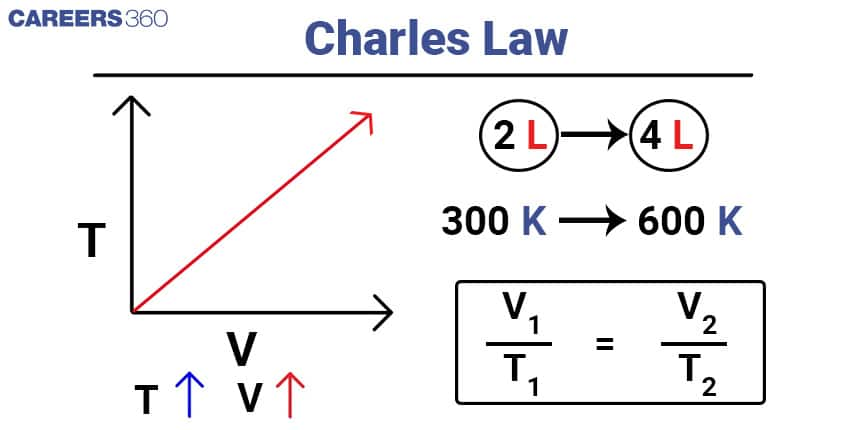
For example, let's consider a gas sample with an initial volume of two litres and a temperature of 273 Kelvin. If the temperature is increased to 300 Kelvin while maintaining constant pressure, we can calculate the final volume using Charles's Law as follows:

V₁/T₁ = V₂/T₂

2L / 273K = V₂ / 300K

V₂ = 2.34 L

In this case, the final volume of the gas would be approximately 2.34 litres.

Also check - What Are The Effects Of Drug Abuse On Your Physical And Mental Health?

Avogadro's Law

Avogadro's Law states that equal volumes of gases, at the same temperature and pressure, contain an equal number of particles (atoms, molecules, or ions).

It can be expressed mathematically as: V₁/n₁ = V₂/n₂

Here, V₁ and n₁ represent the initial volume and number of moles, while V₂ and n₂ represent the final volume and number of moles of the gas.

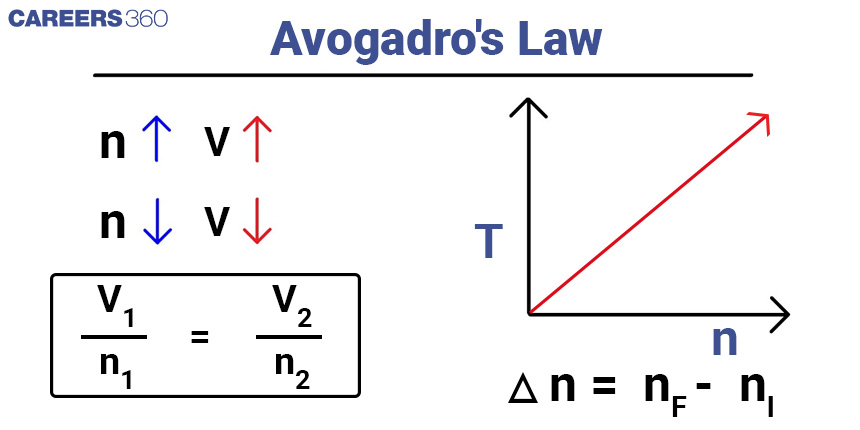
For instance, consider a gas sample with an initial volume of two litres and one mole of gas particles. If the number of moles is doubled to two moles while maintaining constant temperature and pressure, we can calculate the final volume using Avogadro's Law as follows:

V₁/n₁ = V₂/n₂

2L/1 Mol = V₂/2 Mol

V₂ = 4 L

In this case, the final volume of the gas would be approximately 4 litres.

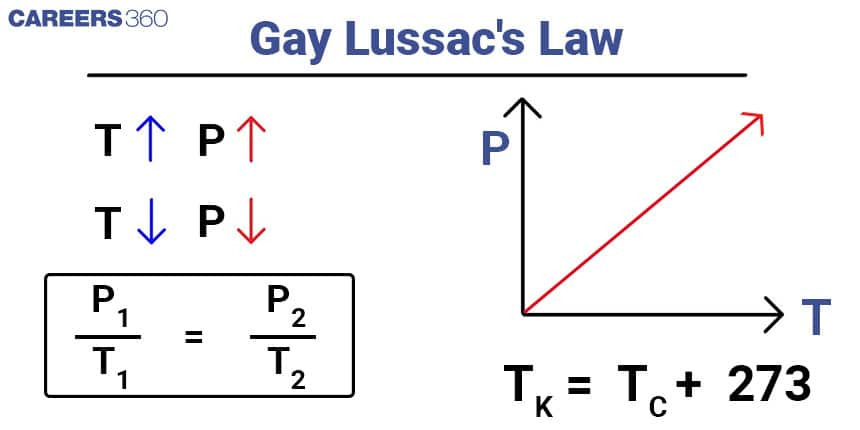
Gay-Lussac's Law

Gay-Lussac's Law, also known as the Pressure Law, states that the pressure of a given amount of gas is directly proportional to its temperature at constant volume. Mathematically, it can be expressed as: P1T1=P2T2

Also check - Decoding The Physics Behind Bicycle Derailleur Systems

Everyday Applications Of The Ideal Gas Law

• Balloons: Students often come across balloons filled with gas, such as helium or hydrogen. The Ideal Gas Law helps them understand how the volume, pressure, temperature, and amount of gas inside the balloon are interrelated. They can apply this knowledge to predict the behaviour of balloons in different conditions.

• Scuba Diving: Understanding the Ideal Gas Law is crucial for scuba divers. It helps them comprehend how the volume of a gas (such as compressed air) changes with pressure and temperature as they descend or ascend underwater. This knowledge aids in safe diving practices and avoiding decompression sickness.

• Airbags in Vehicles: Airbags in cars are designed to inflate rapidly in the event of a collision. The Ideal Gas Law plays a role in the design and functioning of these safety devices. By understanding the relationship between gas pressure, volume, and temperature, students can appreciate how airbags protect passengers during an impact.

• Gas Cylinders: Many households use gas cylinders for cooking or heating purposes. Students can apply the Ideal Gas Law to understand how the pressure and volume of gas change as it is consumed from the cylinder. This knowledge can help them estimate the amount of gas remaining and plan for refills accordingly.

• Cooking: Cooking involves various gas-related processes, such as baking, boiling, and steaming. By applying the Ideal Gas Law, students can comprehend how temperature and pressure affect the volume of gases involved in these cooking methods. This knowledge helps them regulate cooking times and temperatures for better culinary outcomes.