Exploring The Cosmos: How Mathematics Powers Space Travel

For centuries, human beings have been fascinated about the cosmos. From ancient times, people have looked up at the stars and wondered what lies beyond our planet. With the advancements in technology and the ever-evolving understanding of the laws of physics, space travel has become a reality. However, what many people may not realise is that the foundation of space travel is built upon the language of mathematics.

Mathematics is the tool that allows scientists and engineers to calculate trajectories, predict orbits, and design spacecraft. From the initial launch to the landing on a distant planet, every aspect of space travel is meticulously planned and executed using complex mathematical calculations.

This article will explore the various ways in which mathematics powers space travel. It will delve into the fundamental principles of calculus, geometry, and algebra that underpin space exploration. From the orbital mechanics that govern the motion of planets and spacecraft to the intricacies of rocket propulsion, we will examine how mathematics is used to make space travel a reality.

Also check - How Mathematics Is Useful In Landslide Risk Assessment: A Case Study Of Joshimath

Fundamental Principles That Help Space Exploration

There are several fundamental principles that underpin space exploration, and these principles are based on the laws of physics and mathematics. Some of the key principles are:

Mathematical Principles

Space exploration is built upon several fundamental mathematical principles. Here are some of the key mathematical principles that underpin space exploration:

1. Calculus - deals with the study of rates of change. In space exploration, calculus is used to calculate the velocity, acceleration, and position of objects in space. For example, when launching a spacecraft, calculus is used to calculate the optimal trajectory that will allow the spacecraft to reach its destination using the least amount of fuel. The laws of physics governing orbital mechanics also rely heavily on calculus. By solving differential equations, which are the foundation of calculus, scientists can predict the motion of planets, asteroids, and spacecraft.

2. Geometry - deals with the study of shapes. In space exploration, the position and orientation of spacecraft and other objects in space are determined using geometric principles. For example, the location of a planet can be calculated using the angle between it and a distant star.

3. Algebra - deals with the study of mathematical symbols and the rules for manipulating them. In space exploration, algebraic equations are used to determine the optimal size and shape of spacecraft components, such as fuel tanks and engines.

4. Trigonometry - deals with the study of triangles and the relationships between their sides and angles. In space exploration, trigonometry is used to calculate the distances between objects in space. For example, the distance between a spacecraft and a planet can be calculated using the angle between the planet and a distant star.

5. Probability theory - deals with the study of random events and the likelihood of their occurrence. In space exploration, probability theory is used to predict the likelihood of certain events occurring, such as the probability of a spacecraft encountering an asteroid.

Designing Of Spacecraft

How is mathematics crucial in designing a spacecraft? Engineers use mathematical principles such as calculus, algebra, and geometry to design spacecraft components, including fuel tanks and engines. Algebraic equations are used to determine the optimal size and shape of these components, ensuring that they are efficient and reliable.

Another crucial aspect of spacecraft design is aerodynamics, which is the study of how objects move through fluids. Mathematics is used to model the flow of air around the spacecraft and predict how it will behave in different environments, including the vacuum of space. This allows engineers to design spacecraft that can withstand the extreme conditions of spaceflight.

Moreover, mathematicians and engineers also use numerical simulations to design spacecraft. These simulations allow them to test different design concepts and see how they would perform in real-world conditions. By running simulations and analysing the results, engineers can optimise the design of a spacecraft to ensure that it meets its mission requirements.

Also check - Collagen Protein Vs Whey Protein: The Biology Behind Bulking Up

Launching A Spacecraft

Rocket propulsion is based on the principle of conservation of momentum. According to this principle, the total momentum of a system remains constant if there are no external forces acting on the system. This means that if an object with mass m1 moves with velocity v1, and another object with mass m2 moves with velocity v2, then the total momentum of the system is given by:

P = m₁v₁ + m₂v₂

Now let's consider at the beginning of the launch, the rocket's total mass is made up of M, the empty rocket's mass, and Δm, the fuel's mass. The system is moving at a velocity V relative to an observer on earth. The total initial momentum of the rocket can be calculated by multiplying the mass by the velocity.

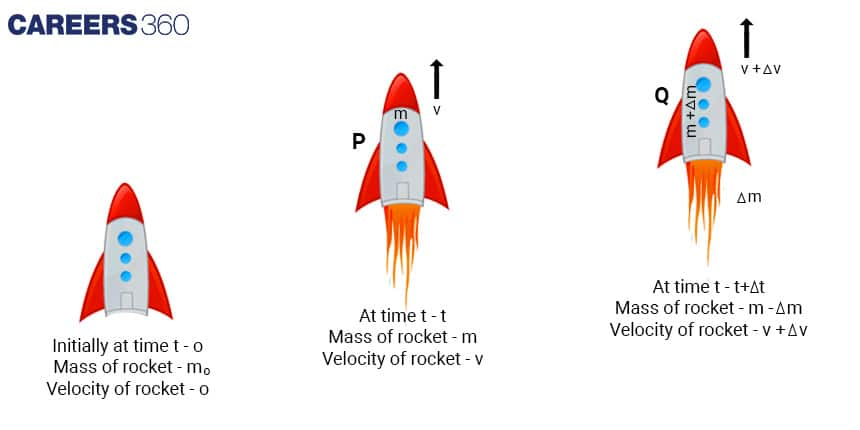
When the rocket's engine ignites at time T, the fuel is burned and ejected, causing the rocket to gain velocity. The rocket's velocity becomes V + ΔV, and the velocity of the exhaust becomes V_e, relative to an observer on earth. The total final momentum of the rocket can be calculated by adding the momentum of the rocket and the exhaust.

Since there is no external force acting on the rocket, the net force is zero, and the total change in momentum from t=0 to t=T will be zero. Therefore, change in momentum P_f - P_i = 0.

This equation can be simplified to MΔV - ΔmV_e = 0, where Ve is the relative velocity of the exhaust with respect to the rocket.

By understanding that Δm results in a decrease in the total mass of the rocket system, Δm can be replaced with -dm. Further considering an infinitesimal time difference dt from time t = 0 to t = T, ΔV can be replaced with dv. The final equation can then be simplified to dV = - V_edm/M.

By integrating this equation over the small-time interval dt from the final state to the initial state and noting that the integral of dx/X is ln X,

we can obtain the final equation V_f - V_i = V_e ln(M_i / M_f)

where Vf and Vi are the final and initial velocities, respectively, and Mi and Mf are the initial and final masses of the rocket system.

Navigation Of Spacecrafts

When a spacecraft travels through space, it follows a particular path, or trajectory, based on a few different factors. These include the initial velocity of the spacecraft, the gravitational pull of nearby objects like planets or stars, and the thrust from any engines or rockets on the spacecraft.

To calculate the trajectory of a spacecraft, we can use a few different mathematical equations. Here are a few key ones:

1. The equation for velocity: v = u + at

This equation tells us how fast the spacecraft is moving (its velocity) based on its initial velocity (u), the acceleration of the spacecraft (a), and the amount of time that has passed (t).

2. The equation for acceleration due to gravity: a = (GM/r²)

This equation tells us the acceleration of the spacecraft due to the gravitational pull of a nearby object (like a planet or star). G is the gravitational constant, M is the mass of the nearby object, and r is the distance between the spacecraft and the object.

3. The equation for circular orbit: v = √(GM/r)

This equation tells us the velocity of the spacecraft needed to maintain a circular orbit around a nearby object, where G, M, and r are the same as in the previous equation.

4. The equation for escape velocity: v = √(2GM/r)

This equation tells us the velocity the spacecraft needs to achieve in order to escape the gravitational pull of a nearby object and continue on its own path through space.

By using these equations, we can calculate the trajectory of a spacecraft as it moves through space, taking into account the various factors that affect its path.

Mathematics plays a critical role in the design, planning, and execution of space missions, including spacecraft launches. Class 12 students who aspire to pursue careers in space should strive to get a good grasp of mathematics as it will enable them to contribute to the development of innovative space technologies and make significant contributions to the field of space exploration.