From GDP To Gini Coefficient: Understanding Economic Indicators Through Class 12 Maths

Economic Indicators

Here are some of the most commonly used economic indicators:

Gross Domestic Product (GDP)

The GDP, which stands for Gross Domestic Product, is a metric used to quantify the overall value of all goods and services that are produced within the geographic boundaries of a country over a specified period, typically a year. This metric is widely regarded as a critical gauge of a nation's economic performance. In Class 12, students study the various methods of calculating GDP. Here we will discuss the four methods of calculating GDP along with the mathematical calculations.

1. Expenditure Method

2. Income Method

3. Production Method

4. Value-added Method

1. Expenditure Method

In this method, GDP is calculated by adding up all the expenditures made on the purchase of goods and services within a country during a specific period. The mathematical formula for calculating GDP using the expenditure method is:

GDP = C + I + G + (X-M)

Where:

C = Personal consumption expenditures

I = Gross private domestic investment

G = Government consumption expenditures and gross investment

X = Exports of goods and services

M = Imports of goods and services

To illustrate the calculation of GDP, let's consider the following hypothetical example:

Suppose a country produces the following goods and services in a year:

• Personal consumption expenditures (C): ₹500 billion

• Gross private domestic investment (I): ₹200 billion

• Government consumption expenditures and gross investment (G): ₹300 billion

• Exports of goods and services (X): ₹100 billion

• Imports of goods and services (M): ₹50 billion

Then, using the formula above, we can calculate the GDP as follows:

GDP = C + I + G + (X - M)

= ₹500 billion + ₹200 billion + ₹300 billion + (₹100 billion - ₹50 billion)

= ₹1,050 billion

Therefore, the GDP of this hypothetical country is ₹1,050 billion. This is a measure of the total economic output of the country over the specified period.

2. Income Method

In this method, GDP is calculated by adding up all the incomes generated by the production of goods and services within a country during a specific period. The mathematical formula for calculating GDP using the income method is:

GDP = W + R + I + P

Where, W = Wages and Salaries,

R = Rent,

I = Interest,

P = Profits

3. Production Method

In this method, GDP is calculated by summing up the value of all goods and services produced within the country's borders during a specific period. This is also known as the output method. The mathematical formula for calculating GDP using the production method is:

GDP = VA + T - S

Where, VA = Value Added,

T = Indirect Taxes,

S = Subsidies

4. Value-added Method

In this method, GDP is calculated by adding up the value added at each stage of production. The mathematical formula for calculating GDP using the value-added method is:

GDP = VA₁ + VA₂ + VA₃ + ... + VA_n

Where, VA₁, VA₂, VA₃, ..., VA_n are the value added at each stage of production.

Also Read | Unlock The Secrets Of Cryptography With The Help Of Mathematics

Gini Coefficient

The Gini Coefficient is a measure of inequality of a distribution, widely used in economics and social sciences. It is a number between 0 and 1, where 0 represents perfect equality (everyone has the same income or wealth) and 1 represents perfect inequality (one person has all the income or wealth).

The Gini Coefficient can be calculated using the following formula:

G = (A / (A + B))

Where A is the area between the Lorenz curve and the line of perfect equality (the diagonal line), and B is the area between the Lorenz curve and the horizontal axis (the line of perfect inequality).

The Lorenz curve is a graph that shows the cumulative percentage of a population on the horizontal axis, ranked by income or wealth, and the cumulative percentage of income or wealth they hold on the vertical axis. The Lorenz curve is always below the line of perfect equality and above the line of perfect inequality.

Suppose we have data on the income distribution of a country, and we have calculated the cumulative percentage of the population and the cumulative percentage of income as follows:

Lorenz Curve of above data

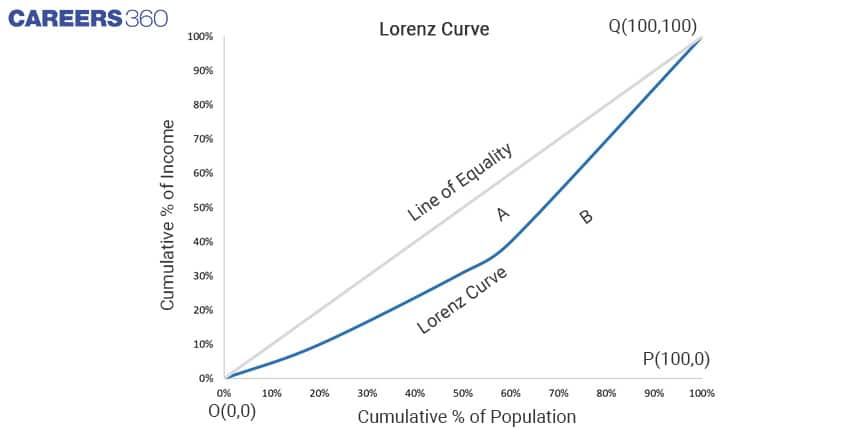
Also Read | Understanding Inflation: A Class 12 Maths Concept

We can calculate the area using the Trapezoidal Rule which evaluates the area under the curves by dividing the total area into smaller trapezoids rather than using rectangles.

Area of trapezium = ½(sum of parallel lines)(height between parallel lines)

A + B = Area of triangle OPQ

A + B = ½(100)(100) = 5000

Area B is simply the area between the Lorenz curve and the x-axis.

B = ½(1)(10) + ½(3 + 1)(10) + ½(6 + 4)(10) + ½(10 + 6)(10) + ½(15 + 10)(10 + ½(21 + 15)(10 + ½(28 + 21)10 + ½(37 + 28)10 + ½(51 + 37)10 + ½(100 + 51)10

= 5 + 20 + 50 + 80 + 125 + 180 + 245 + 325 + 755

= 1785

To calculate A, we first need to calculate the area between the Lorenz curve and the line of perfect equality.

A = 5000 - 1785 = 3215

Finally, we can calculate the Gini Coefficient:

G = A / (A + B)

G = 3215 / (5000)

G = 0.643

This means that the income distribution in this country is highly unequal, with almost all the income concentrated in the hands of a few individuals.

Economic indicators such as GDP and the Gini Coefficient are vital tools for understanding the performance and health of a country's economy. While GDP measures the total value of goods and services produced within a country's borders over a specified period, the Gini Coefficient measures how this income is distributed within the society. Maths play an important role in determining these vital tools of the economy.