Understanding Harmonic Motion: A Differential Equations Approach

Harmonic motion is a fascinating and essential topic in physics and mathematics that finds its applications in various fields, including engineering, music, and even biology. The study of harmonic motion involves understanding the behaviour of oscillating systems, such as springs, pendulums, and vibrating strings. It is a cyclic motion where the restoring force is proportional to the displacement, making it a crucial example of a linear dynamic system.

In this article, we will explore harmonic motion from a differential equations perspective, delving into the underlying mathematical concepts. We will also discuss how a profound understanding of these concepts can significantly benefit Class 11 and Class 12 students, especially those preparing for competitive exams such as JEE, NEET, CBSE, and State boards.

Mathematics Of Harmonic Motion

Harmonic motion is governed by a second-order linear differential equation. For any oscillating system, the differential equation can be represented as

d²x/dt² + ω²x = 0

d²θ/dt²+ω²θ= 0

Where:

• x, θ represents the displacement of the oscillating particle from its equilibrium position at time t.

• ω is the angular frequency of the oscillation.

The solution to this differential equation is of the form:

x_(t) = A sin(ωt + φ)

θ_(t) = θ₀sin(ωt + φ)

Where:

• A and θ₀ are the amplitude of the motion.

• φ is the phase angle, which depends on the initial conditions of the system.

The equation reveals that harmonic motion is sinusoidal, characterised by the cosine function. The oscillations repeat themselves over time, and the angular frequency ω determines how quickly these oscillations occur.

Simple Harmonic Motion

When a system experiences a restoring force proportional to the displacement and directed opposite to it, it undergoes SHM. It is an idealised form of harmonic motion and can be observed in systems like a mass-spring system.

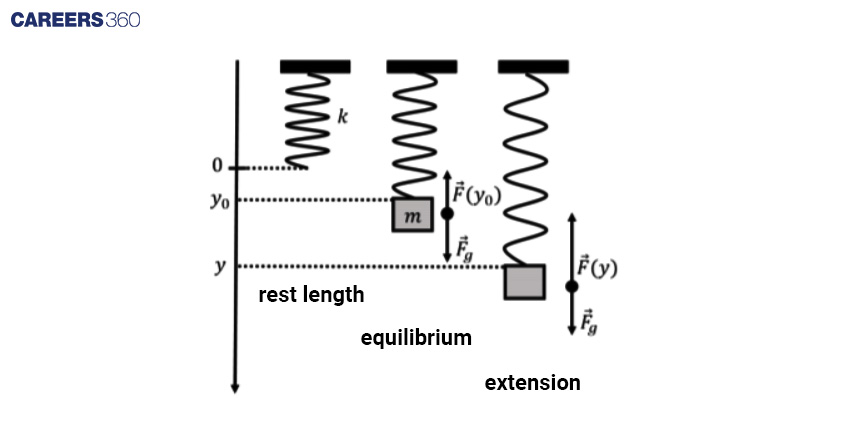
Restoring force is given as

F = -ky

We know that F = ma

Therefore,

ma = -ky

a = -(k/m)y

d²y/dt² = -(k/m)y

Thus, differential equation for SHM can be written as

d²y/dt² + (k/m) y = 0

Where:

• k is the spring constant.

• m is the mass attached to the spring.

The angular frequency ω in this case, is given by ω = √(k/m). By studying this equation, students can gain insights into how the mass-spring systems behave under the influence of different parameters.

For the solution of the differential equation:

y(t) = A sin(ωt + φ)

dy/dt = Aω cos(ωt + φ)

d²y/dt = -Aω² sin(ωt + φ)

Put these equations in the differential equation

d²y/dt² + (k/m) y = 0

-Aω² sin(ωt + φ) + (k/m)A sin(ωt + φ)

ω² = (k/m) ⇒ ω = √(k/m)

Therefore,

y(t) = A sin(ωt + φ)

v(t) = Aω cos(ωt + φ)

a(t) = -Aω² sin(ωt + φ)

a(t) = -ω²y(t)

Where, ω² = (k/m) ⇒ ω = √(k/m)

Also check - Darwin’s Research On Worms: Tiniest But Rather Important Creatures

Energy In Harmonic Motion

Another crucial aspect of harmonic motion is its energy dynamics. In an idealised system with no damping or external forces, the total mechanical energy of the system remains constant. The energy is shared between kinetic energy (KE) and potential energy (PE).

The kinetic energy can be expressed as:

KE = (1/2) m v²

And the potential energy as:

PE = (1/2) k x²

The total mechanical energy E is given by the sum of KE and PE:

E = KE + PE = (1/2) m v² + (1/2) k x²

E = KE + PE = (1/2) m (dx/dt)² + (1/2) k x²

This constant energy is an essential property of SHM and can be used to analyse and understand the motion of oscillating systems.

Simple Angular Harmonic Motion

Angular Simple Harmonic Motion occurs when a system undergoes angular oscillations around a fixed axis. In this type of motion, the displacement of the particle is measured in terms of angular displacement. One classic example of Angular SHM is the motion of a torsional pendulum.

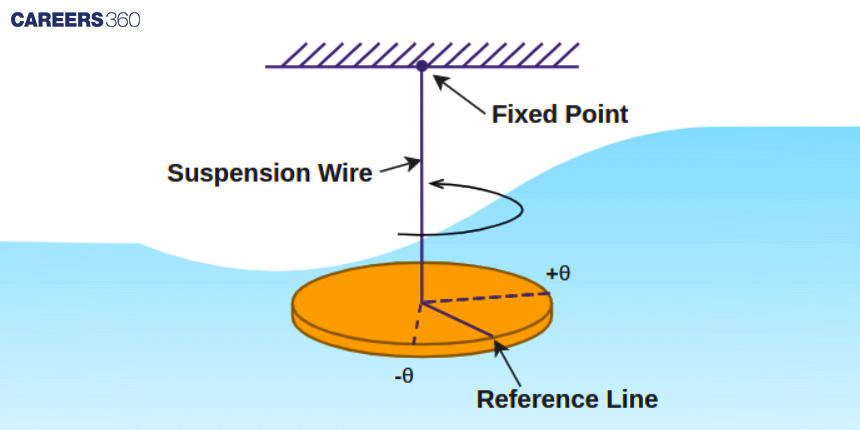
For Angular Simple Harmonic Motion to occur, certain conditions must be met. The restoring torque (or angular acceleration) acting on the particle must always be directly proportional to the particle's angular displacement and must be oriented toward the equilibrium position.

In mathematical terms,

T ∝ -θ

α ∝ -θ

where:

T represents Torque, θ represents Angular Displacement, and α represents the Angular Acceleration.

Differential equations for the angular harmonic motion:

τ = -kθ, where k is a torsional coefficient.

We know that τ = Iα

Where I is a moment of inertial and is angular acceleration.

Iα = -kθ

α = -(k/I)θ

d²θ/dt² = -(k/I)θ

Solution of differential equation is given as

θ = θ₀sin(ωt + φ)

Where, ω² = (k/I) ⇒ ω = √(k/I)

NCERT Chapters Required Harmonic Motion Concepts

National Council of Educational Research and Training (NCERT) textbooks for Class 11 and 12, harmonic motion concepts are primarily covered in the following chapters:

Class 11 Physics

• Chapter 14: Oscillations

This chapter provides an introduction to oscillatory motion and harmonic oscillators. It covers simple harmonic motion, the spring-mass system, and the mathematical representation of oscillations using differential equations.

Class 12 Physics

• Chapter 3: Current Electricity

While this chapter mainly deals with electric circuits, it briefly discusses the concepts of LCR (Inductor-Resistor-Capacitor) circuits, which exhibit harmonic oscillations in alternating current (AC) circuits.

• Chapter 7: Alternating Current

This chapter delves deeper into AC circuits and discusses LCR circuits' resonance phenomenon, which involves harmonic motion principles.

• Chapter 14: Semiconductor Electronics: Materials, Devices, and Simple Circuits

This chapter introduces the concept of electronic devices, such as diodes and transistors, which can generate and amplify electrical oscillations.

Examples Of Simple Harmonic Motion

SHM is prevalent in everyday life, and numerous examples can be observed around us. Some common examples include

• Swings in a Park: The motion of a swing back and forth is a classic example of SHM.

• Pendulum Motion: The motion of a simple pendulum, such as a grandfather clock, also follows SHM if the amplitude of its swing is small.

• Vibrations of Musical Instruments: The strings of musical instruments like the guitar and violin vibrate in SHM, producing pleasing sounds.

• Membrane Vibrations: The vibrations of the membrane in drums and diaphragms in telephones and speaker systems create precise sound.

Also check - Cricket's Sweet Spot: Understanding The Physics Of Bat-Ball Collisions

Importance Of Understanding Harmonic Motion For Students

>>> Scoring well in Physics and Mathematics: A solid grasp of harmonic motion concepts can significantly impact a student's performance in physics and mathematics. Many exam boards, including CBSE and State boards, include harmonic motion in their syllabus for classes 11th and 12th. Moreover, questions related to this topic frequently appear in board exams. By understanding the underlying mathematics and physics, students can confidently approach these questions and score well.

>>> Excel in Competitive Exams: For students aspiring to pursue careers in engineering (JEE) or medical (NEET) fields, a profound understanding of harmonic motion is invaluable. These competitive exams often have challenging questions that test students' analytical and problem-solving abilities. Harmonic motion-based problems can be used to evaluate a student's grasp of differential equations and their application in real-world scenarios.

>>> Interdisciplinary Applications: Harmonic motion is not limited to physics alone; it has applications in various interdisciplinary fields. In engineering, harmonic motion principles are crucial in understanding vibrations and resonance phenomena. In music, harmonics are essential in the study of sound waves and musical instruments. Even biological systems, such as the human heart's oscillatory motion, can be analysed using similar mathematical principles.