Differential Equations And Motion Of A Space Vehicle

Motion of a space vehicle is a complex phenomenon that can be studied and analysed using the principles of calculus and differential equations. In Class 12 mathematics, students learn about these concepts and their application in the study of motion.

Differential equations are encountered in a wide range of fields including Physics, Chemistry, Biology, Anthropology, Geology, Economics, and others. These equations are used to model physical phenomena and can provide information about the rate of change of a particular quantity. In the case of motion, differential equations can be used to describe the position, velocity, and acceleration of a space vehicle.

One common type of differential equation used in the study of motion is the second-order differential equation. This type of equation provides information about the acceleration of a space vehicle, given its position and velocity. The equation is derived from Newton's second law of motion, which states that the acceleration of an object is proportional to the force acting on it. The following image shows the thrust provided by a rocket to launch a space vehicle.

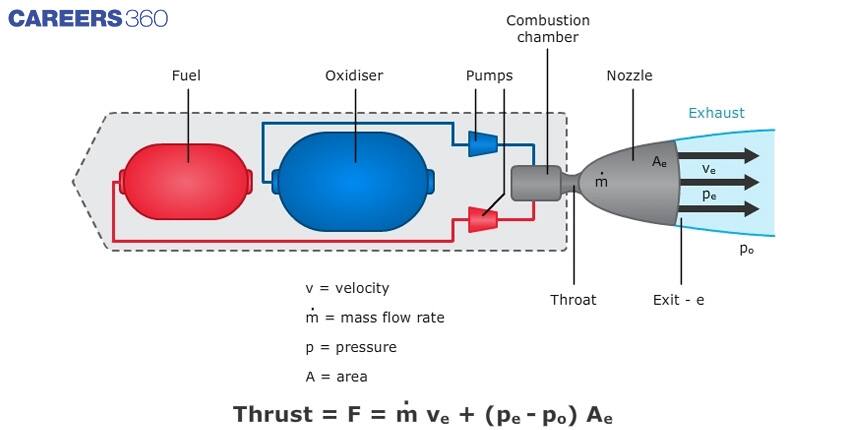
A differential equation for rocket motion is given as

F = ( dm / dt ) V_e + ( P_e - P_o ) A_e

Where

dm/dt = Mass flow rate

V_e = Exit velocity, P_e = Exit Pressure, P_o = Outside pressure, A_e = Nozzle exit area

Another important aspect of the motion of a space vehicle is the influence of external forces, such as gravity, air resistance, and propulsion. These forces can be incorporated into the differential equation to provide a more accurate model of the motion. To understand motion in space we vector representation of position, velocity, and acceleration.

The position vector is given as r = x i + y j + z k

Velocity can be given as v = dr / dt

Acceleration is given as a = d²r / dt²

Also check - Factors That Affect The Longevity Of Life

Orbital Motion Of A Space Vehicle

The orbital motion of a space vehicle can be described using differential equations. The position and velocity of the spacecraft can be modelled as functions of time. The acceleration of the spacecraft is determined by the forces acting on it, including gravity, thrust, drag, and atmospheric resistance. These forces can be represented mathematically as vectors and can be used to write a set of differential equations that describe the motion of the spacecraft. For example, in two dimensions, the position of the spacecraft can be described by two differential equations:

dx / dt= V_x and dy / dt = V_y

where x and y are the coordinates of the spacecraft and V_x and V_y are its velocity components in the x and y directions, respectively. The velocity of the spacecraft can be described by another set of differential equations:

d²x/dt² = dV_x/dt = a_x and d²y / dt² = dV_y / dt = a_y

where ax and ay are the acceleration components of the spacecraft in the x and y directions, respectively. The acceleration is determined by the forces acting on the spacecraft and can be calculated using Newton's laws of motion.

In addition to describing the motion of a space vehicle, differential equations can also be used to find the maximum and minimum values of quantities, such as the maximum height reached by spacecraft or the minimum energy required for a spacecraft to reach a particular destination. These concepts are important for the design and optimization of space missions. For example Indian Space Research Organisation (ISRO) used the Hohmann transfer orbit concept for its Mars Orbiter Mission (MOM), also known as Mangalyaan.

The Hohmann transfer orbit is a method of transferring a spacecraft from one circular orbit to another using a minimum amount of energy. It involves calculating the velocity changes required to move the spacecraft from its initial orbit to a transfer orbit that intersects with the target orbit. The spacecraft then makes a second burn to enter the target orbit.

ISRO used this concept to transfer the Mars Orbiter Mission spacecraft from its initial Earth orbit to a transfer orbit that intersected with Mars' orbit. The spacecraft then performed a second burn to enter into Mars orbit. By using the Hohmann transfer concept, ISRO was able to save fuel and minimise the energy required for the mission.

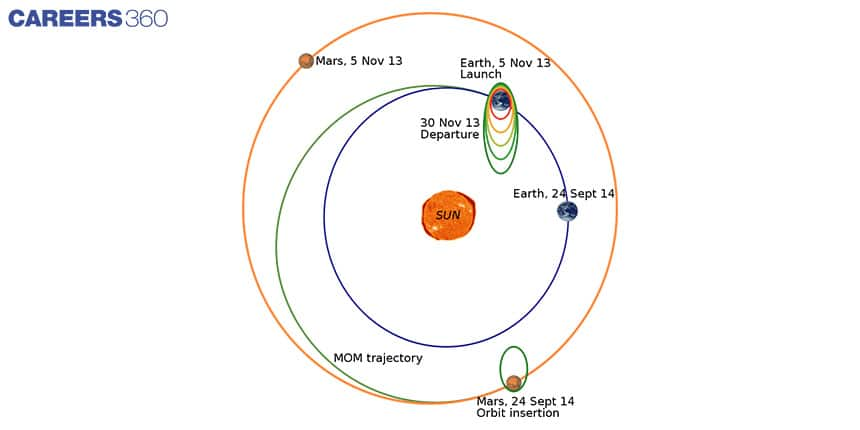
The above image shows the Mars Orbiter Mission (MOM) launched by Indian Space Research Organisation (ISRO) in 2013.

Also check - What Is The Physics Behind Death Well?