Bihar Board 10th Math Question Paper 2025 (18 Feb): Objective & Subjective Questions Analysis

Bihar School Examination Board (BSEB) is responsible for conducting matrics and intermediate examinations across the state. The Bihar board class 10 examination started on 17 February with two shifts (morning and evening), which will conclude on 25 February 2025.

The Bihar board class 10 mathematics (subject code- 110) examination is scheduled for 18 February (Tuesday), today in both the shifts from 9:30 am to 12:45 pm and 2:00 pm to 5:15 pm, respectively. The Bihar board matric mathematics examination 2025 both morning and evening shifts is over now. The level of difficulty of the Bihar board class 10 mathematics exam was moderate. Arithmetic Progression questions were dominating in the paper. Download the Bihar board class 10 maths question paper, answer key with details explanation and details analysis of BSEB matric maths exam 2025 scoring down to this page.

Bihar Board Class 10 Mathematics Exam 2025 Overview

Below is the Bihar Board matric examination overview, which contains exam information, the number of questions, and all the necessary details.

BSEB Class 10 Math Exam 2025 Analysis

The BSEB Class 10 Mathematics Exam 2025 was moderate-level, with almost 45% of the questions requiring two-step calculations and formula application.

Let's have a look at the level of difficulty of secondary school examination 2025 math from the table given below:

The stacked bar chart below represents the number of questions asked in the BSEB Class 10 Mathematics Examination 2025, categorized by difficulty levels across different topics.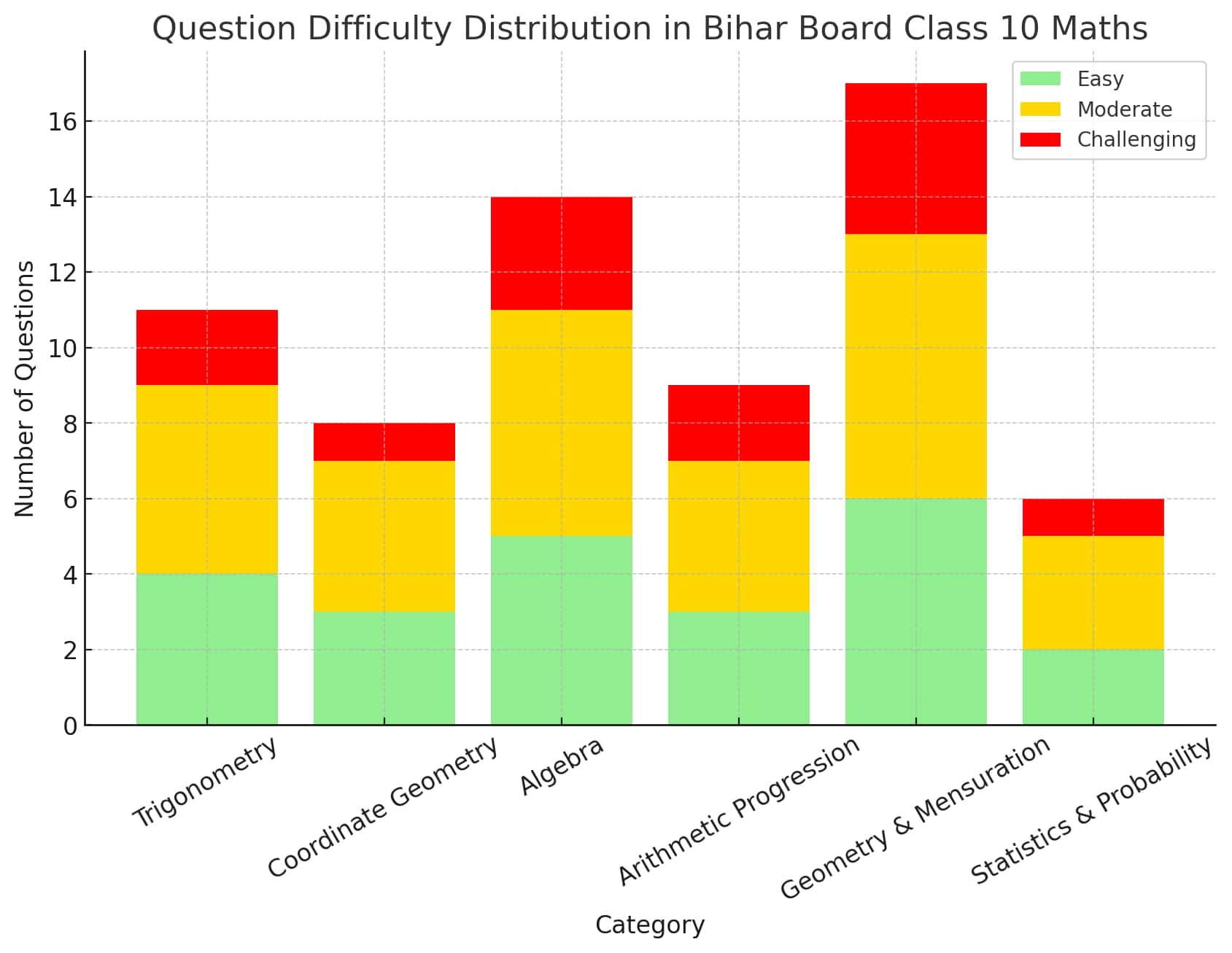

Bihar Board Class 10 Mathematics Question Paper 2025

BSEB secondary school examination 2025 math is successfully over for shift 1 now. Click on the link below to download the BSEB class 10 maths question paper PDF 2025.

Question 1. $\sin ({90}^{\circ }-A)=\cos A$
(A) $\sin A$
(B) $\cos A$
(C) $\tan A$
(D) $\sec A$

Question 2. If $\alpha =\beta ={60}^{\circ }$ then the value of $\cos (\alpha -\beta )$ is
(A) $\frac{1}{2}$
(B) 1
(C) 0
(D) 2

Question 3. If $\theta ={45}^{\circ }$ then the value of $\sin \theta +\cos \theta$ is
(A) $\frac{1}{\sqrt{2}}$
(B) $\sqrt{2}$
(C) $\frac{1}{2}$
(D) 1

Question 4. If $A={30}^{\circ }$ then the value of $\frac{2\tan A}{1-{\tan }^{2}A}$ is
(A) $2\tan {30}^{\circ }$
(B) $\tan {60}^{\circ }$
(C) $2\tan {60}^{\circ }$
(D) $\tan {30}^{\circ }$

Question 5. If $\tan \theta =\frac{12}{5}$ then the value of $\sin \theta$ is
(A) $\frac{5}{12}$

(B) $\frac{12}{13}$
(C) $\frac{5}{13}$
(D) $\frac{12}{5}$

Question 6. $\frac{\cos {59}^{\circ }}{\sin {31}^{\circ }}\times \frac{\tan {80}^{\circ }}{\cot {10}^{\circ }}=$

(A) $\frac{1}{\sqrt{2}}$

(B) 1
(C) $\frac{\sqrt{3}}{2}$
(D) $\frac{1}{2}$

Question 7. If $\tan {25}^{\circ }\times \tan {65}^{\circ }=\sin A$ then the value of $A$ is
(A) ${25}^{\circ }$
(B) ${65}^{\circ }$
(C) ${90}^{\circ }$
(D) ${45}^{\circ }$

Question 8. If $\cos \theta =x$ then $\tan \theta =$
(A) $\frac{\sqrt{1+x^2}}{x}$
(1) $\frac{\sqrt{1-x^2}}{x}$
(C) $\sqrt{1-x^2}$
(D) $\frac{x}{\sqrt{1-x^2}}$

Question 9. $(1-{\cos }^4\theta )=$
(A) ${\cos }^2\theta (1-{\cos }^2\theta )$
(B4) ${\sin }^2\theta (1+{\cos }^2\theta )$
(C) ${\sin }^2\theta (1-{\sin }^2\theta )$.
(D) ${\sin }^2\theta (1+{\sin }^{2}0)$

Question 10. What is the form of a point lying on $y$-axis ?
(A) $(y,0)$
(B) $(2,y)$
(C) $(0,x)$
(D) None of these

Bihar Board Matric Mathematics Question Paper Previous Year

Check the Bihar Board Matric previous year's question paper, which is one of the essential resources to score good marks in future Bihar Board matric exams.

Bihar Board Class 10 Mathematics Answer Key 2025

Bihar Board class 10 maths shift 1 paper was concluded and shift 2 is going according to the scheduled time. Bihar Board class 10 mathematics Answer key of question paper set F is given below.

BSEB Class 10 Maths Solution 2025: Section-A

(Q1)

We use the complementary angle identity of trigonometry:

$\sin ({90}^{\circ }-A)=\cos A$

Comparing with the given expression, we see that:

$\sin ({90}^{\circ }-A)=\cos A$

Hence, the answer is the option (2).

(Q2.)

Given:

$\alpha =\beta ={60}^{\circ }$

We use the trigonometric identity:

$\cos (\alpha -\beta )=\cos 0^{\circ }$

Since $\cos 0^{\circ }=1$, we get:

$\cos ({60}^{\circ }-{60}^{\circ })=\cos 0^{\circ }=1$
Hence, the answer is the option (2).

(Q3.)

Given:

$\theta ={45}^{\circ }$

We calculate:

$\sin {45}^{\circ }+\cos {45}^{\circ }$

Since,

$\sin {45}^{\circ }=\frac{1}{\sqrt{2}},\cos {45}^{\circ }=\frac{1}{\sqrt{2}}$

Adding these values,

$\sin {45}^{\circ }+\cos {45}^{\circ }=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$
Hence, the answer is the option (2),

Ans.4)

We need to evaluate:

$\frac{2\tan A}{1-{\tan }^{2}A}$

Given $A={30}^{\circ }$, we substitute $\tan {30}^{\circ }=\frac{1}{\sqrt{3}}$ :

$\frac{2\times \frac{1}{\sqrt{3}}}{1-{\left(\frac{1}{\sqrt{3}}\right)}^2}$

Calculating the denominator:

$1-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}=\frac{2}{3}$

Thus,

$\frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}}=\frac{2}{\sqrt{3}}\times \frac{3}{2}=\frac{6}{2\sqrt{3}}=\frac{3}{\sqrt{3}}=\sqrt{3}$

Since $\tan {60}^{\circ }=\sqrt{3}$, we conclude:

$\frac{2\tan {30}^{\circ }}{1-{\tan }^2{30}^{\circ }}=\tan {60}^{\circ }$
Hence, the answer is the option (2).

Ans.5)

We are given:

$\tan \theta =\frac{12}{5}$

Using the identity:

$\tan \theta =\frac{\sin \theta }{\cos \theta }$

we consider a right-angled triangle where the opposite side is 12 and the adjacent side is 5 . Using the Pythagorean theorem, the hypotenuse is:

$r=\sqrt{{12}^2+5^2}=\sqrt{144+25}=\sqrt{169}=13$

Hence, the answer is the option (2).

Ans 6)

We simplify the given expression:

$\frac{\cos {59}^{\circ }}{\sin {31}^{\circ }}\times \frac{\tan {80}^{\circ }}{\cot {10}^{\circ }}$

Using Complementary Angle Identities
We know that:

$\cos {59}^{\circ }=\sin ({90}^{\circ }-{59}^{\circ })=\sin {31}^{\circ }$

Thus,

$\frac{\tan {80}^{\circ }}{\cot {10}^{\circ }}=\tan {80}^{\circ }\times \tan {10}^{\circ }$

Using the identity:

$\tan ({90}^{\circ }-x)=\cot x$

we get:

$\tan {80}^{\circ }=\cot {10}^{\circ }$

So,

$\tan {80}^{\circ }\times \tan {10}^{\circ }=\cot {10}^{\circ }\times \tan {10}^{\circ }=1$

Hence, the answer is the option (2).

Ans.7)

We are given:

$\tan {25}^{\circ }\times \tan {65}^{\circ }=\sin A$
We know that:

$\tan ({90}^{\circ }-x)=\cot x$

Thus,

$\tan {65}^{\circ }=\cot {25}^{\circ }$

$A={90}^{\circ }$

Hence, the answer is the option (3).

Ans.8)

We are given:

$\cos \theta =x$
From the fundamental identity of trigonometry:

${\sin }^2\theta +{\cos }^2\theta =1$

Substituting $\cos \theta =x$ :

$\begin{array}{rl}& {\sin }^2\theta +x^2=1\\ & {\sin }^2\theta =1-x^2\\ & \sin \theta =\sqrt{1-x^2}\end{array}$
We use the definition of tangent:

$\tan \theta =\frac{\sin \theta }{\cos \theta }$

Substituting values:

$\tan \theta =\frac{\sqrt{1-x^2}}{x}$
Hence, the answer is the option (2).

Ans.9)

We start with the given expression:

$1-{\cos }^4\theta$
We use the identity:

$a^2-b^2=(a-b)(a+b)$

Rewriting ${\cos }^4\theta$ as ${({\cos }^2\theta )}^2$, we get:

$1-{\cos }^4\theta =(1-{\cos }^2\theta )(1+{\cos }^2\theta )$

Hence, the answer is the option (2).

Ans.10)

A point lying on the $y$-axis means that its $x$-coordinate is always 0 because any point on the $y$-axis has no horizontal displacement.

Thus, the general form of a point on the $y$-axis is:

$(0,y)$
Hence, the answer is the option (3).

To access the complete Bihar board class 10 mathematics answer key with a proper explanation, click on the link below, which is free of charge.